2064

На рис. 1.6 кривая 4 характеризует эффективность размерной селекции ППФ последнего типа и определяется суммой кривых типа 1, построенных для разноразмерных объектов. По сравнению со схемой на рис. 1.5, б обеспечиваемое отношение сигнал/помеха выше, и ППФ такой структуры следует рекомендовать для обнаружения слабоконтрастных объектов.

Фильтры на рис. 1.5 выполняют функцию не только обнаружения сигнала. Они реагируют на изображения пятен с круговой симметрией и подавляют другие виды сигналов. Отсюда можно сделать вывод, что алгоритм опознавания может строиться на синтезе совокупности обнаружителей рассмотренного вида, каждый из которых реагирует на сигналы определенного класса.

нормальным распределением, характеризуемым нулевым средним значением и дисперсией 2 . Метод обнаружения – однократный отсчет, цены ошибок равны, априорная вероятность появления сигнала – 0,5.

Требуется установить порог принятия решений.

Решение

Плотность распределения помехи и суммы сигнала и помехи соответственно записываются для сформулированной задачи в виде

Байесово правило при заданных априорных вероятностях и ценах ошибок дает ΒΠ ΔΒс /2. При применении критерия Неймана-Пирсона порог принятия решений находится из уравнения

p0 Βш dΒ ε ,

ΒΠ

21

решение которого через функцию Лапласа

имеет вид

Рис. 1.7. Зависимость относительного порога от ошибки первого рода

2. Построить фильтр, согласованный с прямоугольным импульсом амплитудой Вс и длительностью . Оценить отношение сигнал/шум на его выходе.

Решение

Будем рассматривать сигнал, симметричный относительно среднего положения, т.е.

22

Необходимо подобрать такую линейную систему, импульсная характеристика которой представляла бы собой прямоугольный видеоимпульс. Известно, что при действии единичного импульса на вход интегрирующего устройства на его выходе образуется скачок напряжения в виде единичной функции t . Прямоугольный импульс единичной амплитуды и длительности представляет собой разность единичных функций t и t-τ , смещенных относительно друг друга на время τ . Поэтому линейной системой, импульсная характеристика которой описывается прямоугольным импульсом, может служить схема, представленная на рис. 1.8, а, содержащая интегратор 1, линию задержки 2, вычитающее устройство 3. Временные диаграммы работы этой системы при действии на её вход единичного импульса изображены на рис. 1.8,

б-г.

Переходная характеристика интегрирующего устройства

При воздействии на его вход прямоугольного сигнала выходное напряжение интегратора будет изменяться по закону

,

а с учетом линии задержки

t u .

23

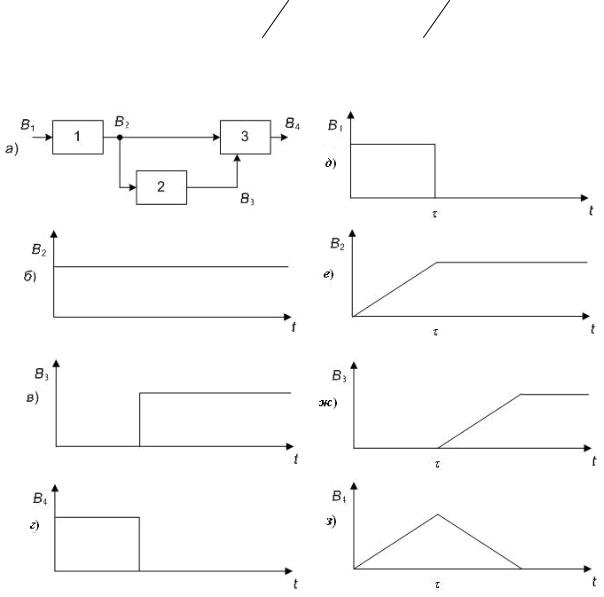
После прохождения линии задержки это колебание запоздает на время (рис. 1.8, ж). На выходе вычитающего устройства сформируется импульс приблизительно треугольной формы (рис. 1.8, з).

0 t ;

Рис. 1.8. Структурная схема согласованного фильтра для прямоугольного

сигнала (а); временные диаграммы его работы при входных воздействиях:

единичный импульс (б – г); прямоугольный импульс (д – з)

24

длительность, приближенно равную 2 .

Для вычисления мощности шума на выходе интегрирующего устройства воспользуемся формулой для автокорреляционной функции:

Отсюда следует, что шум на выходе интегрирующего устройства имеет мощность

22 K2 0 Nш u .

4

25

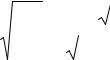
Колебание с выхода интегрирующего устройства поступает непосредственно на вычитающее устройство и с задержкой на :

B4 t B2 t B3 t B2 t B2 t .

Поэтому мощность выходного шума

42 m1 B42 m1 B4 2 m1 B22 t m1B22 t

2m1 B2 t B2 t .

Для стационарного шума

Искомое отношение сигнал/шум на выходе фильтра

Контрольные вопросы

1.Что характеризует отношение правдоподобия?

2.Какой случайный процесс называют стационарным?

3.Правило Неймана-Пирсона.

4.Правило минимакса (минимаксный критерий).

5.Какие фильтры называют согласованными?

6.Какие фильтры называют оптимальными?

2.ЗАДАЧА РАСПОЗНАВАНИЯ ОБРАЗОВ

Впоследние годы в России и за рубежом все большее значение приобретает защита от несанкционированного доступа к различным

26

физическим объектам и информационным ресурсам. Основным способом решения этой проблемы является идентификация личности, основанная как на использовании кодовых слов (паролей, ключей) или карт доступа, так и биометрических характеристик человека. В последнем случае мы имеем дело с задачей классификации субъектов (объектов).

Известно, что под терминами классификация и идентификация понимают разбиение совокупности объектов (субъектов) на группы. Переход от массива данных, характеризующих объект (субъект), к более «лаконичному» его описанию с минимальной потерей полезной информации составляет сущность процесса снижения размерности. Оба введенных термина используются в математической статистике. В технической литературе вместо термина «классификация объектов» используют термин распознавание образов или идентификация объектов; для «лаконичного» описания объектов применение нашел термин «признаки», а процедура снижения размерности названа «формированием пространства признаков».

При решении практических задач необходимо не только обнаружить объекты, но и классифицировать (распознать) их. В самом общем виде задача распознавания предусматривает выделение объектов, принадлежащих одному классу, из множества объектов, относящихся к разным классам. Под классом объектов понимается совокупность образов – элементов класса, обладающая набором идентичных характеристик. Эти характеристики, позволяющие отличить классы друг от друга, называются признаками. При разделении двух классов приходим к задаче обнаружения.

При разработке систем распознавания решают, как правило, триединую задачу. Прежде всего необходимо выбрать признаки, по совокупности которых проводится классификация. Если признак один, на шкале устанавливаются границы отрезков, определяющих области классов. Для двух признаков каждый класс характеризуется областью на плоскости, при большем числе признаков каждый объект определяется точкой в многомерном пространстве. Множество таких точек, относящихся к одному классу образов, представляющее в пространстве признаков компактную (выделяющуюся) область, принято называть кластером. Проблему выбора признаков поясняет рис. 2.1.

27

Рис. 2.1. Иллюстрация проблемы выбора признаков при распознавании образов: а – случай сильнокоррелируемых признаков x1i и x2i ;

б – случай использования неэффективного признака x1i

Допустим, что необходимо построить алгоритм для распознавания трех классов i =1, 2, 3. Опытный аналитик рекомендует использовать для решения задачи два признака классов x1i и x2i . В процессе экспериментальных исследований выясняется, что признаки для группы объектов каждого класса

точки векторов, описаний объектов каждого класса. Но тот же эффект по разделению классов объектов будет достигнут, если использовать информацию о значении одного признака. Второй будет избыточен и его включение в алгоритм не даст повышение надежности распознавания.

Вторую сторону вопроса выбора признаков отражает рис. 2.1, б. Области классов, формируемые признаком x1i , перекрываются, и его использование для решения задачи разделения классов не продуктивно.

Обобщая случаи формирования областей классов на рис.2.1,

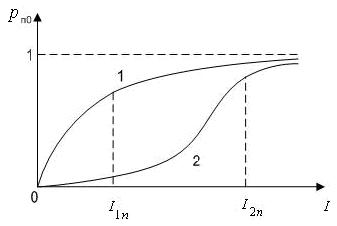
(полноты описания объектов) изменяется в соответствии с кривой, расположенной между сплошными кривыми 1, 2 (рис. 2.2).

Рис. 2.2. Варианты зависимостей вероятности правильного распознавания объектов от полноты описания (числа признаков)

Кривая 1 отражает наилучший случай, когда использование очередного признака дает максимальный прирост dpn /dI , чем достигается максимальная экономия ресурсов распознающего автомата. При необходимости увеличения pn(pn pn(I1n)) потребуется значительное приращение ресурсов dI : автомат работает с менее информативными или коррелированными признаками.

В наиболее неблагоприятном случае (кривая 2) процедура распознавания объектов начинается с использования малоинформативных признаков. Поэтому достичь сходных результатов pn(I1n) pn(I2n) удается при существенном увеличении ресурсов машины (I2n I1n ), направленных на достижение поставленной цели. Отсюда следует вторая задача распознавания образов – проранжировать признаки по

распознавания.

Третья задача состоит в отыскании решающей процедуры, позволяющей классифицировать распознаваемые образы. При наличии m классов пространство признаков состоит из m областей, каждая из которых содержит точки, соответствующие

29

образам одного класса. Тогда построение решающей процедуры сводится к построению границ областей, разделяющих классы.

Для построения границ областей вводится этап обучения, на котором системе предъявляется множество образов, относящихся к известным классам. Считается, что число образов, предъявляемых на этапе обучения, может быть ограничено 20n, где n – число признаков.

На этапе распознавания системе предъявляется неизвестный образ. Если его описание попадает в одну из построенных на этапе обучения областей, процесс распознавания сводится к установлению этого факта и вынесению заключения об отнесении объекта к найденному классу.

Базовой технологией этапа распознавания образов считается байесова процедура (стратегия) принятия решений. Пусть, например, требуется разделить объекты на классы Н1 и Н2 по одному признаку x.

Имеем дело с задачей обнаружения, рассмотренной выше. Некоторое усложнение ее связано с использованием матрицы стоимости решений

C C11 C12 ,

C21 C22

оптимального порога принятия решений x0.

30