Лабораторная работа № 6

СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ПРОЦЕССОВ

Цель работы: получить навыки работы по спектральному представлению исследуемых процессов.

Краткие сведения из теории сигналов

Любое колебание f(t) можно представить в виде комбинации составляющих φi(t) путем их подбора и взвешивания через коэффициенты Сi так, чтобы

N

f(t) = ∑Ci φi(t),

i =1

или путем разложения его по упорядоченной системе ортогональных функций С1(t), С2(t), …, Сm(t). Эти функции должны удовлетворять на некотором отрезке времени (t1, t2) условиям

t2

(t2 −t1)−1 ∫Ci (t) Ck (t)dt = 0,·

t1

где i=1,2,…, m; k=1,2,…, m и i≠k.

Если обозначенные функции удовлетворяют также условию

b∫2 Ci2 (t)dt =1,

b1

то систему называют ортонормированной.

Простейшим примером ортогональных колебаний являются sin ωit и cos ωkt, где ω = 2π/Т – частота колебаний; Т – период колебания. Заданное (аналитически или графически) колебание можно разложить по системе ортогональных функций f(t) ≈ ∑ai Ci (t) и при ко-

i

нечном числе членов в ряде разница между f(t) и ∑ai Ci (t) будет дос-

i

таточно мала, т.е.

будет минимально возможной, если коэффициенты ai определяются по формуле

+Т

ai = ∫∫ f (t) Ci (t)dt ,

−Т

где 2Т – временной интервал представления функции f(t).

Интегралы берутся по области задания процесса, которая должна находиться внутри отрезка ортогональности.

Среди систем функций, обладающих свойством ортогональности на различных отрезках, применение находят тригонометрические функции кратных аргументов, полиномы Эрмита, Лежандра, Чебыше- ва–Лагерра, Уолша, Хаара и др.

При использовании тригонометрических функций процесс записывается в виде

k =∞

где 2Сk = Сk exp (–jφk) = ak – jbk; Сk = 2|Сk|; C0 = C0.

Величина 2Сk есть комплексная амплитуда

Учитывая, что вещественная часть каждого слагаемого под знаком суммы в формуле (6.2) четна по отношению к k , мнимая – нечетна, можно от формулы (6.2) перейти к формуле (6.1).

Ряд Фурье (6.1), (6.2) характеризует представление периодической функции суммой тригонометрических функций. Непериодическую функцию можно рассматривать как предельный случай периодической функции при неограниченно возрастающем периоде.

Подставив формулу (6.3) в (6.2), получим

При Т→∞ ω1 = (2π /Т)→dω; (2πk /Т)→ω, где ω – текущая частота; dω – ее приращение.

Сумма перейдет в интеграл

−∞

Формулы (6.4) и (6.5) являются основными формулами теории спектров. Они представляют собой пару преобразований, связывающих вещественную функцию времени f(t) и комплексную функцию частоты S(ω). Смысл формулы (6.4) состоит в том, что f(t) представлена суммой бесконечного числа синусоидальных составляющих, бесконечно близких по частоте.

Таким образом, ряд Фурье представляет периодическую функцию как сумму периодических составляющих, тогда как интеграл Фурье представляет непериодическую функцию как сумму периодических составляющих.

Перейдем к рассмотрению спектральных представлений случайных процессов.

Если в формуле (6.5) заменить детерминированную функцию f(t) случайным процессом ξ(t), то полученная функция S(ω) будет отражать спектральную плотность одной реализации этого процесса.

Чтобы получить спектр случайного процесса, предложено вместо функции f(t) в формуле (6.5) использовать функцию корреляции R(τ):

Учитывая, что функции R(τ) и G(ω) – частота функции своих аргументов, они могут быть представлены в вещественной форме

Для спектров случайных процессов и их функций корреляции имеет место соотношение f·rk ≈ 1, где f = ω /2π; f – ширина спектра частот между нулем и тем значением частоты, когда спектральная функция G(ω) первый раз обращается в нуль.

Задание

1.Изучите теоретическую часть.

2.Запрограммируйте генерацию двух гармонических сигналов заданной частоты (частота – произвольная) и их отображение на двух графиках.

3.Реализуйте сигнал, равный сумме двух гармонических сигналов, сгенерированных по п. 2.

4.Реализуйте операцию получения спектра суммарного сигнала. Изобразите результаты выполнения пп. 2–4 в виде графиков, представленных на рис. 6.1.

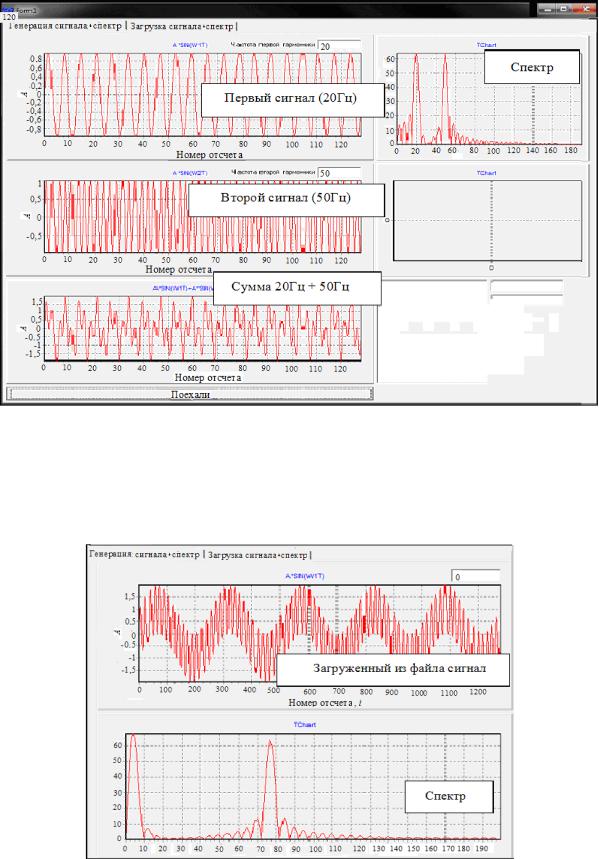
Рис. 6.1. Генерация двух сигналов, их сумма и спектр

5. Выполните загрузку файла с сигналом (1280 точек), выданным преподавателем (по вариантам), постройте графики функции и ее спектры в форме, представленной на рис. 6.2.

Рис. 6.2. Загрузка файла с индивидуальным сигналом и его разложение в спектр (гармоники 5 и 78 Гц)

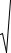
6. Получите результаты перехода от корреляционных функций R(τ) к спектральным плотностям G(ω) по формулам (6.6), (6.8), если

R4(τ) = cos ω0τ ; R5(τ) = [1 + α|τ|) + 13 (ατ)2] e-α|τ| ;

R6(τ) = 1 + α|τ| – 2(ατ)2 + 13 [α|τ|3] e-α|τ| ;

R7(τ) = [1 + (ατ)2]-1; R8(τ) = sech (ατ).

Постройте графики Ri (τ) и соответствующие им Gi(ω).

7. Сопоставьте полученные результаты Gi(ω) со следующими спектральными плотностями GiТ (ω) (эталонами):

По результатам сопоставления сделайте вывод, к какому из представленных выводов GiТ(ω) относится каждый из полученных Gi(ω).

Содержание отчета

1.Цель работы.

2.Изображения с сигналами S1, S2 и S3 = S2 + S1 с выбранными вами частотами (от 0 до 100 Гц) и описанием.

3.Изображение разложения сигнала S3 в спектр с текстовым описанием к нему.

4.Изображение графика сигнала, выданного преподавателем (по вариантам), и описанием к нему.

5.Изображение с разложением выданного сигнала в спектр и описанием графика.

6.Исходный код программы.

7.Выводы о зафиксированных гармониках в сигнале.

8.Выводы по результатам выполнения пп. 6 и 7 задания.

Порядок выполнения работы

1.Создаем новый проект в C++ Builder (в данном примере ис-

пользовался C++ Builder XE).

2.Помещаем необходимые элементы на форму, как указано на

рис. 6.3.

Рис. 6.3. Изображение элементов интерфейса

3. В обработчике события нажатием кнопки необходимо прописать генерацию трех сигналов по формуле (6.1).

Пример генерации с временным шагом (частота дискретизации)

1/1280:

for (float i=0;i<128;i=i+0.1)

{

aa[ii] = sin(2*3.14*i/128*f1); // генерация первой гармоники bb[ii] = sin(2*3.14*i/128*f2); // генерация второй гармоники

SS[ii] = aa[ii]+bb[ii]; // генерация суммы двух колебаний

Form1->Series1->AddXY(i,aa[ii]); // отображение первой синусоиды Form1->Series2->AddXY(i,bb[ii]); // отображение второй синусоиды Form1->Series3->AddXY(i,SS[ii]); // отражение суммарного сигнала ii+=1;

}

В приведенном примере осуществляется построение синусоиды частотой f1 и f2 из 1280 точек с шагом в 1/1280 и суммарный сигнал.

4. Для построения спектра необходимо умножать каждую точку исходного сигнала на каждую точку синусоиды с частотой от 1 до 100 Гц и накапливать сумму этих произведений. Иными словами, построение спектра с помощью ДПФ – это умножение исходного сигнала на синусоиды частотами 1,2,3…100 Гц (или более, если необходимо) и фиксирование (откладывание на графике спектра) значения суммы произведений. Если исходный сигнал совпадет с искомой синусоидой, то сумма произведений окажется значительной и на графике появится ярко выраженный пик, что покажет наличие синусоиды соответствующей частоты.

Построение спектра реализуется с помощью формулы

S = S + SS[ii]*sin(2*3.14*j*i/1280), где j – перебираемая частота си-

нусоиды (от 1 до 100), SS[ii] – точка исходного сигнала, i/1280 – временной чаг (дискретизация); S – сумма в накопителе, откладываемая на графике спектра попарно с j. S необходимо брать по модулю. Перебираем все значения i и производим умножение. Затем увеличиваем j на единицу и повторяем цикл нахождения суммы произведений, пока

строения спектра. Установить необходимые компоненты, как указано на рис. 6.4.

6. Поместить выданный преподавателем файл .txt с сигналом в папку с проектом и загрузить сигнал в компонент Memo с помощью следующей строки кода:

Memo2->Lines->LoadFromFile("название.txt");

Рис. 6.4. Графики для построения спектра

7.Для обращения к данным из компоненты Memo2 и построения графика сигнала следует использовать код (в файле 1280 значений): for (int i = 0; i < Memo2->Lines->Count; i++)

LineSeries1->AddXY(i,StrToFloat(Memo2->Lines->Strings[i]));

8.Построить спектр сигнала, обращаясь к элементам компоненты Memo2, как указано в п. 4.

Контрольные вопросы

1. В чем заключается принцип дискретного преобразования Фу-

рье?

2.Каким образом осуществляется обратное преобразование Фурье для получения исходного сигнала?

3.В чем принципиальное отличие спектров случайного и детерминированного процессов?