
Лабораторная работа № 2
АНАЛИЗ КАЧЕСТВА ГСПЧ
Цель работы: проанализировать равномерность распределения и статистическую независимость чисел на выходе ГСПЧ.
Краткие сведения из теории построения ГСПЧ
Для анализа качества ГСПЧ применяются различные статистические тесты, выявляющие соответствие ГСПЧ двум основным требованиям: равномерности распределения и независимости генерируемых чисел.
Тестирование равномерности распределения
Равномерность распределения можно проверять с помощью частотного теста. Суть этого теста состоит в построении эмпирического распределения чисел ri и его сравнении с теоретическим, т.е. равномерным распределением.
Для этого интервал (0,1) возможных значений ri разбивается на k одинаковых подынтервалов, генерируется выборка r1,…, rn, для каждого подынтервала определяется количество nj (j=1,…,k) тех псевдослучайных чисел, которые попали в этот подынтервал, и вычисляются относительные частоты f j = (nj / n) попаданий. Для идеального генера-
тора при n → ∞ выполняются условия
f j →1/ k, j =1,...,k, |
(2.1) |
т.е. частота f j попадания в интервал сходится к вероятности 1/ k попа-
дания в него стандартного случайного числа z. Из формулы (2.1) следует, что при n → ∞
kf j →1, j =1,...,k, |
(2.2) |
т.е. для идеального ГСПЧ эмпирическая плотность вероятностей kf j на каждом подынтервале сходится к теоретической. Для реального ГСПЧ
вычисляют величины kf j для нескольких достаточно больших значений n и проверяют, приближаются ли они с ростом n к 1.
Косвенная проверка равномерности распределения
Косвенная проверка равномерности распределения может быть осуществлена путем оценивания математического ожидания (МО) и дисперсии псевдослучайных чисел r1,…, rn. При равномерном распределении на (0,1) математическое ожидание и дисперсия равны 1/2 и 1/12 соответственно. Оценки M (математическое ожидание) и D (дисперсия) для выборки r1,…, rn рассчитываются по известным статистическим формулам
M = (r1 +... + rn ) / n = S1/ n ; |
|
(2.3) |
||
D = (r2 |
+... + r2 ) / n − M 2 |
= S2/ n − M 2 |
, |
(2.4) |
1 |
n |
|
|
|
где суммы S1 и S2 накапливаются в процессе генерации выборки. Очевидно, если выборка r1,…, rn характеризуется равномерным распределением, то M и D с ростом n должны сходиться к 1/2 и 1/12 соответственно. Это условие является необходимым для равномерности распределения чисел r1,…, rn, но не достаточным. Поэтому его выполнение лишь косвенно подтверждает (но не доказывает) гипотезу о равномерности распределения.
Проверка статистической независимости
Проверка независимости чисел на выходе ГСПЧ обычно производится путем измерения корреляции между ri и ri+g , где g > 0 – неко-
торое смещение. В случае, если установлена равномерность распределения, оценка Rg коэффициента корреляции между ri и ri+g может
быть получена по формуле
Rg = |
M[ri ri+g ] −1/ 4 |
=12M[ri ri+g ] −3 |
, |
(2.5) |
|
1/12 |
|||||
|
|
|
|
где M[ri ri+g ] – оценка математического ожидания произведения чисел
ri и ri+g (т.е. среднее значение произведений пар чисел, отстоящих в выборке на g шагов друг от друга),
M[r r |
] = |
1 |
(r r |
+... + r r |
) = |
Sg |
, |
(2.6) |
|
n − g |
n − g |
||||||||
i i+g |
|
1 1+g |
n n+g |
|
|
|
где сумму Sg можно накапливать в процессе генерации выборки. В случае независимости псевдослучайных чисел для любого g =1,2,..., n
должно выполняться условие Rg → 0 при n → ∞, которое означает по-
парную некоррелированность чисел. Следует обратить внимание на то, что некоррелированность является необходимым, но не достаточным условием независимости случайных величин.
Проверка длины периода
Поскольку последовательность чисел на выходе мультипликативного конгруэнтного ГСПЧ периодическая, она не может характеризоваться равномерным распределением и независимостью чисел в строгом смысле, но при большой длине l периода этот недостаток не приводит к ошибкам более существенным, чем, скажем, ограниченная длина разрядной сетки ЭВМ.
Выявление периода в последовательности r1,…, rn или, что то же самое, в последовательности x1,…, xn и определение его длины l – непростая задача, поскольку некоторое число первых членов последовательности может и не принадлежать его периодической части.
Определенную информацию о периодичности можно получить, если запомнить x1 и в процессе генерации выборки последовательно
сравнивать с ним числа xi, i=2,3,…,n. При первом совпадении xi = x1
определяется длина периода l=i–1. Если для i ≤ n, совпадения не произошло, то либо l ≥ n, либо периодическая часть последовательности начинается при i > 1.
Задание
1.Изучите способы анализа равномерности распределения и независимости чисел на выходе ГСПЧ.
2.Дополните программу из лабораторной работы №1 следующим функционалом:
– тестирование равномерности распределения ГСПЧ частотным методом разбиения на 10 интервалов (построить два графика
fi (n) для n=100 и n=10000, где fi – частота встречаемости случайной величины на i-м интервале);
–проверка равномерности распределения нахождением математического ожидания и дисперсии по формулам (2.3) и (2.4) для n=100 и n=10000;
–проверка (дополнительно, по усмотрению студента) стати-
стической независимости по формуле (2.5). Постройте график Rg(n) для n от 10 до 1000.
3. По рассчитанным оценкам сделайте вывод о пригодности ГСПЧ. Если ГСПЧ не пригоден, подберите для него более подходящие параметры a, m.
Содержание отчета
1.Цель работы.
2.Формулы для расчета статистических оценок, применяемых для анализа качества ГСПЧ.
3.Результаты расчета оценок (скриншоты), показывающие в графическом виде зависимость этих оценок от длины n выборки.
4.Вывод о пригодности ГСПЧ для его использования в статистическом моделировании.
5.Листинг программы.
Порядок выполнения работы
Для выполнения данной работы следует обратиться к программе, написанной в лабораторной работе № 1, и добавить в программу функции, соответствующие данной работе.
1.Открыть проект с программой в C++ Builder 6 (лабораторная работа № 1).
2.Добавить на форму объект PageControl с вкладки Win32 (рис. 2.1).
Рис. 2.1. Вкладка с объектами
3.Нажать правой кнопкой мыши на данном объекте и выбрать пункт NewPage (для создания двух вкладок – 2 клика).
4.Растянуть данный объект по размеру формы приложения, оставив свободное место для него перемещением имеющихся объектов в любое свободное пространство на форме (рис. 2.2).
Рис. 2.2. Объект PageControl
5.Переместить все существующие объекты на объект PageControl
сиспользованием выделения и копирования их в буфер обмена сочетанием клавиш ctrl+x и вставкой в PageControl с помощью ctrl+c.
6.Переименовать вкладки TabSheet1 и TabSheet2 в «Генерация чисел» и «Проверка генератора» соответственно (для этого кликнуть по объекту PageControl и слева в object tree view выбрать TabSheet1, переименовать его в параметре Caption окна Object Inspector на «Генерация чисел») (рис. 2.3).
7.Последующие работы будут добавляться наращиванием функционала данной программы добавлением новых вкладок.
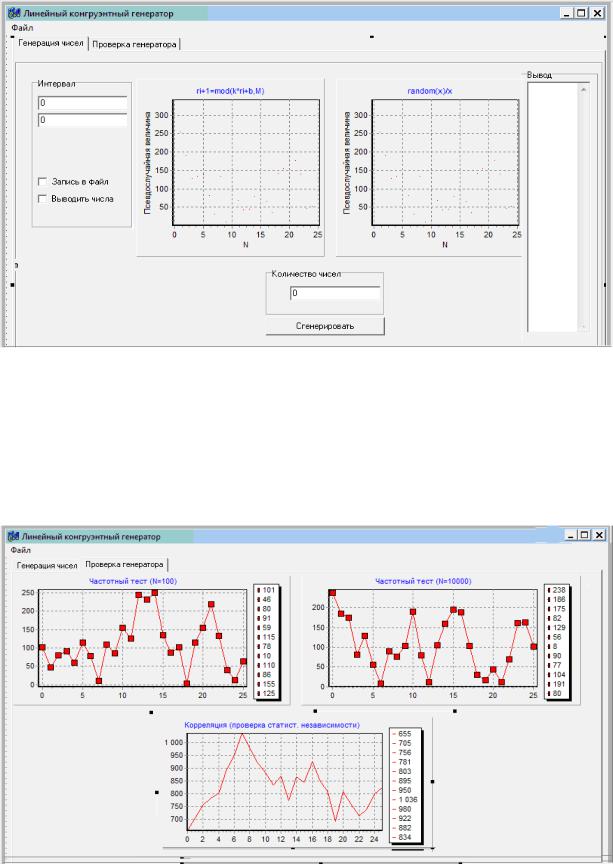
Рис. 2.3. Установка необходимых объектов
8. Перейти на вкладку «Проверка генератора» и установить 3 новых объекта Chart с добавлением в каждый из них по одному графику Series. Дать название каждому из графиков, как указано на рис. 2.4 (двойной клик на объекте Chart, на вкладке Titles).
Рис. 2.4. Создание графиков
9.Графики будут соответствовать следующим результатам: первые 2 графика для проверки частотным методом, один график – зависимость частоты встречаемости случайной величины на каждом из интервалов разбиения от номера интервала для N=100, другой – для N=10000. Третий график будет соответствовать зависимости коэффициента корреляции Rg от N (N следует брать от 10 до 10000).
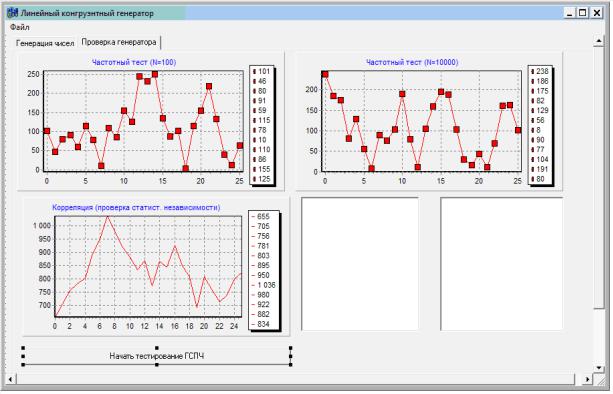
10.Добавить на форму кнопку Button, в поле caption дать ей название («Начать тестирование ГСПЧ»). Добавить 2 компонента Memo (рис. 2.5).
Рис. 2.5. Вывод текста
11.Вам необходимо нажать на кнопку «Начать тестирование ГСПЧ», назначить необходимые действия для заполнения всех трех графиков.
12.Первое, что должна выполнить программа, – сгенерировать первые 100 псевдослучайных чисел. Код можно скопировать с кнопки, генерирующей числа из первой лабораторной работы в кнопку «Начать тестирование ГСПЧ», но с изменением одного параметра – генерации фиксированного количества чисел, равного 100.
13.Код необходимо модифицировать так, чтобы сгенерированные числа записывались в массив. Инициализация массива на 100 чисел в С++ выглядит следующим образом:
float A[100].
14.По нажатию кнопки заполнение массива псевдослучайными числами можно реализовать следующим образом:
…
for (int i=0; i<100; i++)
{
//Здесь вы генерируете случайное число Х с помощью кода из лабораторной работы № 1// A[i]= X; // присваиваем i-му элементу массива значение Х
}
….
15. Проверить, правильно ли заполнился массив A[i] выводом его содержимого в компонент Memo:
for (int i=0; i<100; i++)
Memo2–>Lines->Add(A[i]);
16. Следующий этап – подсчет количества случайных величин в интервалах равной длины, составляющих всю сгенерированную последовательность. Разобьем последовательность на 10 интервалов: 0- 0,1; 0,1-0,2; 0,2-0,3; 0,3-0,4; 0,4-0,5; 0,5-0,6; 0,6-0,7; 0,7-0,8; 0,8-0,9; 0,9-
1,0. Реализация подсчета числа попавших чисел в интервалы может быть получена путем нахождения целого числа от умножения элемента A[i] (случайная величина) на 10 и прибавлением единицы. Например, если случайное число 0,25 умножить на 10 и отбросить дробную часть, то мы получим число 2, добавив единицу, и номер интервала, равный 3 (действительно, 0,25 находится в интервале 0,2-0,3) (рис. 2.6). Для проверки правильности подсчета установить еще один компонент Memo и выводить в него значения номеров интервалов. Проинициализировав новый массив B[10], содержащий информацию о каждом из интервалов, можно реализовать подсчет случайных чисел в каждом из интервалов следующим образом (выделение целой части можно сделать указанием (int) перед выводом числа):
for (int i=0;i<100;i++)
{
Memo2–>Lines–>Add(A[i]); //выводим случайную величину

buff=A[i]*10+1; // определяем номер интервала, которому она принадлежит
Memo3–>Lines–>Add((int)buff); //выводим номер этого интерва-
ла
B[(int)buff]+=1; //добавляем к счетчику единицу
}
Случайная величина |
Номер интервала |
Рис. 2.6. Вывод значений случайной величины
17. В массиве B[i] теперь подсчитано количество попавших чисел для каждого из интервалов. Выведем на первый график значения из массива B:
for (int i=0;i<10;i++)
Series4->AddXY(i,B[i]/100); // отношение попавших в интервал значений к общему их числу(определение fi).
18.Сделать копию блока кода для N=100 и поместить его следующим за текущим.
19.В скопированном блоке внести изменения, которые позволят генерировать 10000 значений и подсчитать их число в каждом из десяти интервалов (заменить в циклах 100 на 10000).
20.Отобразить на втором графике частоты встречаемости случайных величин на каждом из 10 интервалов (рис. 2.7).
21.Как видим, при переходе к N=10000 частотная составляющая приближается к вероятности попадания на каждый из интервалов, а именно 1/k=0,1.

Рис. 2.7. Интервалы
22. Поместить на форму 4 компонента Edit для вывода значений математического ожидания и дисперсии для N=100 и N=10000
(рис. 2.8).
Рис. 2.8. Вывод значений математического ожидания и дисперсии
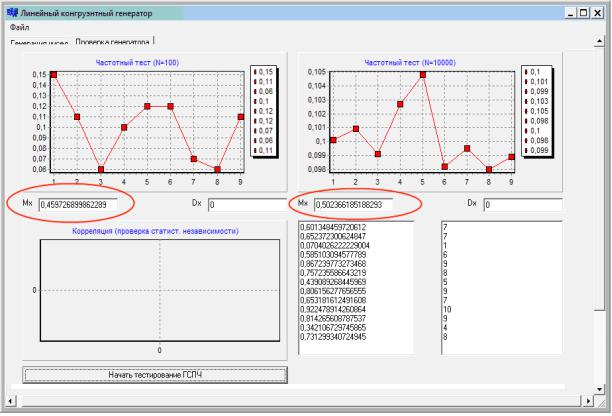
23. Найти значения математического ожидания для N=100 и N=10000 по формуле (2.3). Выводить полученные значения необходимо следующим образом:
Edit–9–>Text=Mx; // Mx – найденное математическое ожидание для 100 чисел, Edit может быть у вас под другим номером Edit10–>Text=Mx;// найденное математическое ожидание для 10000 чисел, Edit может быть у вас под другим номером.
Рис. 2.9. Вывод значений математического ожидания
24.Сгенерировать несколько выборок и следить за получаемыми значениями Mx. Для N=10000 они должны быть ближе к 0,5, чем при
N=100 (рис. 2.9).
25.В остальные 2 поля выводить значения дисперсии для N=100
иN=10000 по формуле (2.4).
26. Значение дисперсии с ростом N должно стремиться к 0,83333333 (1/12) и быть ближе к нему у выборки с N=10000
(рис. 2.10).
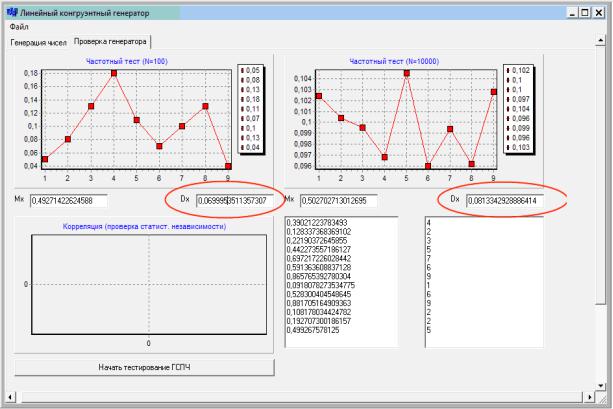
Рис. 2.10. Вывод значений дисперсии
27.Рассчитать (дополнительно, по усмотрению студента) значе-
ние Rg корреляции между парами чисел из выборки (g взять равным единице) при N от 10 до 1000 [сгенерировать 10 чисел, рассчитать Rg по формуле (2.5), вывести это значение на график, потом сгенериро-
вать 11 чисел, рассчитать Rg и вывести на график, потом 12, 13 чисел и т.д. до 1000]. Полученная кривая должна отражать приближение коэффициента корреляции Rg к нулю с ростом N (рис. 2.11).
28.Подписать оси на вкладке Axis каждого из графиков, как указано на рис. 2.11.
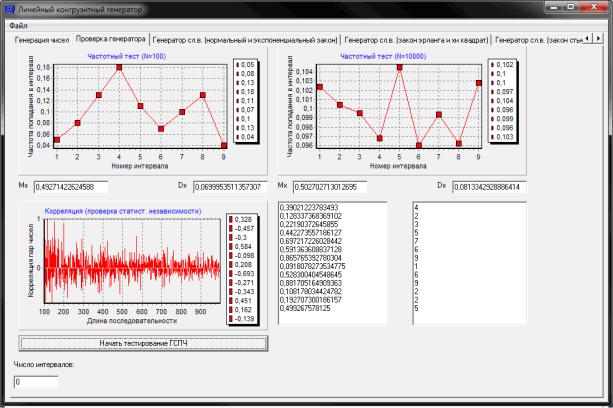
Рис. 2.11. Коэффициент корреляции. Итоговый результат
Контрольные вопросы
1.Как по выборке случайной величины рассчитываются оценки
еематематического ожидания и дисперсии?
2.Как проверяется равномерность распределения чисел с помощью частотного теста?
3.Как проверяется статистическая независимость чисел на выходе ГСПЧ?
Лабораторная работа №3
СИНТЕЗ ГЕНЕРАТОРОВ СЛУЧАЙНЫХ ВЕЛИЧИН С ЗАДАННЫМИ ЗАКОНАМИ РАСПРЕДЕЛЕНИЯ
Цель работы: разработать программный генератор псевдослучайных величин, имеющих заданный закон распределения.
Краткие сведения из теории
Общая схема реализации случайных величин
Случайная величина (СВ) с заданным законом распределения вероятностей всегда может быть получена путем подходящего преобразования стандартного случайного числа. При моделировании на ЭВМ такое подходящее преобразование выполняется над стандартным псевдослучайным числом, в результате получается псевдослучайная величина с требуемым распределением.
Метод обращения
Методом обращения можно получить СВ x с любой функцией распределения вероятностей (ФР) F(t), имеющей обратную функцию F -1. Метод обращения сводится к тому, чтобы сгенерировать стандартное случайное число z и вычислить x по формуле
x = F -1(z). |
(3.1) |
Тогда СВ х будет иметь распределение F(t). Если на «вход» формулы (3.1) подавать последовательность z1, z2,… стандартных случайных чисел, то на «выходе» получится последовательность x1, x2,… независимых СВ, имеющих ФР F(t). Для конкретной ФРВ F выражение обратной функции F -1(z) можно получить известным из школьного курса математики способом, состоящим в разрешении уравнения F(x) = z относительно x.
Докажем метод обращения. Пусть F – некоторая ФР. Тогда F – монотонно неубывающая функция, принимающая значения в интервале [0;1]. Пусть она имеет обратную функцию F -1. Определим х через
стандартную СВ z в виде x= F -1(z) и найдем ФР Fx(t) СВ х. По определению, Fx(t) = P[x≤t] (P–вероятность). Но P[x≤t] = P [F -1(z) ≤ t] =
=P[z≤F(t)]=F(t)]. Таким образом, Fx(t)=F(t), что и требовалось доказать.
Вкачестве примера рассмотрим использование метода обращения для реализации экспоненциальной СВ.
Реализация экспоненциальной случайной величины методом обращения
ФР экспоненциальной СВ уexp имеет вид
|
−ut |
,t ≥ 0; |
|
F(t) = 1−e |
|
(3.2) |
|
0, t < 0. |
|
||
Отсюда M[yexp ] =1/ u; D[yexp ] =1/ u2 .
В соответствии с методом обращения запишем уравнение z = F( yexp ) , или с учетом формулы (3.2)
z =1− euyexp (t ≥ 0) .
Решая его относительно yexp, найдем формулу для генерации СВ
yexp:
yexp = − |
1 ln(1− z) . |
(3.3) |
|
u |
|
В формуле (3.3) разность 1–z, как и сама величина z, является стандартным случайным числом. Этот факт позволяет упростить формулу для генерации yexp, полагая
yexp = − |
1 ln(z) . |
(3.4) |
|
u |
|
Назовем экспоненциальную СВ с МО, равным единице, норми-
рованной и обозначим через xexp. Тогда для xexp u=1 и для генерации xexp можно использовать формулу
xexp = −ln(z) . |
(3.5) |
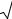
Применение линейных преобразований
Под линейным преобразованием (ЛП) СВ х будем понимать СВ y, полученную из х умножением на константу A и добавлением константы B:
y = Ax + B .
Очевидно,
M[ y] = M[Ax + B] = AM[x] + B ; |
|
D[y] = D[Ax + B] = A2 D[x]. |
(3.6) |
При построении генераторов СВ часто используется свойство ЛП y сохранять вид закона распределения СВ х. Так, например, если экспоненциальную СВ умножить на константу, то получится снова экспоненциальная СВ. Нормальная или равномерно распределенная сл.в. не меняет вида закона распределения как при умножении на константу, так и при добавлении константы.
Генератор нормированной экспоненциальной СВ xexp достаточен для реализации экспоненциальных СВ с любыми МО M ≥ 0 . Для получения экспоненциальной СВ xexp с МО M достаточно вычислить ее в
виде xexpM = M * xexp .
СВ y = Az + B , являющаяся ЛП стандартной СВ z, имеет равномерное распределение на интервале (B,A+B) и в соответствии с форму-
лой (3.6) M[y] = A / 2 + B ; D[y] = A2 /12 .
Реализация нормальной случайной величины методом суммирования
Плотность распределения вероятностей нормальной СВ х с МО M и дисперсией D =σ 2 имеет вид
|
|
1 |
|
e− |
(t−M )2 |
|
|
f (t) = |
|
|
2D . |
(3.7) |
|||
|
|
|
|||||
2πD |
|||||||
|
|
|
|
|
|
t
Соответствующая ФР F(t) = ∫ f (s)ds не выражается в элемен-
−∞
тарных функциях, что затрудняет непосредственное использование ме-

тода обращения. Поэтому для реализации нормальной СВ часто применяют метод суммирования, основанный на центральной предельной теореме теории вероятностей. Из этой теоремы вытекает, что сумма Sn достаточно большого числа n стандартных случайных чисел zi будет иметь распределение, достаточно близкое к нормальному.
Поскольку МО суммы Sn и ее дисперсия равны сумме МО и сумме дисперсий ее слагаемых, то M[Sn ] = n / 2; D[Sn ] = n /12 . Применим к
Sn линейное преобразование, чтобы получить нормированную центрированную СВ Х (с МО 0 и дисперсией 1). Очевидно, для этого надо по-
ложить |
x = |
(Sn − n / 2) |
или, заменяя Sn, |
|
||||||
|
|
|
|
|||||||
|
n /12 |
|
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
x = |
(z1 +... |
+ zn ) |
−n / 2 |
. |
(3.8) |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n /12 |
|
||
На практике часто принимают n=12, т.к., во-первых, при таком числе слагаемых Х имеет распределение, весьма близкое к нормальному, и, во-вторых, значительно упрощается вид формулы (3.8). При n=12 из формулы (3.8) получаем формулу для генерации нормированной центрированной СВ
xn0 = (z1 +... + z12 ) −6. |
(3.9) |
Нормальную СВ с МО M и дисперсией σ2 можно получить из xn0 по формуле
xnо = 
 Dxn0 + M .
Dxn0 + M .
В отличие от метода обращения метод суммирования является приближенным.
Применение функциональных преобразований случайных величин
Часто для реализации СВ, имеющих сложные законы распределения, можно применять функциональные преобразования СВ с простыми распределениями. Это связано с тем, что многие СВ, широко применяемые в теории вероятностей и математической статистике, вводятся именно как функции других СВ, которые имеют известные простые законы распределения.

Так, например, СВ, имеющая распределение Эрланга k-го порядка, вводится как сумма k независимых экспоненциальных СВ xexpi , которые имеют одинаковые МО:
xerl = (xexp1 +... + xexp k ). |
(3.10) |
Эту формулу можно непосредственно использовать для генерации xerl при наличии генератора для xexp. Если в формуле (3.10) сумми-
руются нормированные СВ xexp то, очевидно, что M[xerl ] = k * M[xexp ] =
= k /u и D[xerl ] = k * D[xexp ] = k / u2 .
Аналогично СВ χ2 (хи-квадрат), имеющая распределение с k степенями свободы, вводится как сумма k независимых СВ xnoi, имеющих нормированное центрированное нормальное распределение:
χ2 = xno12 +... + xnok |
2 ; M[χ2 ] = k; D[χ2 ] = 2k . |
(3.11) |
Из формулы (3.11) ясно, как она может быть реализована при моделировании на ЭВМ.
Распределением Стьюдента с k степенями свободы называют распределение СВ
xstu = |
xno0 |
, |
(3.12) |
|
|
|
 (x2no1 +... + x2nok ) / k
(x2no1 +... + x2nok ) / k
где xno0 ,..., xnok – независимые нормированные центрированные нормальные величины.
Генераторы дискретных случайных величин
Если x – дискретная СВ (ДСВ), то ее закон распределения вероятностей задается обычно путем указания вероятностей p1, p2, … для каждого ее возможного значения x1, x2,… соответственно.
Для реализации дискретной СВ интервал (0,1) разбивают на подынтервалы δ1,δ2 ,..., имеющие длину δ 1 = p1; δ 2 = p2 ,.... Такое раз-
биение всегда возможно, поскольку для дискретной СВ p1+p2+…=1. Далее СВ х может быть сгенерирована по следующему алгоритму:
1) генерируется стандартная СВ z;
2) определяется номер i подынтервала δi, в который попало значение z;
3) принимается x=xi.
В зависимости от значения z СВ х будет принимать различные значения из множества x1, x2 ,..., xi . При этом вероятность P[xi] принять некоторое значение xi равна, очевидно, вероятности того, что z попадет в подынтервал δi, т.е. P[xi ] = δi / (0,1) . Следовательно, P[xi ] = Pi для
всех i=1,2,3,… Это доказывает, что реализуется СВ х с требуемым распределением вероятностей.
При моделировании на ЭВМ вместо стандартной СВ z используется псевдослучайное число r. Строится сетка из значений вероятностей в зависимости от подынтервала i, точки которой рассчитываются по формуле
P |
= |
M i |
e−M , i = 0,1,2,... |
(3.13) |
|
||||
i |
|
i! |
|
|
|
|
|
||
Затем генерируется псевдослучайное число r и определяется, в какой интервал оно попало. Очевидно, формула Пуассона подразумевает различные длины интервалов и в какие-то из них псевдослучайная величина будет попадать чаще, что и позволит построить плотность распределения Пуассона.
Для того чтобы запрограммировать генерацию чисел по любому закону распределения ДСВ (в данном случае пуассоновскому), необходимо:
1. Сгенерировать псевдослучайное число Xi (код можно взять из лабораторных работ № 1 и 2).
2. После генерации числа вписать цикл while с условием «пока сгенерированное число Xi больше Pi».
3. В цикле while рассчитать значение Pi по формуле (3.13), с каждым последующим i значение Pi будет расти до тех пор, пока не дос-
тигнет Xi.
4. Выйти из цикла, когда значение Pi превысит сгенерированное число Xi.
5.После выхода из цикла while зафиксировать последнее значение
i(для Pi) и отразить на графике это значение i по горизонтальной оси и соответствующее ему значение Xi.
6.Повторить пункты 1–5 10000 раз.
Аналогично реализуются генераторы других дискретных псевдослучайных величин, например, СВ xber распределенная по закону Бернулли, имеет значение вероятности
Pi = Cni pi (1− p)n−i , i = 0,1,..., n ,
для нее M[xber ] = np; D[xber ] = np( p −1) , либо геометрическое распре-
деление Pi = Pi (1− p),i = 0,1,..., n .
В данном случае
M[xgeom ] = p /(1 − p); D[xgeom ] = p /(1 − p)2 .
Задание
1. Изучите методы синтеза генераторов СВ с заданными законами распределения.
2. Напишите программу, реализующую генератор псевдослучайной величины, закон распределения которой указан в табл. 3.1 (для вашего номера варианта), а также генератор чисел, распределенных по закону Пуассона.
Обеспечьте в программе:
–генерацию n значений псевдослучайной величины (рекоменду-
ется n = 10000);
–определение и вывод частот встречаемости случайной величины (плотность распределения) на каждом из интервалов и их последующее сравнение со значениями закона Пуассона и заданного закона
распределения (как в табл. 3.2 и 3.3 – экспоненциальный закон, где pi – теоретическая вероятность; pi* – статистическая вероятность).
По результатам сравнения с табличными значениями сделайте вывод о соответствии характера распределения случайных величин требуемому закону распределения. Разница между сгенерированными значениями и табличными не должна превышать 0,1.

Таблица 3.1
|
|
|
|
Название рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры рас- |
|
||||||
Вариант |
пределения ве- |
|
|
|
Закон распределения |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
пределения |
|
||||||||||||||||||||||||||||||||
|
|
|
|
роятностей |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M – любое (удоб- |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(t−M )2 |
|
|
|
нее брать M > 3, |
|
|||||||
|
1 |
|
Нормальное |
|
|
|
|
f (t) |
= |
|
|
1 |
|
|
|
e |
− |
|
|
|
чтобы избежать |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2D |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
работы с отрица- |
|
||||||||||||||||
|
|
|
|
|
|
2πD |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельными числа- |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ми), D = 1 |
|
||
|
|
|
Хи-квадрат с k |
|
|
|
f (t) = |
|
|
|
|
|
|
|
1 |
|
|
|
|
t k / 2−1e−t / 2 |
|
|
|
k = 4 |
|
|
|||||||||||||
|
2 |
|
степенями сво- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
2 |
k / 2 |
r(k / |
2) |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
боды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Стьюдента с k |
|
|
f (t) = |
r((k +1) / 2) |
(1 |
+t |
2 |
/ k) |
−(k+1) / 2 |
|
|
k = 4 |
|
|
||||||||||||||||||||||
|
3 |
|
степенями сво- |
|
|
|
|
|
|
|
r(k / 2) |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
nk |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
боды |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
4 |
|
Экспоненци- |
|
|
|
|
|
f (t) = ue−ut ,t ≥ 0 |
|
|
|
|
u = 1 |
|
|
|||||||||||||||||||||||
|
|
|
альное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
|
Эрланга k-го |
|
|
|
f (t) = |
|
|
uk |
k−1 |
|
|
−ut |
|
|
|
|
|
k = 3 |
|
|
|||||||||||||||||
|
|
порядка |
|
|
|
|
|
|
|
t |
|
|
|
e |
|
|
|
,t ≥ 0 |
|
|
|
u = 1 |
|
|
|||||||||||||||
|
|
|
|
|
(k −1)! |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Для всех |
Пуассона |
|
|
|
P = |
M i |
|
e−M , i = 0,1,2,... |
|
|
|
M = 4 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
i! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.2 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
pi |
|
0,0183 |
|
0,0733 |
|
0,1465 |
|
0,1954 |
|
0,1954 |
|
|
|
|
0,1563 |
|
|
0,1042 |
|
|
|
|
0,0595 |
|
0,0298 |
|
0,0132 |
|
0,0053 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
pi* |
|
0,0180 |
|
0,0750 |
|
0,1420 |
|
0,1960 |
|
0,1970 |
|
|
|
|
0,1520 |
|
|
0,1060 |
|
|
|
|
0,0610 |
|
0,0330 |
|
0,0120 |
|
– |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–
pi
–
pi*
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.3 |
||
0,6321 |
|
0,0855 |
|
0,0315 |
|
0,0116 |
|
0,0043 |
|
0,0016 |
|
0,0006 |
|
0,0002 |
|
0,0001 |
|
0,2325 |
|
|
|
|
|
|
|
|
|||||||||
0,6340 |
0,2280 |
0,0880 |
|
0,0310 |
|
0,0100 |
|
0,0050 |
|
0,0020 |
|
0,0000 |
|
0,0000 |
|
0,0000 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Содержание отчета
1.Цель работы.
2.Задание (указать вариант, формулы закона распределения моделируемой случайной величины из табл. 3.1).
3.Привести таблицу частот встречаемости СВ на каждом из интервалов вашего генератора, сравнить с данными в табл. 3.4–3.5 (при увеличении выборки N они должны сходиться к вероятностям, указан-
ным в таблицах).
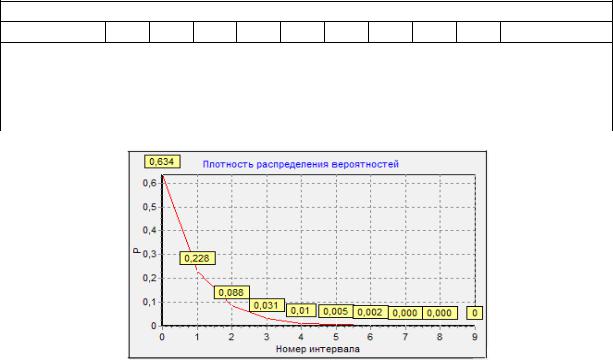
4. Привести результаты работы программы (скриншоты), на к о- торых будут изображены графики функции плотности распределения вероятностей (для двух законов распределения), как указано в примере (рис. 3.1, 3.2) (значения, подписанные у графика плотности распределения вероятностей, должны сходиться с табличными).
Обратить внимание на данные из табл. 3.5 для заданного закона распределения и сравнить табличные значения с полученными (например, табл. 3.3 – экспоненциальный закон распределения).
Обратить внимание на данные из табл. 3.4 для закона Пуассона и сравнить табличные значения с полученными (табл. 3.2).
5.Вывод о соответствии статистических характеристик реализованной псевдослучайной величины требуемым (разница не должна превышать 0,1).
6.Исходный код программы.
Таблица 3.4
Вероятности значений 0,…,10 дискретных случайных величин
0 1 2 3 4 5 6 7 8 9 10
Распределение Пуассона, m=4
0,0183 |
0,0733 |
0,1465 |
0,1954 |
0,1954 |
0,1563 |
0,1042 |
0,0595 |
0,0298 |
0,0132 |
0,0053 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.1. Плотность распределения вероятностей (экспоненциальный закон)
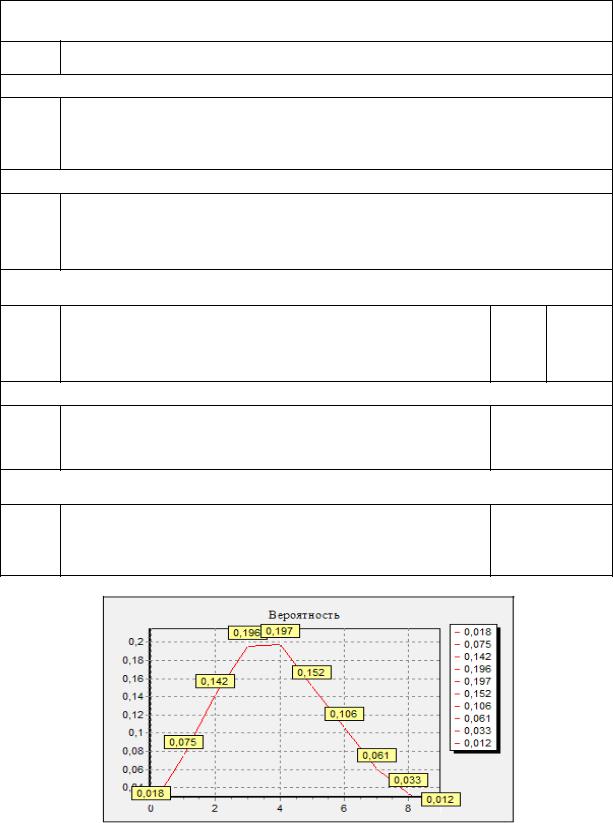
Таблица 3.5
(-1,0]
0,3413
Вероятности попадания непрерывных случайных величин
в интервалы от (-1,0] до (9,10]
(0,1] |
(1,2] |
(2,3] |
(3,4] |
(4,5] |
(5,6] |
|
(6,7] |
|
(7,8] |
|
(8,9] |
|
(9,10] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Нормальное распределение, M=1, D=1 |
|
|
|
|
|
|||||||
0,3413 |
|
|
|
|
|
– |
|
– |
|
– |
|
– |
|
– |
0,1359 |
0,0214 |
0,0013 |
0,00003 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Хи-квадрат
–
0,0902 |
0,1740 |
0,1780 |
0,1518 |
0,1187 |
0,0881 |
0,0633 |
0,0443 |
0,0305 |
0,0207 |
|
|
|
|
|
|
|
|
|
|
|
|
Стьюдента с 4-мя степенями свободы |
|
|
|
||||
0,3131
–
–
0,3131 |
0,1288 |
0,0381 |
|
0,0119 |
0,0044 |
0,0018 |
0,0008 |
0,0004 |
|
|
|
|
|
|
|
|
|
|
|
|
Экспоненциальное, u=1 |
|
||||
0,6321 |
|
|
|
|
|
|
|
|
0,2325 |
0,0855 |
|
0,0315 |
0,0116 |
0,0043 |
0,0016 |
0,0006 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Эрланга 3-го порядка, u=1 |
|
||||
0,0803 |
|
|
|
|
|
|
|
|
0,2430 |
0,2535 |
|
0,1851 |
0,1135 |
0,0627 |
0,0323 |
0,0159 |
|
|
|
|
|
|
|
|
|
|
––
0,0002 |
0,0001 |
|
|
0,0075 |
0,0035 |
|
|
Рис. 3.2. Закон распределения Пуассона
Контрольные вопросы
1.В чем заключается общий принцип реализации случайных (псевдослучайных) величин с заданными законами распределения вероятностей?
2.Как реализуется случайная величина по методу обращения?
3.Как при генерации СВ используют линейные преобразования?
4.Как можно реализовать нормальную СВ?
5.В каких случаях для реализации СВ со сложными законами распределения используются функциональные преобразования СВ, имеющие более простые распределения?
6.Каким образом можно построить генератор дискретной случайной величины?
