2. МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ

Метод начальных параметров – это способ решения дифференциальных уравнений, при котором неизвестными параметрами являются значения функции и ее производных в начале координат.

2.1.Построение полной математической модели изгиба

ирастяжения стержня при больших перемещениях при решении

задач методом начальных параметров

2.1.1. Геометрические соотношения

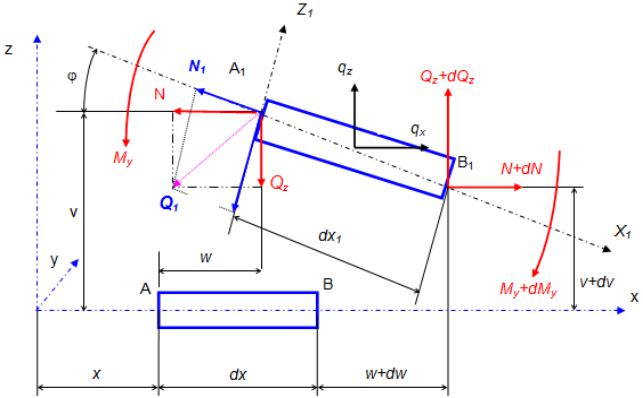
На рис. 2.1 изображено положение отрезка dx стержня с координатой x, отмеренной от левого конца стержня до нагружения, и положение того же отрезка длиной dz1 после нагружения распределенной по длине нагрузкой qx, qz,

Рис. 2.1. Положение элемента стержня до и после нагружения

где v, w – перемещения оси стержня по оси z и x соответственно; φ – угол поворота сечения относительно оси y.

Проектируя замкнутый контур АА1ВВ1А на оси x и z, получаем два геометрических соотношения

dv dx1 sin (v dv) 0 0,

20

2.1.2. Уравнения равновесия

Проектируя силы, действующие на отрезок dx1 на оси координат (см. рис.2.1), и рассматривая момент сил относительно точки В1, пренебрегая бесконечно малыми второго порядка малости, получаем три уравнения равновесия в неподвижной системе координат

N qx dx (N dN) 0,

откуда

dN qx dx.

Qz qz dx (Qz dQz ) 0,

откуда

dQz qz dx.

M y Qz dx1 cos N dx1 sin M y dM y 0,

откуда

dM y (Qz cos N sin ) dx1 .

2.1.3. Физические зависимости

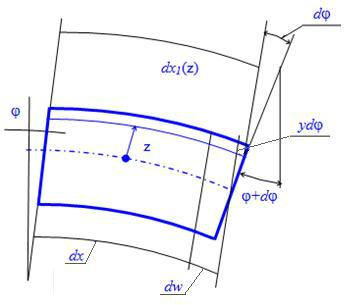
Рассмотрим подробно деформации и напряжения в выделенном элементе после нагружения.

Рис. 2.2. Изменение линейных размеров элемента стержня после нагружения

21

M y E J y ddx .

Следовательно,

d M y dx . EJ y

Учитывая полученные выражения для N1 и My, запишем формулу распределения нормальных напряжений в сечении стержня в виде

2.1.4. Полная математическая модель плоского изгиба и растяжения прямого стержня при больших перемещениях

Подставляя выражение (2.3) в (2.1), (2.2), после элементарных преобразований получаем систему дифференциальных уравнений для определения параметров v, w, , N, Qz, My

Система шестого порядка не линейна, содержит трансцендентные выражения и не имеет решений в элементарных функциях.

Шесть граничных условий для конкретной задачи всегда формулируются, так как при любом закреплении концов стержня на каждом известны три условия:

-жесткое закрепление v = 0, w = 0, = 0;

-шарнирно-неподвижное закрепление My = 0, v = 0, w = 0;

23

-шарнирно-подвижное закрепление My = 0, v = 0, N = 0;

-свободный конец My = 0, Qz = 0, N = 0 и т.д.

2.1.5. Математическая модель плоского изгиба и растяжения прямого стержня при малых прогибах

С 345, в пределах прочности, значения нормальных и касательных напряжений N/A, Qz/A не могут превышать 2 350 ‒ 3 450 кгс/см2, а модуль нормальной упругости (модуль Юнга) Е=2 100 000 кгс/см2. Таким образом, N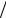(EА) и Qy 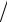(EА) < 0,01.

C учетом сказанного система дифференциальных уравнений (2.4) упрощается и принимает вид

24