где коэффициенты пропорциональности E и G называются соответственно модулями упругости первого (модуль Юнга) и второго рода.

1.5. Внутренние силы как интегральные характеристики напряжений

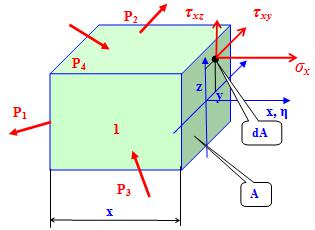
Определим внутренние силы путем интегрирования (суммирования) напряжений, действующих в точках плоскости сечения

(рис.1.10) [1,2]

Рис. 1.10. Внутренние силы как интегральные характеристики напряжений

На бесконечно малой площадке dA = dx · dy продольная сила dN = σz· dA. Если взять двойной интеграл по всей площади сечения, то получим полную продольную силу в сечении

N (x) z (x, y)dA. (1.15)

A

Аналогичным образом составим выражения остальных внутренних сил

Qy (x) xy ( y, z) dA;

A

Qz (x) xz ( y, z) dA;

A

M y (x) x ( y, z) z dA;

A

M z (x) x ( y, z) y dA;

A

M k (x) ( xz ( y, z) y xy ( y, z) z) dA.

A

13

1.6. Геометрические характеристики поперечных сечений

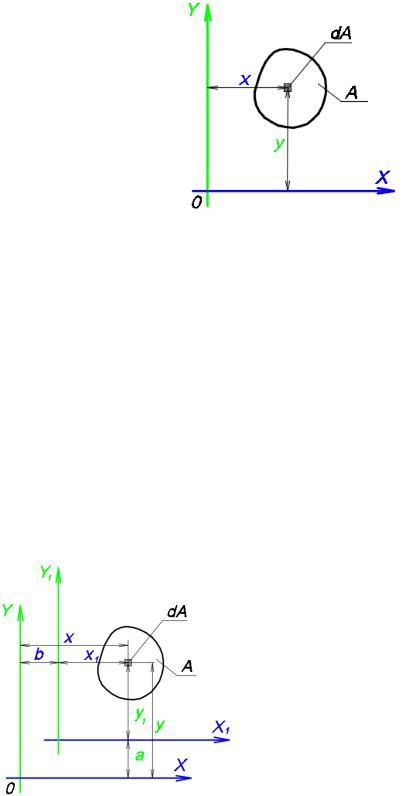
Статическими моментами площади сечений называются интегралы следующих видов (рис. 1.11) [3]

S x ydA;

A

S y xdA.

A

Размерность статических моментов м3, см3.

Статический момент площади сечения может быть больше нуля, меньше нуля и равным нулю. Ось, относительно которой статический момент равен нулю, называется центральной.

Следовательно, пересечение центральных осей дает центр тяжести сечения.

Исходя из свойств определенного интеграла, который можно вычислять по частям, получаем, что статический момент площади сложного сечения равен сумме статических моментов площадей его частей.

1.7. Определение положения центра тяжести

Рассмотрим изменение статического момента площади при параллельном переносе осей координат (рис.1.12),

Рис. 1.12. Определению статических моментов относительно параллельно перенесенных осей

14

где x, y – исходные оси координат, x1, y1 – перенесенные оси координат.

y1 = y – a; x1 = x – b.

По определению

Sx1 ( y a)dA ydA a dA Sx aA;

A A A

S y1 (x b)dA xdA b dA S y bA.

A A A

Таким образом, чтобы оси стали центральными, их нужно сместить на расстояние, равное

Sx1 Sx aA 0;

a yc SAx .

S y1 S y bA 0; b xc SAy .

1.8. Моменты инерции сечений

Моментами инерции сечений называются интегралы вида [3]:

– осевой момент инерции относительно оси x

I x y 2 dA;

A

– осевой момент инерции относительно оси y

I y x2 dA;

A

– центробежный момент инерции сечения

I xy xydA;

A

– полярный момент инерции сечения

I 2 dA;

A

Размерность статических моментов м4, см4

15

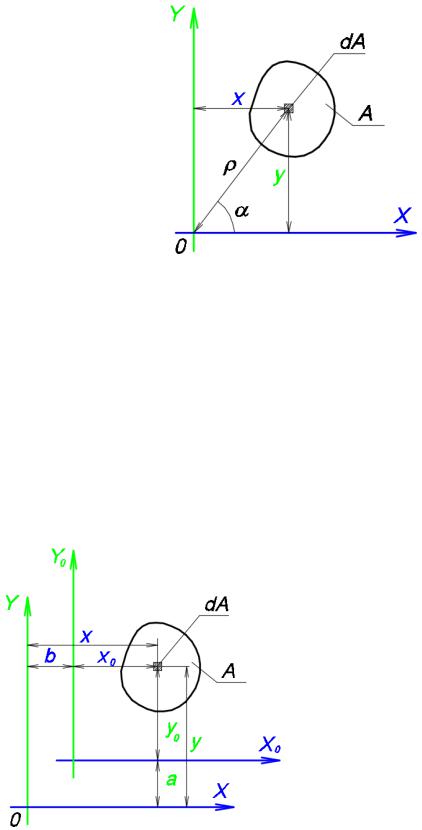
Осевые моменты инерции всегда положительные. Центробежный момент может быть как больше нуля, так и меньше нуля и равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения. Оси симметрии всегда являются главными. Полярный момент инерции равен сумме осевых моментов инерции (рис. 1.13).

Рис. 1.13. Связь полярных и декартовых координат элементарной площадки

1.9. Моменты инерции относительно параллельных осей

Рассмотрим изменение момента инерции при параллельном переносе осей координат (рис. 1.14),

Рис. 1.14. Момент инерции относительно параллельных осей

где x, y – исходные оси координат, x1, y1 – перенесенные оси координат.

16