нии x можно определить по известным внешним силам, приложенным к левой (первой) части стержня
n
Qx(x) = - ( Pix ),
i 1 n
Qy(x) = - ( Piy ),
i 1 n
Qz(x) = - ( Piz ),
i 1 n
Mx(x) = - ( M ix ),
i 1 n
My(x) = - ( M iy ),
i 1 n
Mz(x) = - ( M iz ),
i 1
где n – количество внешних сил, действующих на первую часть стержня (см. рис.1.4, а).
1.4. Понятие о напряжениях и деформациях. Закон Гука
Количественной характеристикой распределения внутренних сил по сечению нагруженного стержня является механическое напряжение [1,2]. Вблизи точки сечения А (y;z) выделим бесконечно малую площадку A, на которой действует вектор внутренних сил q (рис.1.5). Отношение
q рсрA
называется вектором среднего полного напряжения на площадке. Если устремить величину площадки к нулю, то получим вектор полного напряжения в точке А(y;z) сечения x
lim( A 0) q p .
F
Напряжение имеет размерность Н/м2 = Па. Один паскаль (1Па) является малой величиной, определяющей, с какой интенсивностью действует на плоскость сила, равная 1 Н, равномерно распределенная по площади 1 м2. Поэтому на практике используют понятие 1МПа = 1·106 Па. В инженерной практике используются кгс/м2, тс/м2.
9
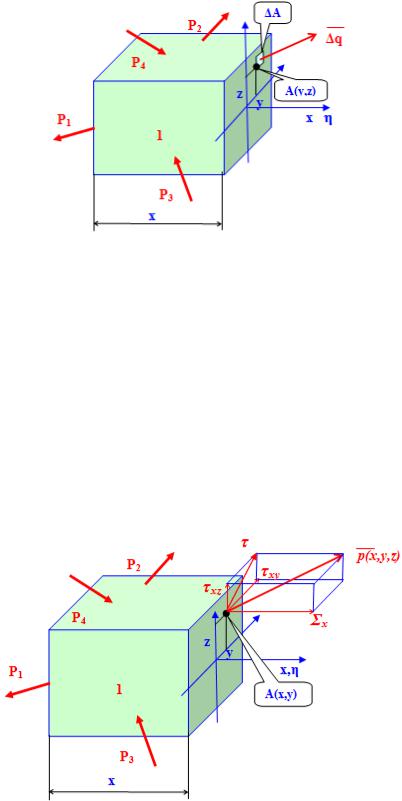
Рис. 1.5. Вектор внутренних сил на бесконечно малой площадке
Напряжением называется интенсивность действия внутренних сил в точке тела или внутреннее усилие, приходящееся на единицу площади [1,2].
Вектор полного напряжения p в проекциях на нормаль η и
плоскость сечения дает нормальное σ и полное касательное τ напряжения. В то же время полное касательное напряжение имеет две составляющие в проекциях на оси в плоскости сечения. Так, если сечение проведено перпендикулярно оси x, совпадающей в данном случае с нормалью сечения η, компонентами вектора полного напряжения будут нормальное напряжение σx и касательные напряжения τxy, τxz
(рис.1.6).
Рис.1.6. Проекции полного напряжения в точке сечения с нормалью, совпадающей с осью x
10
Если вблизи точки А вырезать бесконечно малый параллелепипед с гранями, нормали к которым совпадают с осями x, y, z, то можно увидеть полную картину напряжений (рис. 1.7).
Рис. 1.7. Обозначение и ориентация компонентов напряженного состояния
Итак, напряженное состояние в точке твердого деформируемого тела характеризуется девятью компонентами напряжений, которые принято записывать в виде тензора напряжений
|
|
|
x |
xy |
xz |
|
|
|
|
|
|
|
|||
|
T |
|
yx |
y |
yz |
. |
|
|
|
|
zx |
zy |
z |
|
|
Следуя |
закону |
парности |
касательных |
напряжений |
|||
( xy xz yz ), напряженное состояние в точке можно описать ше-
стью компонентами.
Понятие о деформациях рассмотрим на примере растяжения стержня длинной L постоянного квадратного сечения а·а (рис. 1.8).
При растяжении стержня изменяются его размеры, при этом величины L = L(P) – L , а = а(P) – а называются абсолютными изменениями размеров. Величины
L x ,
L
a y z a
11
называются относительными изменениями размеров или линейными деформациями. Существует линейная зависимость между продоль-
ными z и поперечными деформациями
y x = - x ,
где μ – коэффициент Пуассона (физическая постоянная материала). Так, для конструкционных сталей = 0,25 – 0,3.
Рис. 1.8. Деформации в стержне
Кроме изменения размеров тела при нагружении следует различать угловую деформацию, которая отражается изменением прямого угла, изображенного в какой-либо плоскости тела. На рис. 1.8 изображена угловая деформация (угол сдвига) в осях 1-2: 12 1 2 .
Угловая деформация приводит к изменению формы тела.
В пределах малых (упругих) деформаций существует линейная зависимость между напряжениями и деформациями (рис.1.9). Эта зависимость носит название закона Гука.
Рис. 1.9. Иллюстрация к закону Гука
Таким образом, в пределах упругих деформаций справедливы соотношения
σ = E·ε,
τ = G·γ,
12