
1944
.pdf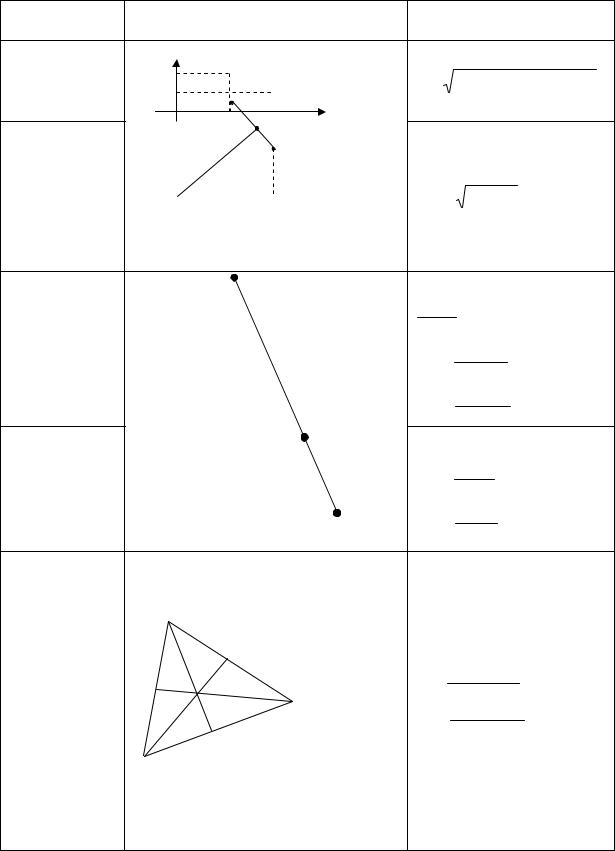
|
|
|
|
Метод координат |
|
|
|
|
|
|
|
||
Основные |
|
|
Поясняющий рисунок |
|
Расчетная формула |
|
|||||||
задачи |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Расстояние |
|
Y |
|
|
|
|
|
|
|
|
|
|
|
между |
|
|
M1 x1, y1 |
d x |
2 x1 |
2 |
y2 |
y1 |
2 |
||||
точками |
|
y1 |
|
|
|||||||||
|
|
|
y2 |
|
M (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
M 2 x2 , y2 |
|
|
|
|
|
|
|
||
Расстояние от |
|
|
|
|
|
|
|
|
|
||||
точки до |
|
|
|
|
|
dM |
x2 y2 |
|
|
|
|||
начала |
|
|
O |
x1 |
x2 |
X |
|
|
|
|
|
|
|
координат |
|
|
|
|
|
|
|
|
|
|
|
|
|
Координаты |
|
М1(x1, y1) |
|
|
M1M MM2 |
или |
|
|
|||||
|
|
|
|
|
M1M ; |
|
|
|
|
||||
точки, |
деля- |
|
|
|
|
|
|
|
|
||||
щей отрезок в |
|
|
|
|
MM2 |
|
|
|
|
|
|||
|
|
|
|
|
x1 |
x2 , |
|
|
|
||||
данном |
отно- |
|
|
|
|
xM |
|
|
|
||||
шении |
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
yM |
y1 y2 |
|
|
|
|
|
|
|
|
|
|
|
M(x, y) |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
M1M MM2 , 1, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Координаты |
|
|
|
|
|
x |
x1 |
x2 , |
|
|
|
|
|
середины |
|
|
|
|
|
M |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
отрезка |
|
|
|
M2(x2, y2) |
yM |
y1 y2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
M1(x1,y1,z1) |
|
|
|
|
|
|
|
|
|
|
Координаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
центра |
тяже- |
|
С |
|
|
|
x1 x2 x3 , |
|
|
||||
сти треуголь- |
|
|
|
xС |
|
|
|||||||
ника |
(С |
– |
|
|
|
M2(x2,y2,z2 ) |
yС |
y1 |
3 |
|
|
|
|
точка |
пересе- |
|
|
|
|
y2 y3 |
|
|
|||||
чения |
медиан |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
треугольника) |
M3(x3,y3,z3) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
26 |
|
|
|
|
|
|
|

Уравнения прямой на плоскости
Название
Вид уравнения Рисунок
уравнения
Общее |
Ax By C 0, |
n |
|
||
где n(A,B) − нормаль |
|
|
уравнение |
|
|
прямой |
к прямой, A2 B2 0 |
|
Уравнение |
x |
y |
|
||
прямой |
|
||||
«в отрезках» |
|
|
|
1 |
b |
|
|
||||
a |
b |
|
|||
a
Уравнение
прямой с угловым
y kx b, |
k tg |
|
коэффициентом |
|
|
|
|
k
Уравнения пучка прямых ,
проходящих y y0 k x x0 через точку
x0, y0
Уравнение |
|
|
|
|
прямой, |
x x1 |
|
y y1 |
|
проходящей |
|
|||
x2 x1 |
y2 y1 |
|||
через точки |
|
x1, y1 , x2, y2
Нормальное |
xcos ysin p 0 |
p |
уравнение |
||
прямой |
|
|
27

|
Взаимное расположение прямых |
|
|
|
||||
|
|
|
Условия расположения прямых по способу |
|||||
Расположение прямых |
|
задания |
|
|
|
|||
y k1x b1 |
A1x B1y C1 0 |
|||||||
|
|
|
||||||
Параллельность |
|
y k2x b2 |
A2x B2 y C2 0 |
|||||
|
|
|
A1 B1 ; |
|
||||
|
|
|
|
|
|
|||
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
k1 k2 |
если прямые |
||||
|
|
|
совпадают, то |
|||||
|
|
|
|
A1 B1 |
С1 |
|||
|
|
|
|
A2 |
B2 |
С2 |
||
Перпендикулярность |
|
|
|
|
|
|||
|
|
|
k1 k2 1 |
A1 A2 B1B2 0 |
||||
|
Пересечение |
|
|
|
|
|
|
|
|
|
|
|
tg A1B2 A2B1 |
||||
|
|
|
k2 k1 |
|
A1A2 B1B2 |
|||
|
|
|
|
|
|
|||
|
|
|
tg |
|
|
n1 n2 |
||
|
|
|
1 k1k2 |
|
|
|||
|
|
|
или соs |
|
||||
|
|
|
|
|
|
n1 n2 |
||
Нахождение общих точек |
y k1x b1; |
A1x B2y C1 |
0; |
|||||
|
прямых |
|
|
|
|
|
0 |
|
|
|
y k2x b2 |
A2x B2y C2 |
|||||
Расстояние от точки M0 x0, y0 до прямой Ax By C 0: |
||||||||
_______ |
|
M0 |
|
|
|
|
||
d прn M0M M |
d |
|
|
|
|
|||
|
d Ax0 By0 |
C |
||||||
|
|
|
|
|||||
|
|
|
|
|
A2 B2 |
|||
28

Кривые второго порядка
Определение |
|
|
|
|
Рисунок |
|
|
|
|
|
|
Уравнение |
|
|
|
|||||||||||||||||
кривой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Эллипс – гео- |
|
|
|
|
|
|
|
|
Каноническое уравнение: |
|
||||||||||||||||||||||
метрическое |
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
x2 |
y2 |
1, |
|
|
|
|||||||||||
место |
точек |
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
a |
2 |
|
b |
2 |
|
|
|
|
|
|
|
|||||
плоскости, |
для |
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
a – боль- |
|
||||||||||||
|
|
|
|
|
|
|
где а2 с2 |
b2; |
|
|||||||||||||||||||||||
каждой |
из |
ко- |
|
|
|
|
|
|
|
a |
шая полуось, b – малая |
|
||||||||||||||||||||
торых |
сумма |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
расстояний |
до |
|
|
F2 |
|
с F1 |
X |
полуось. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Уравнение эллипса со |
|
|||||||||||||||||||||||||||
двух |
фиксиро- |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
смещенным центром |
|
|||||||||||||||||||||||
ванных |
точек |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
С(x0, y0 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
(фокусов) |
F1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
F (c,0), |
F ( c,0) – |
|
|
|
x x |
0 |
2 |
|
|
y y |
0 |
2 |
|
|||||||||||||||||||
F |
есть вели- |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
фокусы; c – половина |
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
b2 |
|
|
|
|
||||||||||
чина |
|
постоян- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
расстояния между |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
c |
a2 |
b2 |
|
|
|
|
|
|
|
|||||||||||||||||||
ная |
|
(равная |
|
|
|
– |
|
|
|
|
|
|
||||||||||||||||||||
2a), |
|
большая |
фокусами; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
чем |
расстояние |
|
M − произвольная точка |
эксцентриситет эллипса, |
|
|||||||||||||||||||||||||||
между |
фоку- |
эллипса, тогда |
|
характеризующий степень |
|
|||||||||||||||||||||||||||
|
F M |
|
F M |
2a 2c; |
|
|||||||||||||||||||||||||||
сами |
|
|
|
|
сжатия кривой, 0 1 |
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
С(0,0) – центр эллипса |
|
|
Параметрические |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
|
|
|
|
эллипса |
с |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
центром С (0,0): |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x acost, |
0 t 2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y bsint, |
|
|
|
|
|
|
|
||||||||||
Окружность |
|
|
|
|
|
|
|
|
|
Каноническое уравнение: |
||||||||||||||||||||||
− частный |
|
|
Y |
|
|
|
|
x2 y2 R2 , С(0,0). |
|
|
|
|||||||||||||||||||||
случай эллипса |
|
|
|
|
|
|
|
|
|
Уравнение |
|
|
окружности |
|||||||||||||||||||
(a b) |
|
|
|
|
|
|
R |
|
|
|
|
|||||||||||||||||||||
|
|
y0 |
|
|
со |
|
смещенным |
|
|
|
|
центром |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
С(x0, y0 ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
|
2 |
y y |
0 |
2 |
R2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
O |
|
x0 |
X |
|
Уравнение окружности в |
||||||||||||||||||||||
|
|
|
|
|
|
полярных координатах: |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
С(x0 , y0 )– центр |
1) С(0,0) r R, |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2) С(R,0) r 2Rcos ; |
|
|||||||||||||||||||||||||
|
|
|
|
|
окружности, R – радиус |
3) С(0,R) r 2Rsin . |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
окружности |
|
Параметрические |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
уравнения |
|
окружности |
с |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
центром |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x Rcost, |
0 t 2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
С(0,0): |
|
|
|
|
Rsint, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||||||||
29

Окончание таблицы
Гипербола – |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Каноническое |
|
|
|
|
|
|
|
||||||||||||||||||||||||
геометричес- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение: |
|
|
x |
2 |
|
|
y |
2 |
1, |
|||||||||||||||||||||||
кое |
|
место |
то- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
M(x, y) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|||||||||||||||||||||||||
чек плоскости, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где с2 а2 |
|
|
b2; a – |
|||||||||||||||||||||||||||||
для каждой из |
|
F2 |
|
|
|
|
|
|
a |
F1 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
которых |
абсо- |
|
|
|
|
|
|
|
|
действительная полуось |
|||||||||||||||||||||||||||||||||||||||||||||
лютная |
вели- |
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
полуось, b – мнимая |
|||||||||||||||||||||||||||||||||||||
чина |
разности |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
полуось. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
расстояний |
до |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Каноническое уравне- |
||||||||||||||||||||||||||||||
двух |
фиксиро- |
|
F (c,0), F ( c,0) – фокусы; |
ние сопряженной гипер- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ванных |
точек |
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
болы (изображена на рис. |
||||||||||||||||||||||||||||||||||||
(фокусов) |
|
F , |
c – половина |
расстояния |
штриховой линией): |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
между |
|
|
фокусами; |
M − |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
F2 |
есть |
вели- |
|
|
|
|
|
|
|
|
y |
|
x |
|
|
|
1 |
||||||||||||||||||||||||||||||||||||||
произвольная точка |
эллипса, |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
2 |
||||||||||||||||||||||||||||||||||||||||||||||||
чина |
постоян- |
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Уравнение гиперболы с |
||||||||||||||||||||||||||||||||||||||||||||
ная |
|
(равная |
|
F1M |
|
|
|
F2M |
|
2a 2c |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
центром в точке С(x0 , y0 ): |
||||||||||||||||||||||||||||||||||||||||||||||||||
2a), меньшая, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
чем расстояние |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 2 |
|
|
y y0 2 |
1 |
|||||||||||||||||||||||||||
между фоку- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2 |
|
|
|
|
|
|
|
|
|
|
|
b2 |
|||||||||||||||||
сами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эксцентриситет |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
a2 b |
2 |
|
|
|
1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
a |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнения |
|
|
|
|
|
|
|
|
|
асимптот |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гиперболы: y |
b |
x |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||
Парабола |
– |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если F( |
p |
|
;0), то |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M(x, y) |
|
|
||||||||||||||||||||||||||||||||||
геометричес- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
кое |
|
место |
то- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
каноническое уравнение |
||||||||||||||||||||||||||||||||
чек плоскости, |
|
|
|
|
|
|
|
|
|
A |
|
|
|
O F |
|
|
|
параболы: |
y2 2px; |
||||||||||||||||||||||||||||||||||||
для каждой из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнение директрисы |
|||||||||||||||||||||||||||||||
которых |
рас- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
||||||||||||
стояние |
|
до |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параболы: x |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
точки (фокуса) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
2 |
|
|
|
|
|
|
|
|||||||||
F |
равно |
рас- |
|
AF |
|
p – параметр параболы, |
|
Если F(0; |
|
|
), то |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
стоянию |
|
до |
|
F( |
p |
;0) |
|
|
– фокус, тогда |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
некоторой |
|
|
|
|
каноническое уравнение |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
фиксирован- |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
параболы: |
x2 2py ; |
|||||||||||||||||||||||||||||||||||
|
MF |
|
|
|
MN |
|
, |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
ной |
|
прямой – |
|
|
|
|
|
|
|
|
уравнение директрисы |
||||||||||||||||||||||||||||||||||||||||||||
директрисы |
|
|
AN – директриса |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
параболы: |
x |
p |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
2
30

a |
В ПРОСТРАНСТВЕ |
|
|
прba b |
Системы координат в пространстве |
Уравнения связи Название системы и способ задания между
координатами
Декартова (прямоугольная) система координат (ДСК)
Z |
|
|
|
|
O − |
начало |
коор- |
|
|
|||
|
|
|
|
|
|
динат; |
|
|
|
|
|
|
|
|
|
M x,y,z |
OX |
− ось абсцисс; |
|
|
|||||
|
|
z |
OY |
− ось ординат; |
|
|
||||||
O |
|
|
y |
Y |
OZ |
|
− |
ось |
|
|
||
|
|
|
|
|
|
|||||||
x |
|
|
|
|
аппликат; |
|
|
|
|
|||
|
|
|
|
x,y,z − коор- |
|
|
||||||
|
|
|
|
|
|
|
|
|||||
X |
|
|
|
|
динаты точки M |
|
|
|||||
Цилиндрическая система координат |
|
|
|
|
||||||||
Z |
|
M r, ,z |
r − длина радиуса- |
|
|
|||||||
|
|
|
вектора |
проекции |
x rcos , |
|||||||
|
|
|
z |
|
точки |
|
M |
на |
||||
|
|
|
Y |
плоскость |
XOY ; |
|
|
|||||
O |
|
|
|
y rsin , |
||||||||
r |
|
|
|
− угол, образован- |
|
z z |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
ный |
|
радиус-век- |
r 0, 0 2 , z R |
|||
X |
|
|
|
|
тором |
M |
проекции |
|
|
|||
|
|
|
|
точки |
с |
осью |
|
|
||||
|
|
|
|
|
|
OX ; |
|
z |
− |
|
|
|
аппликата точки M ; r, ,z − координаты точки M |
|
|
||||||||||
Сферическая система координат |
|
|
|
|
||||||||
Z |
|
M r, , |
O − начало координат; |
|
|
|||||||
|
|
r |
r − длина радиуса- |
x rcos sin , |
||||||||
|
z |
|
вектора точки M ; − |
|||||||||
|
Y |
угол, |
образованный |
|
|
|||||||
O |
|
|
|
y rsin sin , |
||||||||
|
|
|
|
радиус-вектором |
|
z rcos |
||||||
|
|
|
|
|
проекции |
точки |
M с |
|
||||
X |
|
|
|
|
осью OX ; − |
угол |
r 0, 0 2 , 0 |
|||||
|
|
|
|
отклонения |
радиуса- |
|
|
|||||
|
|
|
|
|
|
вектора |
|
____ |
от оси |
|
|
|
|
|
|
|
|
|
|
OM |
|
|
|||
OZ ; r, , − координаты точки M |
|
|
|
|
|
|
||||||
25
Уравнения плоскости
Способ задания |
|
|
|
|
|
|
|
Вид уравнения |
|
|
|
||||||||||
Уравнение плоскости, про- |
A x x0 B y y0 C z z0 0 |
||||||||||||||||||||
ходящей |
через |
точку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M0 x0,y0,z0 , |
перпендику- |
|
|
|
|
|
|
|
|
|
|
N A,B,C |
|||||||||
лярно вектору N A,B,C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
M0 |
|
|
|
|
|
|
|
|
|
||||
Вектор |
N A,B,C |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
нормальный вектор плоскости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Общее уравнение плоскости |
|
Ax By Cz D 0, где |
|
|
|
||||||||||||||||
|
|
|
|
A2 B2 C2 |
0 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
x |
|
y |
|
z |
1, где a,b,c 0 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
a b |
c |
|
|
|
|
|
|
|
|
|
||||||
Уравнение плоскости |
|
|
|
|
|
Z |
c |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
«в отрезках» |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
Y |
|
|
|
||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x x1 |
|
y y1 |
|
z z1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
Уравнение плоскости, |
|
|
x2 x1 |
|
y2 y1 |
z2 z1 |
0 |
||||||||||||||
проходящей через три данные |
|
x3 x1 |
|
y3 y1 |
z3 z1 |
|
|
|
|||||||||||||
точки M1 x1, y1,z1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
M2 x2, y2,z2 , M3 x3, y3,z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
M1 |
M3 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
M2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
|
плоскости, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проходящей |
|
через |
точки |
|
x x1 |
|
y y1 |
|
z z1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||||||||
M1 x1, y1,z1 , |
M2 x2, y2,z2 , |
|
x2 x1 |
|
y2 y1 |
z2 z1 |
|
|
0 |
||||||||||||
параллельно |
|
вектору |
|
|
|
|
|||||||||||||||
а (ах ,ay ,az ) |
|
|
|
ax |
|
|
ay |
|
|
az |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26

Частные случаи положения плоскости в пространстве
Положение плоскости и |
Поясняющий рисунок |
|||
вид общего уравнения |
||||
|
||||
Плоскость параллельна |
Z |
|||
|
||||
координатной оси |
Y |
|||
OX : By Cz D 0( A 0) |
||||
OY : Ax Cz D 0(B 0) |
X |
|||
OZ: Ax By D 0(C 0) |
By Cz D 0 |
|||
|
|
|
||
|
|
|
|
|
|
|
|
Z |
|
Плоскость проходит через начало |
|
|||
координат |
Y |
|||
Ax By Cz 0(D 0) |
X |
|||
|
|
|
||
|
|
|
|
|
Плоскость параллельна |
Z |
|||
|
||||
координатным осям |
|
|||
OX и OY: Cz D 0 ( A B 0) |
Y |
|||
OX и OZ: By D 0 |
( A C 0) |
X |
||
OY и OZ: Ax D 0 |
(B C 0) |
|||
|
|
|
Cz D 0 |
|
|
|
|
Z |
|
Плоскость проходит через ось |
|
|||
OX: By Cz 0 ( A D 0) |
Y |
|||
OY: Ax Cz 0 |
(B D 0) |
|||
|
||||
OZ: Ax By 0 |
(C D 0) |
X |
||
|
|
|
By Cz 0 |
|
|
|
|
|
|
|
|
|
Z |
|
Уравнения координатных |
|
|||
плоскостей |
Y |
|||
XOY: z 0( A B D 0) |
||||
XOZ: y 0 ( A C D 0) |
X |
|||
|
|
|
||
YOZ: x 0 (B C D 0)
z 0
27

Взаимное расположение плоскостей |
|
|
||||||
|
Условия расположения плоскостей |
|||||||
Расположение плоскостей |
A1x B1y C1z D1 0 |
|
||||||
|
A2x B2y C2z D2 0 |
|||||||
Параллельность |
N1 (A1,B1,C1), N2 (A2,B2,C2) |
|||||||
N2 |
N || N |
|
A1 B1 C1 . |
|
||||
1 |
|
2 |
|
A2 |
B2 |
C2 |
|
|
N1 |
В частности, если плоскости |
|||||||
|
|
|
|
совпадают, то |
|
|||
|
|
|
A1 B1 C1 D1 . |
|
||||
|
|
|
A2 |
B2 |
C2 |
D2 |
|
|
Перпендикулярность |
|
|
|
|
|
|
|
|
N2 |
N1 N2 A1A2 B1B2 C1C2 0 |
|||||||
N1 |
|
|
|
|
|
|
|
|
Пересечение под углом |
A1A2 B1B2 C1C2 0 |
|
||||||
|
|
|||||||
|
cos |
N1 N2 |
|
|
|
|||
|
|
|
N1 N2 |
|
|
|
||
|
|
A1A2 B1B2 C1C2 |
|
|||||
|
B2 |
C2 |
A2 B2 C |
|
||||
|
A2 |
2 |
||||||
|
1 |
|
|
1 |
1 |
2 |
2 |
2 |
Расстояние от точки x0, y0,z0 до плоскости Ax By Cz D 0:
d Ax0 By0 Cz0 D .

 A2 B2 C2
A2 B2 C2
28

Уравнения прямой в пространстве
Способ задания прямой |
Вид уравнения |
||
Векторное уравнение прямой, проходящей |
|
||
через точку М параллельно |
заданному |
|
|
вектору s . |
|
|
|
M0 |
s |
|
|
|
M |
r r0 |
t s |
|
|
||
O
s – направляющий вектор прямой
s ||M 0M M 0M t s ,
где t – скалярный множитель (параметр)
Канонические |
уравнения |
|
прямой, |
|
x x0 |
|
|
|
y y0 |
|
|
z z0 |
|
|
|||||||
проходящей |
через |
точку M0 x0, y0,z0 и |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
p |
||||||||||||||||
параллельно вектору s m,n, |
p |
|
|
|
m |
|
|
n |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Параметрические |
|
уравнения |
прямой, |
|
|
x x0 |
mt, |
||||||||||||||
проходящей |
через |
точку |
x0, y0,z0 |
|
|
|
|
|
|
nt, |
|||||||||||
|
|
y y0 |
|||||||||||||||||||
параллельно вектору s m,n, |
p |
|
|
|
|
|
|
|
pt |
||||||||||||
|
|
|
z z0 |
||||||||||||||||||
Прямая как линия пересечения двух |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
непараллельных |
|
плоскостей |
(общие |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
уравнения прямой) |
|
|
|
A x B y C z D 0, |
|||||||||||||||||
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
1 |
|
|
|||||||
|
|
|
2 |
|
A2x B2 y C2z D2 0, |
||||||||||||||||
1 |
|
где |
N1 N2 0 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
l |
|
l 1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уравнение |
прямой |
через |
две |
точки |
x x1 |
|
|
|
y y1 |
|
|
z z1 |
|
||||||||
M1 x1, y1,z1 и M2 x2, y2,z2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
z2 z1 |
|||||||||||||||||
|
|
|
|
|
|
|
x2 x1 |
|
|
y2 y1 |
|
|
|||||||||
29
