1881

5.2. Правила записи и округления результатов измерений

Точность результатов измерений и последующих вычислений при обработке данных должна быть согласована с необходимой точностью результатов измерений. Погрешность результатов измерений следует выражать не более чем двумя значащими цифрами. Две значащие цифры следует давать в двух случаях:

–при проведении высокоточных наблюдений;

–при погрешности, выраженной числом с цифрой старшего разряда 3, например = 22.

При обработке результатов измерений следует пользоваться правилами приближенных вычислений, а округление выполнять по следующим правилам:

1.Округлять результат измерения следует так, чтобы он оканчивался цифрой того же порядка, что и погрешность. Если значение результата измерения оканчивается нулями, то ноль отбрасывается до того разряда, который соответствует разряду погрешности.

Пример: погрешность = 0,0005 м.

После вычислений получены результаты измерения:

2. Если первая из заменяемых нулем или отбрасываемых цифр (слева направо) меньше 5, то остающиеся цифры не изменяются.

Пример: = 0,06; Х = 2,3641 2,36.

3. Если первая из заменяемых нулем или отбрасываемых цифр равна 5, а за ней не следует никаких цифр или нулей, то округление производят до ближайшего четного числа, т.е. четную последнюю оставленную цифру или ноль оставляют без изменений, нечетную увеличивают на единицу.

Пример: = 0,25

Х1 = 1,385 1,38; Х2 = 1,355 1,36.

4. Если первая из заменяемых нулем или отбрасываемых цифр больше или равна 5, но за ней следует отличная от нуля цифра, то последнюю оставленную цифру увеличивают на единицу.

Пример: = 12

Х1 = 236,51 237.

Типичные ошибки записи результата измерения представлены в табл. 5.1.

51

Таблица 5.1 Примеры записи результата

5.3. Обработка многократных измерений постоянных величин

Многократным измерением называется измерение, результатом которого является совокупность возможных значений однократных результатов измерений y1(х), ..., y (х), где 2. Эту совокупность

представим в форме вектора-столбца y (x) = (y1(х), ..., y (х))Т. Множеству возможных векторов соответствует случайный вектор многократных измерений Y (x) = (Y1(x),…, Y (x))T, где — объем многократных измерений.

Таким образом, измеряемая величина х, объем многократных измерений для конкретного СИ (совокупности СИ) в рабочих условиях измерения определяют случайный вектор многократных измерений Y (x). Пару структурных элементов (х, ) называют планом измерения для получения вектора многократных измерений.

Разумеется, вектор многократных измерений содержит больше информации об измеряемой величине х, чем результат однократного измерения. Поэтому его следует использовать для получения оценки дисперсии и более точной оценки измеряемой величины х, т. е. для получения оценок количественных значений величин. В общем случае искомую оценку Z количественного значения величины х можно представить в виде некоторой функции от составляющих вектора многократных измерений

Z(x) = f(Y1(x),…, Y (x)). (5.5)

Как функция случайных аргументов оценка Z является случайной величиной. Вид функциональной зависимости выбирается таким, чтобы удовлетворялись два важных в прикладном отношении требования: во-первых, математическое ожидание оценки Z(x) совпадало бы с истинным значением оцениваемой величины и, во-вторых, дисперсия оценки (обозначим ее Dz) была бы минимальной.

52

Измерительные задачи, имеющие целью получение оценок количественных значений величин на основе вектора многократных измерений, будем называть измерительными задачами первого типа. Эти задачи решаются с использованием шкалы интервалов (метрической шкалы). При х – const план измерения такой задачи имеет вид (х, ).

Рассмотрим отношение, обеспечивающее единство измерений:

На основе только этого отношения множество СИ можно разбить на два класса эквивалентности:

– класс СИ, формирующих результаты измерений, систематическая погрешность которых удовлетворяет отношению (5.6);

– класс СИ, формирующих результаты измерений, систематическая погрешность которых не удовлетворяет отношению (5.6).

Очевидно, что по величине те(х) СИ, принадлежащие первому классу, являются в качественном отношении предпочтительнее СИ, принадлежащих второму классу.

Пусть имеется некоторое СИ, принадлежность которого к классу эквивалентности по величине те(х) неизвестна. Оценка принадлежности СИ к классу эквивалентности выполняется с использованием решающей функции следующего вида:

s(u) = 0 – при u u0 – принимается первый класс СИ;

s(u) = 1 – при u > u0 – принимается второй класс СИ, см. (5.7),

где u0 – параметр решающей функции, и – аргумент решающей функции.

Преобразование, реализуемое выражением (5.7), является алгоритмической шкалой порядка с двумя шкальными значениями.

Рассмотрим величину, которую можно взять в качестве аргумента решающей функции. Структуру однократного результата измерения можно представить в виде

Y(х) = ту(х) + Е= х + те(х) +Е,

где my(x)=M[Y(x)] – математическое ожидание случайной величины

Y(x).

53

Очевидно, что в качестве аргумента решающей функции нужно использовать оценку систематической погрешности. На основе выражения (5.8) ее можно сформировать следующим образом: вместо неизвестного значения величины х использовать ее действительное значение xq, а вместо неизвестного значения математического ожидания ту(х) – его оценку.

Возьмем в качестве оценки величины ту(х) результат измерения Y(х). Тогда получим

Недостатком этой оценки является большой разброс ее возможных значений, обусловленный центрированной случайной состав-

ляющей Е с дисперсией De. Использование такой оценки в решающей функции (5.7) привело бы к большим вероятностям ошибок при оценке принадлежности СИ к классам эквивалентности.

Уменьшить эти вероятности ошибок можно, если в качестве оценки математического ожидания тy(х) использовать оценку, полу-

ченную на основе вектора многократных измерений Y (x), т. е. оценку

Z(x) = f(Y1(x),…, Y (x)).

Если ее выбрать такой, чтобы выполнялись условия

1.M[Z(x)]=my(x),

2.M[Z2(x)]=Dz<De,

то такая оценка будет иметь следующую структуру:

Ме(х) = Z(х) – xq = х + те(х) + Z – xq = те(х) + Z = me(х) + Me ,

где Me = Z – центрированная случайная составляющая оценки

Ме(х).

Дисперсия составляющей Z зависит от объема многократных измерений, т. е. Dz( ). С увеличением объема она уменьшается так,

lim

что Dz( ) = 0. Следовательно, за счет выбора значения можно обеспечить малый разброс возможных значений оценки Ме(х) и, как следствие, малые вероятности ошибок оценки принадлежности к классу эквивалентности.

Рассмотренная измерительная задача обладает следующими особенностями: во-первых, как и измерительная задача первого типа, использует вектор многократных измерений Y(x) и, во-вторых, оцен-

54

ка принадлежности к классу эквивалентности реализуется на основе решающей функции (5.7) с параметром u0. Формирование случайного вектора многократных измерений производится на основе плана измерения (xq, ), а оценка принадлежности к классу эквивалентности – с использованием алгоритмической шкалы порядка, характеризующейся параметром и0.

Измерительные задачи, имеющие целью получение оценки принадлежности объекта измерения к классу эквивалентности на основе вектора многократных измерений и решающей функции, называются измерительными задачами второго типа. Эти задачи решаются с использованием экспериментальной шкалы интервалов и алгоритмической шкалы порядка (наименований). План измерения такой задачи имеет вид (x, , u0).

Алгоритмы обработки многократных измерений представлены более подробно в [Назаров].

Глава 6. ПРИМЕНЕНИЕ ИНФОРМАЦИОННОЙ ТЕОРИИ ДЛЯ ОЦЕНКИ РЕЗУЛЬТАТОВ И ПОГРЕШНОСТЕЙ

ИЗМЕРЕНИЯ

6.1. Основные положения теории информации

Основные положения теории информации были разработаны К. Шенноном: "Основная идея … состоит в том, что с информацией можно обращаться почти так же, как с такими физическими величинами, как масса или энергия".

Любая информация, чтобы быть переданной, должна быть соответственным образом "закодирована", т.е. переведена на язык специальных символов или сигналов.

Одной из задач теории информации является отыскание наиболее экономных методов кодирования, позволяющих передать информацию с помощью минимального количества символов. Эта задача решается с учетом наличия или отсутствия искажений (помех) в канале связи.

Другая типичная задача: имеется источник информации (передатчик), непрерывно вырабатывающий информацию, и канал связи, по которому эта информация передается в другую инстанцию (приемник). Какова должна быть пропускная способность канала связи для того, чтобы канал передавал всю поступающую информацию без задержек и искажений? Чтобы решить подобные задачи, нужно нау-

55

читься измерять количественно объем передаваемой или хранимой информации, пропускную способность каналов связи и их чувствительность к помехам.

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Средства измерений предназначаются для получения измерительной информации и обладают, таким образом, информационными характеристиками. При их нахождении исходят из того, что измеряемая величина обладает неопределенностью до тех пор, пока не произведено ее измерение. Степень неопределенности зависит от ряда факторов.

Рассмотрим некоторую систему X, которая может принимать конечное множество состояний: x1, х2, ..., хп с вероятностями p1, р2,…, рп, где

– вероятность того, что система X примет состояние xi (символом Х xi обозначается событие: система находится в состоянии xi).

n

Очевидно, pi 1 как сумма вероятностей полной группы независи-

i 1

мых событий.

В качестве меры априорной неопределенности системы X (измеряемой случайной дискретной величины X) в теории информации применяется специальная характеристика, называемая энтропией.

Энтропией системы (измеряемой величины) называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

где log – знак двоичного логарифма.

Знак минус перед суммой ставится для того, чтобы энтропия была положительной: вероятности pi меньше единицы и их логарифмы отрицательны.

Непрерывная измеряемая величина X априори имеет неопределенность, характеризуемую значением энтропии

где f(х) – плотность распределения величины X.

56

Энтропия обращается в нуль, когда одно из состояний системы достоверно (вероятность равна единице), а другие – невозможны (вероятности равны нулю).

Если рассмотреть случайную дискретную величину X, которая имеет п равновероятных значений, то вероятность каждого из них будет равна рi=1/п и

H(X) n 1log 1 logn. n n

Таким образом, энтропия системы с равновозможными состояниями равна логарифму числа состояний. При увеличении числа состояний энтропия увеличивается.

Энтропия обладает свойством аддитивности: когда несколько независимых систем объединяются в одну, их энтропии складывают-

ся: H (X, Y)=Н (Х)+Н (Y).

Единицы измерения энтропии зависят от выбора основания логарифма. При использовании десятичных логарифмов энтропия определяется в так называемых десятичных единицах (дит). В случае двоичных логарифмов энтропия выражается в двоичных единицах (бит). На практике удобнее всего пользоваться логарифмами при основании 2, поскольку при этом достигается согласие с применяемой в электронных цифровых вычислительных машинах двоичной системой счисления.

6.2. Энтропия и информация

Рассмотрим некоторую систему X, над которой производится измерение, и оценим информацию, получаемую в результате того, что состояние системы X становится полностью известным (погрешность измерений равна нулю). До проведения измерений априорная энтропия системы была Н(Х), после измерений энтропия стала равной нулю, если в результате измерения мы нашли истинное значение величины. Обозначим Ix информацию, получаемую в результате измерений. Она равна уменьшению энтропии IХ = H(X) – H(X/xи) = 0 или IX = H(X), т. е. количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы.

С учетом формулы (6.2)

57

где рi= р(Х xi). Формула (6.4) означает, что информация Ix есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком.

Действительно, для получения Ix каждое значение log pi (логарифм вероятности i-го значения) со знаком минус множится, на вероятность этого состояния и все такие произведения складываются. Естественно каждое отдельное слагаемое – log рi следует рассматривать как частную информацию, получаемую от отдельного измерения, состоящего в том, что система X находится в состоянии Хi. Обозначим эту информацию Ixi.

Тогда информация Ix представится как средняя (или полная) информация, получаемая от всех возможных отдельных измерений с учетом их вероятностей. Так как все числа рi не больше единицы, то как частнаяинформация Ixi, так и полная Ix, не могут быть отрицательными.

Если все возможные состояния системы одинаково вероятны (p1 = Р2= … =рп=1/п), то частная информация от каждого отдельного измерения Ixi = – log p = log n равна средней (полной) информации

6.3. Применение основных положений теории информации для характеристики процесса измерения

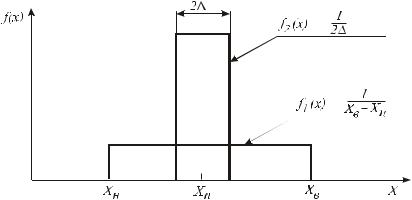
Точность измерений обычно характеризуется числовым значением полученных при измерении или априорно известных погрешностей измерений.Если предположить, что плотность распределения различных значений измеряемой величины вдоль всей шкалы средства измерения одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределенияплотностиf1(x)вдоль шкалызначений (рис.6.1).

Рис. 6.1. Плотность распределения данного средства измерения

58

Пусть в результате однократного измерения значения измеряемой величины X результат измерения равен хи. Если известно, что средство измерения имеет случайную абсолютную погрешность в пределах ± , то не следует утверждать, что действительное значение измеряемой величины равно хи. Можно лишь утверждать, что это значение лежит в полосе xи ± . Незнание истинного значения измеряемой величины сохраняется после получения результата измерения хи, но теперь оно характеризуется не исходной энтропией Н(Х), а лишь энтропией разброса действительного значения X величины относительно полученного результата xи. Эта условная энтропия Н(Х/хи) определяется погрешностью данного средства измерения.

В теории информации факт проведения измерений в диапазоне от Хн до Хв означает, что при использовании данного средства измерения может быть получен результат измерений xи только в пределах от Хн до Хв. Другими словами, вероятность получения значений хи, меньших Хн и больших Хв, равна нулю. Вероятность же получения результата хи в пределах от Хн до Хв равна единице.

Поскольку вероятность получения результата измерений xи в пределах от Хн до Хв равна единице, то площадь под кривой f1 (x) должна быть равна единице. При равномерном распределении плотности вероятности

ства измерения (± ) действительное значение измеряемой величины X лежит в пределах от Хи – до Хи + , т. е. в пределах участка 2 .

С информационной точки зрения интерпретация результата измерения состоит в том, чтобы область неопределенности простиралась от Хн до Xв и характеризовалась сравнительно небольшой плотностью распределения f1(x). После измерения неопределенность уменьшилась до величины 2 , а плотность распределения увеличилась до величины f2(x) с учетом того, что (Xв –Xн), что и отражено на рис. 6.1.

Получение какой-либо информации об интересующей нас величине заключается в конечном счете в уменьшении неопределенности

59

В нашем примере с равномерным законом распределения

Данная операция, которая обычно используется при определении относительной погрешности измерения, характеризует один из основных приемов анализа информационных свойств измерений.

Глава 7. ОРГАНИЗАЦИОННО-ПРАВОВЫЕ ОСНОВЫ МЕТРОЛОГИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ

7.1. Государственная система обеспечения единства

измерений (ГСИ)

Государственная система обеспечения единства измерений (ГСИ) представляет собой комплекс нормативных документов межрегионального и межотраслевого уровней, устанавливающих правила, нормы, требования, направленные на достижение и поддержание единства измерений в стране.

Согласно закону РФ «Об обеспечении единства измерений» «единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах величин и погрешности измерения не выходят за установленные границы с заданной вероятностью».

Единство измерений необходимо для того, чтобы можно было сопоставлять результаты измерений, выполненных в разных местах, в различное время с помощью разнообразных приборов. Единство измерений обеспечивает взаимозаменяемость изделий, например, деталей, изготавливаемых по одному чертежу на разных предприятиях.

Основным нормативным документом ГСИ является Закон РФ «Об обеспечении единства измерений». На его основе разрабатываются нормативные документы, конкретизирующие общие требования закона применительно к отдельным отраслям народного хозяйства, областям измерений и методикам выполнения измерений.

60