
- •Введение
- •1. ИЗГИБ ПРЯМОУГОЛЬНОЙ ГИБКОЙ ПЛАСТИНЫ
- •1.1. Деформации
- •1.2. Уравнения равновесия
- •1.3. Физические уравнения
- •1.4. Система разрешающих уравнений
- •1.5. Граничные условия
- •1.6. Метод последовательных приближений
- •1.7. Пример 1
- •1.8. Пример 2
- •2. ПРЕДЕЛЬНОЕ СОСТОЯНИЕ РАМЫ
- •2.1. Постановка задачи
- •2.2. Пример 1
- •2.3. Пример 2
- •2.4. Пример 3
- •Список рекомендуемой литературы

Шаг 1. Сначала векторы w , |
принимаем равными нулю и ре- |
||||||||
шаем уравнения (24) с определением всех компонентов wmn вектора |
|||||||||
w как для жесткой пластинки. |
|
|
|
||||||
Шаг 2. Полученный вектор w подставляется в уравнение (23) |
|||||||||
и вычисляется каждый компонент ij вектора , при этом матрица |
|||||||||
Aij , соответствующая ij , должна быть уже подготовлена. |
|||||||||
Шаг 3. Теперь векторы w , , найденные в первом приближе- |
|||||||||
нии, подставляются в уравнения (24) с заранее подготовленными мат- |
|||||||||
рицами Bmn , затем вычисляются элементы wmn |
и из них формиру- |
||||||||
ется обновленный вектор w . |
|
|
|
|
|||||
Шаг 4. Процесс повторяется, начиная с шага 2, или заканчива- |
|||||||||
ется, если разница между векторами w , ( ,) вычисленными на теку- |
|||||||||
щем шаге и предыдущем, составляет малую долю от длины вектора |
|||||||||
w , ( ). |
|
|
|
|
|
|
|
|
|
После завершения процесса последовательных приближений |
|||||||||
компоненты wmn , ij векторов w , оказываются известными и ис- |
|||||||||
|
|
|
|
|
|
|
И |
||
пользуются в двойных тригонометрических рядах (22), аппроксими- |
|||||||||
рующих функцию прогибов w и функцию напряжений . Эти уже |
|||||||||
|
|
|
|
|
|
Д |
|
||
известные функции в дальнейшем используются для вычисления про- |
|||||||||
гибов, изгибающих моментов (19), продольных сил (20) в конкрет- |
|||||||||
ных сечениях пласт нки. |
|
А |
|
|
|||||
|
|
|
|
|
1.7. Пример 1 |
|
|||
|
|
|
|
б |
|
|
|
||
Изгиб квадратной в плане пластины с |
|
||||||||
|
|
|
и |
|
|
|
|
||
распределенной нагрузкой. Размеры в плане |
|
||||||||
пластины a 1,0 |
м, b a 1,0 м, |
толщина |
|
||||||
0,01 |
м, |
модуль |
упругости |
a |
|||||
|
|||||||||
|
|
С |
|
|
|
|
0.875 a |
||
E 210ГПа, |
коэффициент |
Пуассона |
|||||||
|
|||||||||
0,2. |
|
Равномерно распределенная |
на- |
|
|||||
грузка |
интенсивностью |
q 65,2кН/м2 |
0.875 a |
||||||
размещена на квадратной площадке с раз- |
a |
||||||||
Рис.4 |
|||||||||
мерами |
|
c (14/16)a 0,875м. |
Центр |
||||||
|
|
||||||||
площадки совпадает с центром плана пластинки (рис.4). Пластинка по |
|||||||||
всем четырем кромкам шарнирно оперта. |
|
|
|||||||
Для определения изгибающих моментов и внутренних усилий в |
|||||||||
пластинке сначала необходимо найти функцию прогибов и функцию |
|||||||||
11
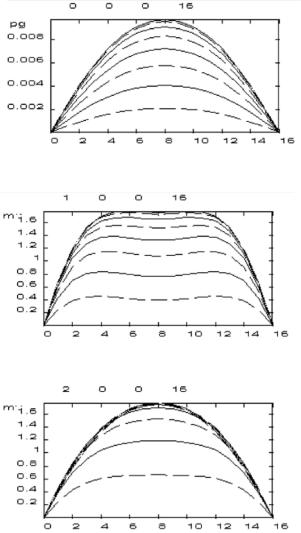
напряжений. Функцию прогибов и функцию напряжений представим в виде двойных тригонометрических рядов (22), коэффициенты которых вычисляются из системы уравнений (23), (24) последовательно по шагам, представленным выше. Индексы искомых коэффициентов
wmn , ij рядов (23), (24) изменяются в |
пределах |
от 1 до |
I J M N 10 включительно. Таким образом, количество коэф- |
||
фициентов каждого ряда равно M N 100, |
I J 100. |
Поэтому |
матрицы Aij , Bmn – квадратные, содержат каждая по 100 столбцов и по 100 строк, при этом матрицы с различными индексами различны, т.е. Aij Akl , Bmn Bpq . Эти матрицы можно не хранить, а вычислять од-
новременно с вычислениями вторых слагаемых в левой части каждого из
уравнений системы (23), (24). В данном расчете количество повторений |
|
шагов 2 и 3 |
И |
было выполнено 200. Далее выполняется расчет прогибов и |
|
внутренних усилий с построением соответствующих эпюр, показанных |
||||||||
, |
|
|
|
Д |
|
|
|
|
|
|
|
|
нарис.5–11. |
|
|
|
|
, |
|
|
|
На рис. 5 приведены эпю- |
||||
|
|
|
А |
|
|
|
|
|
, |
|
|
|
ры прогибов пластинки по ли- |
||||
|
|
|
ниям, параллельным оси |
x , |
с |
|||
, |
|
|
|
|||||
|
б |
шагом между ними, равным |
||||||
|
|
|||||||
|
|
a/16. Как видно из рисунка, |
||||||
|
|
|
|
|||||
|
|
|
|
прогибы симметричны относи- |
||||
|
Рис.5 |
|
|
тельно |
центральных осей пла- |
|||
, |
С |
|
|
стинки. |
Максимальный прогиб |
|||
, |
и |
|
равен |
wmax 0,009748 м. |
||||
, |
|
Прогиб примерно равен толщи- |
||||||
, |
|
|||||||
, |
|
|
|
не пластинки 0,01м. |
|
|
||
|
|
|
На рис. 6 даны эпюры из- |
|||||
, |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
, |
|
|
|
гибающих моментов Mx |
на ли- |
|||
|
|
|
|
|||||
|
Рис.6. |
|
|
ниях, ориентированных |
также |
|||
|
|
|
как эпюры прогибов, а на рис. 7 |
|||||
|
|
|
|
– моментов My . Ординаты |
||||
, |
|
|
|
обеих эпюр вычислены в узлах |
||||
, |
|
|
|
сетки, наложенной на пластин- |
||||
, |
|
|
|
|||||
, |
|
|
|
ку (см. рис. 4). Значения момен- |
||||
, |
|
|
|
тов Mx |
и My |
в узлах |
сетки |
|
, |
|
|
|
|||||
, |
|
|
|
совпадут, если одну из вычис- |
||||
|
|
|
|
|||||
|
Рис.7 |
|
|
ленных |
таблиц |
повернуть |
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|

Рис.8 |
Рис.9 |
плане на 900. Максимальные |
одинаковы Mxmax Mymax 1,772 |
значения моментов Mx , My |
|
кН.м/м, но в центре пластинки |
Mx My 1,755 кН.м/м. 17 эпюр |
крутящих моментов H приведены на рис. 8. Наибольшие крутящие моменты H 1.846 кН.м/м возникают в углах контура пластинки.
никают в центре пластины и равны Nxmax ИNymax 2947,15 кН/м.
Эпюры нормальных Nx , Ny и сдвигающих S сил показаны на
рис.9–11. Максимальные значения нормальных сил (см. рис.9,10) воз-
Сдвигающие усилия S (рис. 11) достигают наибольших значений у кромок пластинки вблизи ее углов и равны S 2292,52 кН/м. Сле-
дует отметить, что вблизи краев пластины нормальные усилия оказы- |
|||
ваются сжимающими, но по величинеДнезначительны. |
|||
|
|
А |
|
|
б |
|
|
и |
|
|
|
Рис.10 |
|
|
Рис. 11 |
С |
|
|
|
1.8. Пример 2
Изгиб прямоугольной пластины с распределенной нагрузкой, действующей на ограниченном прямоугольном участке.
Нагрузка расположена несимметрично относительно центральных осей пластины (рис.12). Размеры в плане пластины a 1,0 м, b 0,75 м, толщина 0,01 м, интенсивность распределенной на-
грузки q 521,6кН/м2 , модуль упругости E 210ГПа, коэффициент Пуассона 0,2. Нагрузка размещена на площадке с размера-
13

ми 0,375 0,25м2 . Центр площадки не совпадает с центром плана пластинки (см. рис.12). Координаты углов площадки показаны на ри-
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сунке |
x1 0,25a, |
x2 0,625a , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y1 b/6, y2 b/2. Ячейки наложен- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b/2 |
|
|
|
|
|
ной сетки квадратные. Шаг сетки равен |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/16 м. Пластинка по всем четы- |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b/3 |
|
b |
|
|
рем кромкам шарнирно оперта. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет |
выполнен |
так же, как в |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b/6 |
|
|
|
|
x |
примере 1, |
с использованием двойных |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0.25 a |
x1 |
0.375 a |
x2 |
0.375 a |
|
|
|
|
|
|
|
тригонометрических рядов для аппрок- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
|
|
|
|
|
симации функции прогибов и функции |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряжений. Индексы искомых коэф- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
фициентов wmn , ij |
рядов |
(15), |
|
И |
в пределах до |
|||||||||||||||||||||||||||||
(16) изменяются |
||||||||||||||||||||||||||||||||||
I J M N 10 включительно. Эпюры прогибов, в количестве 11, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
показаны на рис.13. Наибольший прогиб |
wmax 1,007cм в точке с |
|||||||||||||||||||||||||||||||||
координатами x 7 ,y 5 . Как видно из рисунка, эпюры прогибов |
||||||
|
|
|
|
|
А |
|
несимметричны относительно середины пластинки. |
||||||
|
Эпюры моментов Mx , My |
показаны на рис. 14–15 с максимума- |
||||
ми Mxmax 3,237 |
|
б |
||||
кН.м/м, |
Mymax 5,146 кН.м/м. Максимальные |
|||||
, |
|
и |
|
|
H , согласно рис. 16, действуют на |
|
значения крутящих |
моментов |
|
||||
кромках пластинки (Hmax 2,719 кН.м/м). |
||||||
, |
С |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
Рис. 13 |
|
|
|
Рис.14 |
|
Рис.15 |
Рис.16 |
14
