1608

Л.А. УСОЛЬЦЕВ

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Учебное пособие

Омск 2008

Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия

( СибАДИ)

Л.А. Усольцев

ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Учебное пособие

Омск Издательство СибАДИ

2008

1

УДК 519.852 ББК 22.183.4

У 76

Рецензенты:

д-р воен. наук, проф. А.А.,Колокольников ; д-р воен. наук, проф. В.А.Рябошапко

Работа одобрена редакционно-издательским советом академии в качестве учебного пособия по дисциплине «Прикладная математика» для студентов дневной формы обучения.

Усольцев Л.А.

У76. Линейное программирование: Учебное пособие.-- Омск: Изд-во СибАДИ, 2008.–85с.

Пособие составлено на основании рабочей программы дисциплины «Прикладная математика» и предназначено для студентов дневной формы обучения СибАДИ.

Рассмотрены типовые задачи линейного программирования, в частности, транспортная задача, задачи о назначениях, оптимальном раскрое материала, оптимальном распределении ресурсов, диете, коммивояжере и упаковках. Дана общая постановка, геометрическая интерпретация области допустимых решений и определение оптимального решения задачи линейного программирования симплекс-методом. Кроме того, приведены методики решения транспортной задачи методами северо-западного угла, минимальной стоимости и потенциалов. Изложение материала ведётся на примерах решения прикладных инженерных задач.

Табл. 17. Ил. 5. Библиогр.: 10 назв.

2

ГЛАВА 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

Раздел математического программирования, изучающий задачи отыскания максимума (минимума) линейной функции цели при линейных ограничениях в виде равенств и неравенств, называется линейным программированием. Одним из основных общих условий оптимизации является возможность выбора решения из некоторого допустимого множества. Применительно к задаче линейного программирования это означает, что число неизвестных в ней должно быть больше числа ограничений.

1.1. Постановка задачи

Общая задача линейного программирования формулируется следующим образом: найти максимум (минимум) линейной функции цели для n переменных x1, x2 ,...xi ,...xn

заданные числа.

Задача минимизации функции (1) сводится к задаче её максимизации путем замены знаков всех коэффициентов c j на

противоположные. Линейное программирование является наиболее развитой законченной областью математического программирования. Общая постановка задачи линейного программирования и один из подходов к ее решению (идея разрешающих множителей или

3

двойственных оценок) впервые приведены в работе российского ученого Л.В.Канторовича в 1939 г. В этой работе намечен один из методов решения задачи – метод последовательного сокращения невязок. В работе Л.В. Канторовича и М.К. Гавурина, выполненных в 1940г., применительно к транспортной задаче разработан еще один метод решения задачи линейного программирования, получивший название метода потенциалов.

Бурное развитие линейное программирование получило с появлением компьютерной техники и ее использованием для решения экономических задач. Началом этого развития послужила разработка американским ученым Дж.-Б. Данцигом в 1947 г. эффективного метода решения задачи линейного программирования, получившего название симплекс-метода. Этот метод является обобщением метода потенциалов на общую задачу линейного программирования, но разработан независимо от него. Позднее был разработан еще один – двойственный симплекс-метод, который по существу является симплекс-методом для решения двойственной задачи линейного программирования, но формулируется в терминах исходной задачи. Отмеченные методы являются конечными. Кроме них, для решения задачи линейного программирования используются интерактивные методы, дающие за конечное число шагов лишь приближенное (с заданной степенью точности) решение. Тесная связь между линейным программированием и теорией игр позволяет использовать численные методы теории игр для решения задачи линейного программирования.

Другая группа интерактивных методов характеризуется заменой исходной задачи на эквивалентную ей выпуклую экстремальную задачу без ограничений, для решения которой используются различные градиентные методы.

Для решения задач большой размерности разработаны методы декомпозиции. Эти методы дают возможность вместо исходной задачи решать последовательность задач меньшего размера, позволяющие обойти трудности, связанные хотя и со значительными, но все-таки ограниченными (конечными) объемами оперативной памяти компьютера.

Вместе с тем, методы линейного программирования недостаточны при решении задач с дополнительными ограничениями на целочисленность значений переменных. Изучением таких задач занимается целочисленное (дискретное) программирование.

4

Экономичные методы решения задач линейного программирования, коэффициенты которых зависят от параметров, разрабатываются в

параметрическом программировании. Изучаются также, наряду с общей, частные задачи линейного программирования, такие как транспортные, распределительные задачи, задачи теории расписаний, выбора и другие. Некоторые идеи линейного программирования используются в теории наилучших приближений, теории моментов и других разделах математики.

В терминах задачи линейного программирования формулируются с достаточной степенью точности многие проблемы оперативного и перспективного планирования и управления разнообразными производствами и технологическими процессами, организации бесперебойной и целенаправленной работы комплексов и отдельных агрегатов.

Типичным примером задачи линейного программирования является задача планирования работы предприятия, выпускающего некоторый однородный продукт. Задача ставится следующим образом: имеется n различных технологий и m ресурсов (транспорт, рабочая сила, сырье, энергия и т.д.) производства. Известны:

c j – количество единиц продукта, которое можно получить при

использовании j-ой технологии в единицу времени (j=1,…,n);

aij – расход i-го ресурса при использовании j-ой технологии

(i=1,…, m; j=1,…,n);

bi общий запас i-го ресурса (i=1,…,m);

x j время, в течение которого производство ведется по j-ой технологии. Требуется отыскать план X (x1,...xn ) , при котором из

имеющихся ресурсов выпускалось бы максимальное количество продукта.

Математически эта задача формулируется в виде (1), (2), (4) при m1 n , n1 n . Каждой задаче линейного программирования

соответствует двойственная задача, переменные и ограничения которой также имеют экономическую интерпретацию.

Любую задачу линейного программирования можно представить в каноническом виде, когда все ограничения, кроме условий неотрицательности переменных, должны быть равенствами

j 1

5

Ограничения (6) часто записываются в векторной форме:

направлений.

Вектор X x1,...,xn , удовлетворяющий уравнениям (6) и (7),

называется планом задачи.

План, на котором линейная форма принимает максимальное значение, называется оптимальным планом (или решением) задачи.

1.2. Геометрическая интерпретация задачи линейного программирования

Для того, чтобы познакомиться с некоторыми понятиями линейного программирования, разберем конкретный пример.

Пусть задана целевая функция

и система ограничений

Представим рассматриваемую задачу графически в декартовой системе координат. Для этого определяем максимальные величины

X1 X 2 =35, чтобы перекрыть расчетные величины (25 и 35).

x2

35

9

30

25

20 A

10

15

10 B

11

5

0

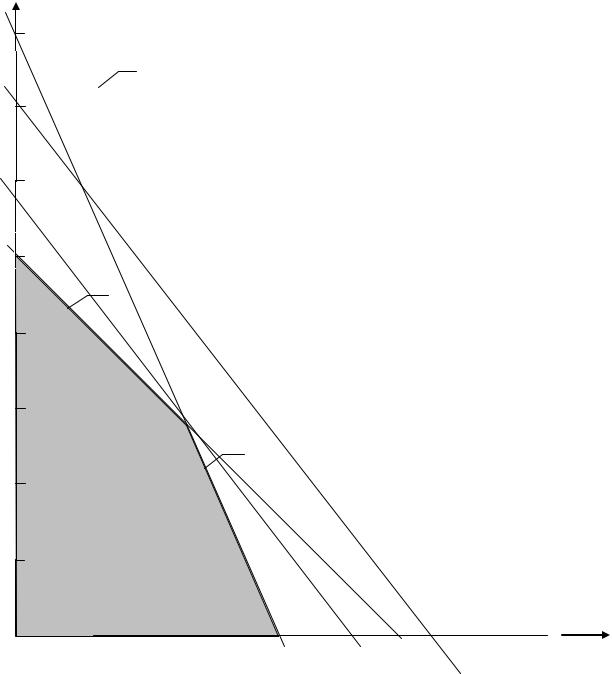
Рис. 1. Геометрическая интерпретация задачи линейного программирования

Все соотношения (9) (13) – это прямые линии, которые строим

7

по двум точкам. Рассмотрим это построение на примере соотношения (10): 4x1 5x2 100 . Определим координаты первой из двух точек, по которым затем построим искомую прямую (10). Допустим, что x1 =0 (для того, чтобы искомые точки располагались по осям

координат, принимаем этот вариант), тогда x2 1005 20 . Если x2 0 ,

то x1 1004 25 . Итак, точки для построения прямой по соотношению

(10) будут иметь координаты (0;20) и (25;0), которые наносим на график (см. рис. 1) и соединяем между собой прямой линией (10). Необходимо определить, с какой стороны от этой линии располагается область допустимых решений. Для этого используем следующую методику: выбираем произвольную точку по одну из сторон от этой линии. Допустим, точку x1 x2 0. Подставляем

координаты этой точки в соответствующее соотношение (10). Если рассматриваемая точка удовлетворяет соотношению (10), то область допустимых решений лежит с той же стороны, что и рассматриваемая точка. В противном случае – в противоположной полуплоскости. В рассматриваемом случае точка x1 x2 0 лежит

слева от прямой линии (10) и удовлетворяет условию (10): 4 0 + 5 0 100 (0 < 100). Значит и область допустимых решений лежит слева от прямой (10). По аналогии построим прямую (11): первая точка –

на график и соединяем прямой линией (см. рис. 1). Определяем, используя вышеуказанную методику, что область допустимых решений лежит слева от прямой (11).

Прямые линии 12 и 13 строить не нужно, т.к. они уже построены: прямая 12 – это ось ординат, а прямая 13 – это ось абсцисс. Причем область допустимых решений для прямой 12 находится справа от нее, а для прямой 13 – выше оси абсцисс. Таким образом, область допустимых решений (ОДР) для рассматриваемого примера представляет собой многогранник ABCD (см. рис. 1, затемненная область).

Для графического решения рассматриваемой задачи необходимо построить линию, соответствующую целевой функции (9). В зависимости от значений x1 и x2 целевая функция (9) представляет

собой не одну единственную линию, как ограничения (10) (13), а

8

практически бесконечное множество параллельных линий, ориентированных определенным образом в системе координат. Чтобы определить углы наклона целевой функции (9) к осям координат, необходимо построить любую из такого множества параллельных линий, соответствующих целевой функции (9). Для того, чтобы определить две будущие точки, соединив которые прямой линией, мы получим линию целевой функции, приравниваем целевую функцию (9) к определенной величине. Эту величину выбираем из условия, чтобы при построении будущей линии 9 не выйти за максимальные пределы величин x1 и x2 , принятых по осям

координат. Чтобы выполнить это условие, умножаем минимальный коэффициент функции (9) – это величина 9 на величину 30 и в результате получаем 9 30=270, к которой приравниваем целевую функцию (9).

Имеем R(x) 10x1 9,2x2 270.

Тогда, если x1 0 , то x2 30 , а если x2 0 , то x1 27. Наносим эти точки на график (см. рис. 1) и соединяем их прямой линией.

Теперь, чтобы определить графическое решение рассматриваемой задачи, необходимо прямую 9 максимально удалить от начала координат, но при этом необходимо, чтобы прямая 9 имела хотя бы одну общую точку с ОДР.

Как видно на графике (см. рис. 1), решение, согласно изложенному правилу, лежит в точке B с координатами x1 12 и

x2 8,5 . Точность графического решения задачи в значительной степени зависит от выбранных масштабов по осям координат и точности соответствующих построений. Но в любом случае более точное решение задачи линейного программирования можно получить, решив ее одним из математических методов.

Свойства области допустимых решений (ОДР):

1.ОДР всегда замкнута.

2.ОДР всегда выпукла. Для двумерного пространства это означает, что ОДР всегда лежит по одну сторону от линии, ее ограничивающей. Для многомерного – от гиперплоскости, ее ограничивающей.

3.Решение задачи линейного программирования находится либо

водной из вершин многогранника ОДР и тогда оно единственно,

9