
1494
.pdf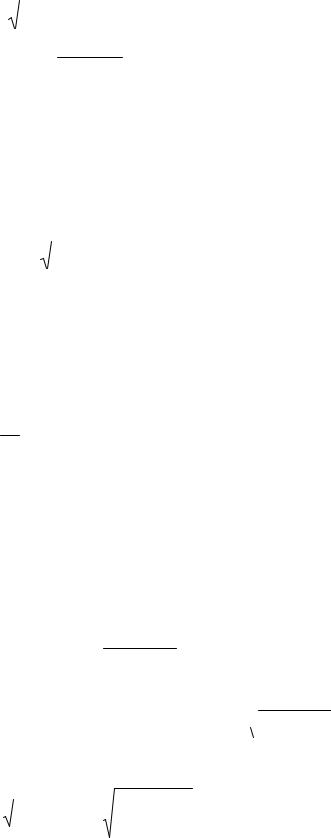
qm |
|
Em |
|
, |
|
|
|
|
|||
L 4 2 2 ( 2 02)2 |
|||||
|
|
|
|||
2 tg 2 02 .
Продифференцировав qm по времени, найдём силу тока в контуре при
установившихся колебаниях: |
|
|
|
|
|
|
|
||
I |
dq |
qm sin( t ) Im cos( t |
|
), |
|
||||
|
|
|
|||||||
|
dt |
|
|
2 |
|
|
|||
где |
|
Em |
|
|
|
|
|
||
|
Im qm |
|
|
. |
|
|
(8) |
||
|
|
|
|
|
|
||||
|
L 4 2 2 ( 2 02)2 |
|
|
||||||
|
|
|
|
|
|
|
|
||
При последовательном соединении элементов в электрической цепи ток в каждом элементе одинаков, тогда
UR ImRcos( t |
|
), |
|
||||
|
|
||||||
|
|
2 |
|
|
|||
UC |
qm |
cos( t ) |
Im |
cos( t ), |
(9) |
||
C |
|
||||||
|
|
C |
|
||||
UL L dI LIm cos( t ). dt
Таким образом, изменения q, I , UR , UC , UL происходят по гармоническому закону с частотой внешней ЭДС. Амплитуды их колебаний зависят от частоты вынуждающей ЭДС и при определенных её значениях достигают максимумов. Это явление называется резонансом, а соответствующее значение частоты – резонансной частотой рез .
Для определения резонансной частоты необходимо продифференцировать любое из амплитудных значений qm, Im, URm , UCm или ULm пои приравнять полученное нулю. Получим
1 0, 2,3 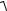
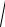 02 2 2 .
02 2 2 .
Значение 1 0 определяет минимальные значения величин, отри-
цательное значение не имеет физического смысла, а 
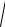 02 2 2
02 2 2
устанавливает максимальное значение амплитуд, т е. это резонансная частота:
|
|
|
|
|
1 |
|
R |
2 |
|
|
|
2 |
2 |
2 |
|
|
|
||||
рез |
0 |
|
= |
|
|
|
|
. |
(10) |
|
|
LC |
|
|
|||||||
|
|
|
|
|
|
2L2 |
|
|||
Графики зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы представляют собой резонансные кривые. Резо-
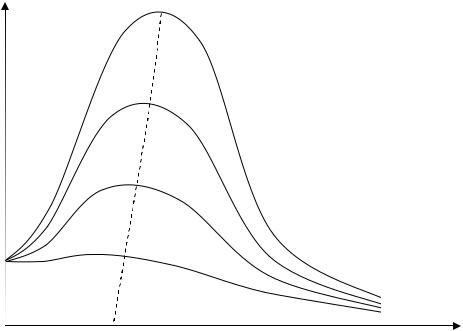
нансные кривые для амплитуды напряжения на конденсаторе приведены на рис. 2.
UСm
β1
β2
β3
Em
β4
Ω
Ωрез
Рис. 2. Резонансные кривые для UCm: β1 < β2 < β3 < β4
Отдельные кривые на графике соответствуют различным значениям коэффициента затухания . Чем меньше , тем выше и правее максимум кри-
вой. При большом затухании, когда 2 02, резонанса не происходит; с увеличением частоты амплитуда монотонно убывает (кривая 4) до нуля. При стремлении к нулю резонансные кривые сходятся в одной точке, имеющей значение напряжения на конденсаторе при подключении его к источнику постоянного тока с напряжением Em. При малом затухании
( 2 02) резонансная частота практически равна собственной частоте свободных колебаний рез 0.
Резонансные кривые для силы тока Im приведены на рис. 3.
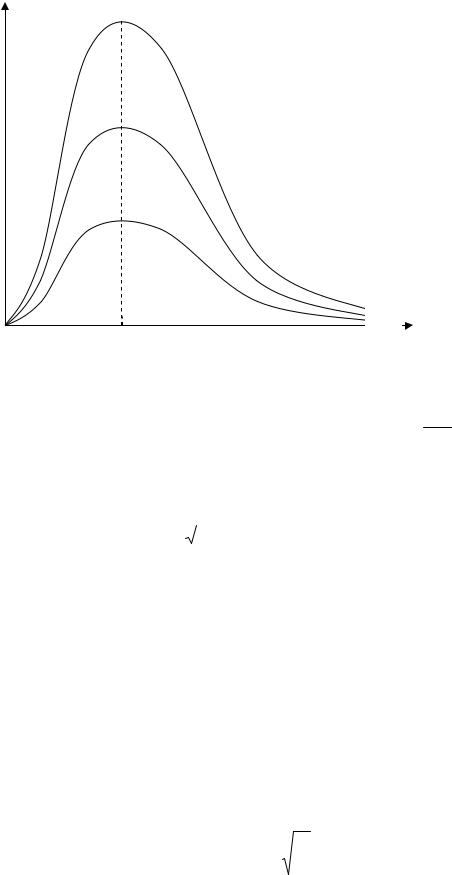
Im
β3
β2
β1
Ω
Ωрез
Рис. 3. Резонансные кривые для силы тока: β1 < β2 < β3
Амплитуда тока имеет максимальное значение, если L 1 , т. е.
C
резонансная частота силы тока совпадает с собственной частотой контура
0 :
рез |
|
|
1 |
|
|
0. |
|
|
|
|
|
||||
|
|
||||||
|
|
|
LC |
||||
Таким образом, при последовательном соединении элементов цепи |
|||||||
(см. рис. 1) амплитуда силы тока |
Im |
Um |
, а разность фаз =0, т. е. при |
||||
|
|||||||
|
|
|
|
|
|
R |
|
этой частоте напряжения на ёмкости UC и на индуктивности UL полностью компенсируют друг друга, поскольку равны по величине и противоположны по фазе. При этом напряжения UCm и ULm могут значительно превышать напряжение, приложенное к цепи Um. Поэтому этот резонанс в цепи с последовательно включенными L, C, R и переменной ЭДС называют резонансом напряжений.
При вынужденных колебаниях весь процесс характеризуется собственной частотой 0 , логарифмическим декрементом затухания и добротностью системы Q, которые связаны между собой соотношениями
T |
R |
∙ |
2 |
|
R |
R |
C |
; |
(11) |
|
2L |
|
0 |
L 0 |
|
L |
|
||

Q |
|
|
L 0 |
|
1 |
|
L |
. |
(12) |
|
|
|
|
R R C
Амплитуда резонансного напряжения на конденсаторе UCрез в отно-
шении к амплитуде внешнего напряжения:
UСрез |
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
1 |
|
1 |
|
|
|
1 L |
Q, |
|
||||
|
/ ImR |
|
|
LC |
(13) |
||||||||||
Еm |
|
|
RC 0 |
|
|
|
|
|
|||||||
|
|
|
|
R C |
|||||||||||
|
0C |
|
RC |
|
|
||||||||||
т. е. добротность определяет во сколько раз резонансное напряжение превышает внешнее напряжение. Таким образом, чем выше добротность контура, тем уже резонансная кривая. Ширина резонансной кривой определя-
ется разностью частот на уровне Iрез , а острота резонансной кривой
 2
2
отношением рез .
|
I |
рез |
|
|
|
|
|||
Полагая в (8) Im |
E0 |
R 2 и определяя для этого значения |
|||||||
|
|
|
|
||||||
2 |
|
||||||||
|
|
|
|
|
|
|
|||
тока частоты вынужденных колебаний, установим, что
рез |
|
|
0 |
Q. |
(14) |
|
|
|
|||
|
|
|
|||
Таким образом, построенные резонансные кривые для силы тока по ширине кривой и резонансной частоте 0 позволяют определить добротность Q контура (14), с помощью которой при известном сопротивле-
нии в цепи найдём из (12) индуктивность катушки контура: |
|
L RQ |
(15) |
0
и также из (12) находим ёмкость конденсатора |
|
||
C |
1 |
. |
(16) |
|
|||
0RQ |
|
||
Варьируя активным сопротивлением Ra и учитывая, что R Ra RL, найдём сопротивление катушки RL :
RL |
|
R2Q2 R1Q1 |
. |
(17) |
|
||||
|
|
Q1 Q2 |
|
|
ВЫПОЛНЕНИЕ РАБОТЫ
1.Вызвать приборную панель лабораторной работы.
2.На приборной панели включить панель нажатием на кнопку «Вкл» и генератор синусоидальных колебаний «Питание».
3.Откалибровать нули осциллографов. Для этого бегунками «про- гресс-баров» выбрать такое положение, чтобы сигналы осциллографов при замыкании выводов размещались точно по центру окон осциллографов.
4.Собрать цепь, представленную на рис. 4, состоящую из последовательно соединённых катушки индуктивности L, конденсатора емкостью C, активного сопротивления Ra и генератора синусоидальных колебаний
Г.
C
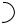 L
L
R
˜Г |
N1 |
N2 |
Рис. 4. Схема соединения элементов колебательного контура
5. Установить рукоятку управления резистором в среднее положе-
ние.
6.Вращая мышью рукоятку «Частота» на экране монитора, убедиться в наличии резонанса.
7.Снять зависимость амплитуды тока Im от частоты в интервале
частот больших и меньших резонансной. Для этого, установив частоту, взять мышью измерительные скобки, находящиеся в левых верхнем и нижнем углах экрана осциллографа, подвести их к верхнему и нижнему максимумам синусоиды. После этого нажать мышью кнопку «Данные» для передачи данных в таблицу. Для очистки таблицы следует нажать правую кнопку мыши. В меню выбрать строку «Очистить журнал» и щёлкнуть по ней левой кнопкой.
№ |
|
Ra1=0,4 кOм |
|
|
|
Ra2=0,8 кOм |
|
ν, Гц Im Q1 RL |
L |
C |
ν, Гц Im Q2 RL L |
C |
|||

8. Рукоятку Ra перевести в крайнее правое положение и повторить измерения по п. 7.
9.Построить резонансные кривые Im = Im (Ω).
10.По графикам определить резонансную частоту 0 , ширину резо-
нансной кривой и вычислить добротности Q1 и Q2 при Ra1 и Ra2.
11.Определить сопротивление катушки индуктивности RL, согласно (17), а также индуктивность катушки L и ёмкость конденсатора C, исполь-
зуя (15) и (16).
12.Рассчитать погрешности найденных величин.
Контрольные вопросы
1.Какие колебания называются вынужденными?
2.Какими параметрами характеризуются вынужденные колебания?
3.Как определяется добротность контура в настоящей работе?
4.Из чего складывается полное сопротивление контура?
5.Возможно ли получение на отдельных элементах контура напряжения, во много раз большего приложенного напряжения?
6.Чем определяется разность фаз между током и приложенным напряжением?
7.Что происходит на частоте резонанса в контуре, если R стремится
кнулю?
Лабораторная работа № 4
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ
Цель работы – изучить работу колебательного контура, свободные затухающие электромагнитные колебания и их характеристики.
Приборы и принадлежности: комплекс реально-виртуальной лаборатории по электричеству и электромагнетизму (РВЛ ЭиЭ).
ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Для возбуждения и поддержания электромагнитных колебаний используют колебательный контур, представляющий собой замкнутую цепь, которая состоит из последовательно соединенных конденсатора емкостью С, ка-
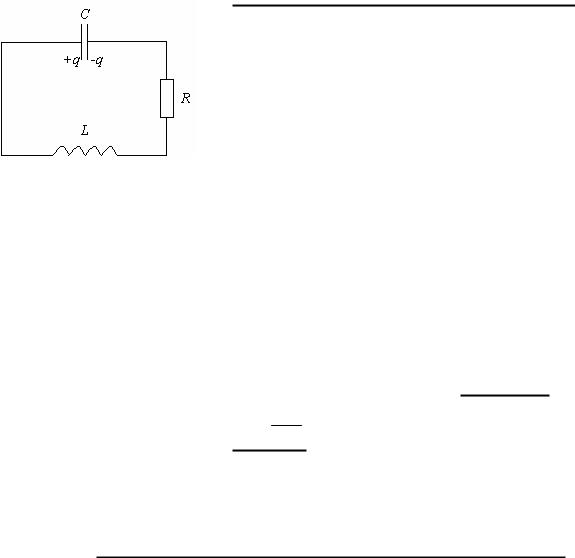
тушки индуктивности L и омического (активного) сопротивления R. Омическое сопротивление является суммой сопротивлений соединительных проводов, провода катушки индуктивности и включённого в контур резистора. Принципиальная схема колебательного контура приведена на рис. 1.
Рассмотрим, как возникают ко- лебания в контуре. В начальный момент с помощью генератора одиночных импульсов конденсатор заряжается до некоторой разности потенциалов на его обкладках U. При этом обкладкам конденсатора сообщен зарядq, а энергия электрического поля конденса-
|
|
CU |
2 |
|
|
тора W |
|
0 |
. |
||
2 |
|
||||
Рис. 1. Колебательный кон- |
|
|
|
|
|
Если теперь генератор отключить, а конденсатор замкнуть на катушку с индуктивностью L, то начнется его разрядка и в катушке возникает ток. Этот возрастающий от нуля ток приводит к возникновению магнитного поля. Следовательно, энергия электрического поля между обкладками конденсатора постепенно переходит в энергию магнитного поля катушки. В момент полной разрядки конденсатора ток в катушке достигает максимального значения I0 и энергия
магнитного поля W LI02 . В момент полной разрядки кон-
2
денсатора ток в катушке, казалось бы, должен прекратиться. Однако уменьшению тока в катушке препятствует явление самоиндукции, поддерживающее ток в прежнем направлении. Этот убывающий от максимального значения I0 ток продолжает переносить заряды от одной обкладки
конденсатора к другой в том же направлении и перезаряжает конденсатор. Перезарядка заканчивается, когда ток становится равным нулю. В этот момент энергия магнитного поля катушки переходит в энергию электрического поля конденсатора. В следующий момент начинает разряжаться конденсатор, а ток потечёт в противоположном направлении. Ток разряда конденсатора возрастает пока конденсатор не разрядится полностью, а затем убывает, но вследствие явления самоиндукции снова перезаряжается

конденсатор и контур возвращается в исходное состояние. На этом завершается один период колебаний в контуре.
Взаимное превращение энергии электрического и магнитного полей сопровождается потерями (диссипацией) энергии на нагревание проводников. И если энергия не пополняется извне, то колебания в контуре затухают – амплитуда колеблющихся величин (заряд на обкладках конденсатора, напряжение, ток) каждого последующего цикла колебаний меньше предыдущего. Чем больше омическое сопротивление контура, тем быстрее затухают колебания в нём.
Закон затухания колебаний зависит от свойств колебательной системы.
Система называется линейной, если характеризующие данную систему в рассматриваемом процессе параметры не изменяются.
Линейные системы описываются линейными дифференциальными уравнениями. Электрический контур можно считать линейной системой, если его сопротивление R, электроёмкость C и индуктивность L не зависят ни от тока в контуре, ни от напряжения.
Найдём дифференциальное уравнение, описывающее свободные затухающие колебания линейной системы – электрического колебательного контура. Для этого воспользуемся законом Ома и вытекающим из него вторым правилом Кирхгофа, которые справедливы для цепей постоянного и квазипостоянного токов. В данном случае в цепи протекает переменный ток, но учитывая, что размеры контура l не слишком велики (т. е. l<c/ , где с – скорость света, с которой распространяются электромагнитные колебания; l – длина контура; – частота колебаний), то можно считать, что мгновенное значение тока будет практически одинаково во всех точках контура. Удовлетворяющие такому условию токи называются квазистационарными. Тогда согласно второму правилу Кирхгофа для RLC-контура, в котором протекают квазистационарные токи, можно записать
UR UC EL ,
(1)
где UR IR – падение |
|
напряжения |
|
на |
|
сопротивлении; |
|
UC |
q |
|
||||||||||||||||||||||||||||
C |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
– |
|
|
|
|
|
|
|
|
|
|
|
|
EL L |
|
dI |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
напряжение на конденсаторе; |
|
|
|
|
|
– ЭДС самоиндукции в ка- |
||||||||||||||||||||||||||||||||
|
|
|
dt |
|
||||||||||||||||||||||||||||||||||
|
|
тушке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Подставив эти значения в равенство (1), получим уравнение |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
IR |
q |
L |
dI |
|
IR+ |
q |
|
|
|
|
|
|
|
или |
|
|
|
L |
dI |
RI |
q |
0. |
(2) |
|||||||||||||
|
|
C |
dt |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
C |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
Учитывая, что I |
dq |
|
, и разделив (2) на L, |
получим |
|||||||||||||||||||||||||||||
|
|
|
|
|
dt |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
следующее уравнение |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
d2q |
|
|
|
R dq |
|
1 |
|
q 0. |
|
|
|
(3) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dt2 |
|
|
L dt |
LC |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Так как величина заряда на обкладках конденсатора пропорциональна разности потенциалов на них (q=CU), то уравнение, описывающее изменение напряжения на конденсаторе, будет аналогично предыдущему уравнению, т. е.
|
d2U |
|
R |
|
dU |
|
1 |
U 0. |
(4) |
|
|
dt2 |
|
|
|
||||||
|
|
L dt |
LC |
|
|
|||||
|
|
|
|
|||||||
Введя обозначения R2L, 1LC 02 , получим
|
d2U |
2 |
dU |
02U 0 |
, |
(5) |
|
|
dt2 |
|
|||||
|
|
dt |
|
|
|
||
где – коэффициент затухания; 02 – частота собственных незату-
хающих колебаний контура. Уравнение (5) является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и описывает свободные затухающие колебания.
При условии 0 решение уравнения (5) имеет вид
U(t) Um(t)cos( t ) U0e t cos( t ) |
, |
(6) |
|
|
|
где – начальная фаза; – частота свободных затухающих колеба-
ний; Um(t) – амплитуда затухающих колебаний.
|
|
|
|
1 |
|
R2 |
|
. |
|
|
||
|
02 2 |
(7) |
|
|||||||||
|
|
|||||||||||
LC |
4L2 |
|
||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
Um(t) U0e t |
, |
|
(8) |
|
||||||
|
|
|
|
|
||||||||
где U0 – значение напряжения при t 0. Амплитуда затухающих ко-
лебаний уменьшается с течением времени тем быстрее, чем больше коэффициент затухания . Для 0 график зави-
симости (6) изображен на рис. 2 сплошной линией, а зависимости (8) – пунктирной.
Затухающие U(t)
коле-бания не являются
периодиче- |
U0 |
|
t |
||||
Um (t) U |
0e |
||||||
скими, т. к. |
|
||||||
|
|
|
|||||
максималь- |
|
|
|
||||
ное значение |
|
|
|
||||
колеблю- |
|
|
|
||||
щейся |
вели- |
|
|
t |
|||
чины |
|
U1, |
|
|
|||
|
|
|
|
||||
|
|
|
|
|
|||
достигаемое |
|
|
|
|
|
||
в неко-торый |
|
|
|
||||
момент |
вре- |
T |
|
|
|||
мени t1, в по-
следующем
Рис. 2. Затухающие колеба-
при t t1 никогда не повторяется. Однако при затухающих
колебаниях какой-либо величины она обращается в нуль, достигает макси-мальных и минимальных значений через равные промежутки времени
T |
2 |
|
|
2 |
|
. |
(9) |
|
|
|
|
||||
|
|
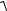 02 2
02 2
Величины T и называют условно периодом (условным
периодом) и циклической частотой (условной частотой) затухающих колебаний.
Промежуток времени , в течение которого амплитуда за-
тухающих колебаний уменьшается в e раз (e 2,718), на-
зывается временем релаксации. Введение понятия времени
