
1402
.pdfЕ.Ю. Руппель
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ
ПЕРЕМЕННОЙ
Омск●2008
3
Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия
(СибАДИ)
Е.Ю.Руппель
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
Учебное пособие
Омск Издательство СибАДИ
2008
4
УДК 517
ББК 22.1 Р 86
Рецензенты:
канд. физ.-мат. наук, доц. В.Г. Шантаренко (ОмГУПС);
канд. пед. наук, доц. Л.М. Нуриева (ОмГПУ)
Работа одобрена редакционноиздательским советом академии в качестве учебного пособия для специальностей направления «Эксплуатация транспорта и транспортного оборудования»
Руппель Е. Ю.
Р86 Интегральное исчисление функции одной действительной переменной:
Учебное пособие. – Омск: Изд-во СибАДИ , 2008. –89 с.
ISBN 978-5-93204-375-2
Учебное пособие предназначено для изучения студентами инженернотехнических специальностей дисциплины «Математика», охватывает такой раздел курса высшей математики, как интегральное исчисление функции одной переменной.
Содержание пособия соответствует государственному образовательному стандарту для студентов направления «Эксплуатация транспорта и транспортного оборудования». Пособие составлено таким образом, что наряду с теоретической частью содержит подробный разбор типовых задач, решение которых позволит студенту глубже понять и закрепить изученный материал. Каждый раздел содержит индивидуальные задания для самостоятельного решения.
Ил. 23. Библиогр.: 5 назв.
ISBN 978-5-93204-375-2 |
Е. Ю. Руппель, 2008 |
5

Учебное издание
Елена Юрьевна Руппель
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИОДНОЙ
ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ
***
Редактор И.Г.Кузнецова
***
Подписано к печати . . 2008 Формат 60 90 1/16. Бумага писчая Оперативный способ печати Гарнитура Times New Roman Усл. п. л. 5,5, уч.-изд. л. 5,5 Тираж экз. Заказ №
Цена договорная
Издательство СибАДИ 644099, г. Омск, ул. П. Некрасова, 10
Отпечатано в ПЦ издательства СибАДИ 644099, г. Омск, ул. П. Некрасова, 10
6
|
ОГЛАВЛЕНИЕ |
|
Глава 1. Неопределенный интеграл |
|
|
§1. Непосредственное интегрирование ………………………………… |
5 |
|
§2. Интегрирование подстановкой ……………………………………… |
7 |
|
§3. Интегрирование по частям ……………………………………….….. |
9 |
|
§4. Интегрирование простейших дробей …….......................................... |
11 |
|
§5. Интегрирование рациональных дробей……………………………... |
12 |
|
Схема интегрирования рациональных дробей………………..……. |
12 |
|
Случай, когда знаменатель разлагается лишь на неповторяющие- |
|
|
ся множители первой степени…………………………………….… |
14 |
|
Случай, когда знаменатель разлагается лишь на множители пер- |
|
|
вой степени, среди которых есть повторяющиеся…………………. |
15 |
|
Случай, когда знаменатель разлагается лишь на неповторяющие- |
|
|
ся множители второй степени и, возможно, множители первой |
|
|
степени…............................................................................................... |
16 |
|
§ 6. Интегрирование функций, рационально зависящих от тригоно- |
|
|
метрических функций |
|
17 |
§ 7. Некоторые интегралы тригонометрических функций...................... |
19 |
|
Интегрирование произведений синусов и косинусов....................... |
19 |
|
Вычисление интеграла sinm xcosnx dx, где m или n – положи- |
|
|
тельное нечетное целое число............................................................. |
|
19 |
Вычисление интеграла sinm xcosnx dx, где сумма m и n – отрица- |
|
|
тельное четное целое число................................................................. |
|
20 |
Вычисление интеграла sinmxcosn xdx m и n– четные неотрица- |
|
|
тельные числа........................................................................................ |
|
21 |
§ 8. Интегрирование некоторых алгебраических иррационально- |
|
|
стей......................................................................................................... |
|
22 |
Интегралы вида .......................R x,n x dx(n – натуральное число) |
22 |
|
Интегралы вида ....................................................... |
dx |
23 |
|
|
|
Задачи для индивидуальных ..................................................заданий |
24 |
|
Глава 2. Определенный интеграл..................................................................... |
|
39 |
§1. Определенный интеграл ......................и его геометрический смысл |
39 |
|
§2. Несобственные интегралы.................................................................... |
|
47 |
Интеграл с бесконечными .................................................пределами |
47 |
|
Интегралы от неограниченных ............................................функций |
48 |
|
Задачи для индивидуальных ..................................................заданий |
51 |
|
§3. Вычисление площадей ................................................плоских фигур |
60 |
|
Вычисление площади ......................в прямоугольных координатах |
60 |
|
Вычисление площади, ограниченной кривой, заданной парамет- |
58 |
|
рическими уравнениями....................................................................... |
|
62 |
Вычисление площади ................................в полярных координатах |
63 |
|
§ 4. Вычисление длины дуги …………………………………………..... |
64 |
|
7
Вычисление длины дуги кривой, заданной в прямоугольной сис- |
|
теме координат...................................................................................... |
65 |
Вычисление длины дуги кривой, заданной параметрическими |
|
уравнениями………………………………………………………….. |
67 |
Вычисление длины дуги кривой, заданной в полярных координа- |
|
тах........................................................................................................... |
68 |
§ 5. Вычисление объема.........................................................................…. |
71 |
Вычисление объема тела по известным площадям его попереч- |
|
ных сечений…………………………………………………............... |
71 |
Вычисление объема тела вращения.................................................... |
72 |
Задачи для индивидуальных заданий.................................................. |
75 |
Библиографический список…………………………………………. |
88 |
8
Глава 1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
§ 1. Непосредственное интегрирование
Многие физические и геометрические задачи сводятся к нахождению производных от функций. Наряду с этим ряд задач сводится к обратной операции – отысканию функции по ее производной. Эта операция называется интегрированием, следовательно, интегрирование должно заключаться в следующем: задана производная – требует-
ся найти функцию. |
|
|
Определение. Функцию y F x , |
заданную на промежутке x, |
|
называют первообразной для функции |
y f x , заданной на том же |
|
промежутке, если для всех x X выполняется равенство |
F x f x |
|
|
|
|
(или, что то же самое, равенство dF x f x dx). Например, для функ-
ции f x cosx первообразной будет |
функция F x sin x, т. к. |
|
|
x для всех x; |
для функции 3x2 первооб- |
F x sinx cosx f |
||
разной будет функция x3 |
|
для всех x; для скорости V |
, т.к. x3 3x2 |
||
точки первообразной будет путь S , который прошла эта точка, т. к. |
||
St V , и так далее.
Так как первообразная имеет производную, следовательно, она непрерывна. Но верно и более глубокое утверждение: если функция f x непрерывна, то она имеет первообразную. В интегральном исчислении мы будем иметь дело только с непрерывными функциями.
Если |
функция y F x |
является первообразной для функции |
y f x |
на промежутке X , |
то и любая из функций вида y F x C |
является первообразной для y f x на том же промежутке. Это сле-
дует из того, что
F x C F x C f x 0 f x .
Нетрудно убедиться в верности и обратного утверждения: если F x есть первообразная f x , то все первообразные для f x содержатся в формуле F x C.
Определение. Совокупность всех первообразных для заданной функции f x на промежутке x называется неопределенным инте-
гралом этой функции и обозначается так: f x dx (читается: ”инте-
9
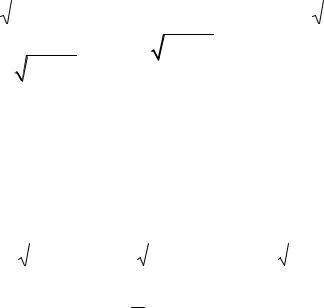
грал эф от икс дэ икс”);
f x называется подынтегральной функцией;
произведение f x dx– подынтегральным выражением;
знаком интеграла;
x– переменной интегрирования.
Если F x есть первообразная для f x , то f x dx F x C (C–
произвольная константа). Например, cosxdx sin x C;
3x2 dx x3 C.
Из определения интеграла следует, что каждой формуле дифференциального исчисления F x f x соответствует формула
f x dx F x dx С в интегральном исчислении, так что в частности
вся таблица производных может быть переписана в виде таблицы интегралов:
I. xndx |
xn 1 |
|
|
C, где n 1; |
|
|
|
II. |
dx |
|
ln |
|
x |
|
|
|
C; |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
III. axdx |
|
ax |
|
C; |
|
|
|
|
|
|
IV. ex dx ex C; |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ln a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
V. |
|
|
|
|
dx |
|
|
arcsin x C |
|
|
|
VI. |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
arcsin |
C; |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
1 x2 |
|
|
arccos x C |
|
|
|
|
|
|
|
|
|
|
a2 x2 |
|
|
|
|
|
|
|
|
a |
|||||||||||||||||||||||||||||||||||
VII. |
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
1 |
|
|
|
x a |
|
|
C; |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
ln |
|
x |
|
x2 a |
|
; VIII. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
|
|
|
2 |
|
2 a |
x a |
||||||||||||||||||||||||||||||||||||
|
x2 a |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
IX. cosxdx sinx C; |
|
|
|
X. sinxdx cosx C; |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
XI. |
|
dx |
ctg x C; |
|
|
|
XII. |
|
|
dx |
tg x C; |
|||||||||||||||||||||||||||||||||||||||||||||||||
sin2 x |
|
cos2 x |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
arctg x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
1 |
|
|
|
|
x |
C; |
|||||||||||||||||||||||||
XIII. |
|
|
|
|
|
; |
|
|
|
XIV. |
|
|
|
|
|
|
|
|
|
arctg |
||||||||||||||||||||||||||||||||||||||||
1 x2 |
|
|
a2 x2 |
|
|
a |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
arcctg x C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
)dx |
x |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
XV. ( |
|
|
x2 a |
|
x2 a |
|
ln |
x |
x2 |
|
a |
C; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
XVI. f ax b dx 1 F ax b . a
Займемся теперь основными свойствами неопределенных интегралов и правилами их вычисления.
Примем без доказательства свойства неопределенного интеграла:
10

1.f x dx f x ;
2.f x dx f x C;
3.d f x dx f x dx;
4.df x dx f x C ;
5.kf (x) dx k f (x) dx (k–постоянная);
6. f (x) g(x) dx f (x) dx g(x) dx .
§ 2.Интегрирование подстановкой
Замена переменной (подстановка) x t в интеграл производится по формуле
f x dx f t t dt ; |
(1.1) |
|
|
при этом говорят, что в интеграле слева сделана замена переменной (подстановка) x t . Формулой (1.1) можно пользоваться следующим образом: подобрать функцию x u t так, чтобы, подставив вместо x подынтегральное выражение, получить более простой интеграл.
Пример 1. Найти x
 x 3 dx.
x 3 dx.
Решение. С целью упрощения подынтегрального выражения по-
ложим |
|
|
x 3 t2 . |
|
|
|
|
|
|
|
Отсюда |
|
x t2 3; |
|
|
|
dx d t2 3 ; |
||||||||||||||||||
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
dx d t |
3 |
|
|
|
|
|
|
|
dx 2t 0 dt; |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt;dx (t |
|
|
|
|
|
|
dt; |
dx 2tdt . |
Заменив |
|||||||||||||||||||||||||
|
|
|
|
) |
|
3 |
|
||||||||||||||||||||||||||||
всюду под интегралом x на (t) t2 3, получим |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
x |
|
|
dx t2 3 |
|
|
|
2tdt 2t4 6t2 dt 2 t4dt 6 t2dt |
||||||||||||||||||||||||||||
|
|
|
|
t2 |
|||||||||||||||||||||||||||||||
x 3 |
|||||||||||||||||||||||||||||||||||
2 t4dt 6 t2dt 2 |
t4 1 |
|
6 |
t2 1 |
|
C |
2 |
t5 2t3 C |
2 |
|
|
|
5 |
||||||||||||||||||||||
|
|
x 3 |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 1 |
|
|
|||||||||||||||||||||||||||
2 |
|
|
|
3 C. |
|
|
4 1 |
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|||||||||||||||
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При вычислении воспользовались формулой xndx |
xn 1 |
|
C. |
||||||||||||||||||||||||||||||||
n 1 |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2xdx |
|
|
|
|
|
|
|
|
|
|||||||||||||
Пример 2. Найти |
|
|
|
|
3e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
e4x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Заметим, |
что e4x e2x 2 |
. Целесообразно ввести пере- |
|||||||||||||||||||||||||||||||||
11

менную e2x t . Тогда |
de2x dt ; |
|
e2x 2dx dt. Заменив |
e2x dx dt; |
всюду под интегралом e2xdх на |
dt |
, |
e2xна t, получим |
|
|
||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
3dt |
|
|
|
|
dt |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2x |
|
|
4x |
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ln |
|
t t |
|
5 |
|
C |
|
ln |
|
e |
|
|
e |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 t2 5 |
|
2 |
|
t2 5 2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Пример 3. Найти |
|
|
|
2sin xdx |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 cos2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. Заметим, что sin xdx d cosx, т.к. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ввести |
||||||
d cosx cosx |
dx sin xdx. Целесообразно |
||||||||||||||||||||||||||||||||
t cosx. Заменив всюду под интегралом sin xdx |
на dt |
||||||||||||||||||||||||||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5 C.
переменную
, cosx на t,
|
|
2sinxdx |
|
2 |
|
dt |
|
|
|
|
2ln |
t |
|
3 t2 |
|
C 2ln |
cosx |
3 cos2 x |
|
C. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
3 cos2 x |
3 t2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Пример 4. Найти sin 3x 1 dx. |
|
|
|
|||||||||||||||||||||||||||
|
|
Решение. Заметим, |
что |
dx |
1 |
d 3x 1 , т.к. |
d 3x 1 |
|||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||||||
|
|
Целесообразно ввести переменную t 3x 1. То- |
||||||||||||||||||||||||||||||
3x 1 dx 3dx. |
||||||||||||||||||||||||||||||||
гда dx |
1 |
dt. Заменив всюду под интегралом dx на |
1 |
dt, |
3x 1 на t; |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||||||||
получим |
1 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
sin 3x 1 dx |
|
|
|
|
cos 3x 1 C. |
|||||||||||||||||||||||||
|
|
|
|
|
sintdt |
|
|
cost |
|
|||||||||||||||||||||||
|
|
3 |
3 |
3 |
||||||||||||||||||||||||||||
|
|
На основании вышеизложенного можно ввести формулу |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
f ax b dx |
1 |
F ax b C , |
(1.2) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где F x – первообразная функции f x . |
|
|
|
|||||||||||||||||||||||||||||
|
|
Тогда e2x 3dx |
1 |
e2x 3 |
C. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Из формулы (1.2) получим
1. sin ax b dx 1 cos ax b C. a
2. cos ax b dx 1sin ax b C. a
12
