Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1402

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.12 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

то, приняв φ за параметр, найдем (рис. 15)

x r cos ;

y r sin ;

cos rsin ;

sin rcos ;

Формула (2.22) примет вид

dr 2

cos rsin

sin rcos d

d .

Окончательно имеем

dr 2

d .

(2.25)

Пример 4. Найти длину дуги гиперболической спирали rφ = 1 от точки А (2; 1/2) до точки В (1/2; 2) (рис. 16).

Решение. Разрешаем уравнение спирали относительно r: r 1 .

x		r r	B
	φ		φ =2
0	y		φ =1/2

Рис. 15

Рис. 16

При радиус-вектор спирали неограниченно уменьшается и витки спирали неограниченно приближаются к полюсу. Нас интересует длина дуги АВ спирали, соответствующая значениям полярного

угла

от

до

Из

уравнения

спирали

1 2

искомая

длина

находится по

формуле

(2.23):

			2				1				1 2				2						1							1					2		1				1
		l												d											1					d							1				d .
		l						2					2	d									2		1				2	d							1			2	d .
			1												1																		1
					2												2																	2
Введем замену переменной
																			1					1			z,
																			1					2			z,
																								2
тогда
																																1										1
	1			z2			1			z2 1;						1										z2 1						1						z2 1				1

1						;																									2		; d									2 dz
1		2				;		2																							2		; d									2 dz
		2						2								z		2	1
																z			1
	1									1	1									1									3									zdz
	1										1									1																		zdz
				z2		1			2			z2		1 dz								z2 1							2 2z dz
	2			z2		1			2			z2		1 dz						2		z2 1							2 2z dz										3
																																							3
																																				z2 1 2
																																				z2 1 2

zdz

z2 1 z2 1 .

Новые пределы интегрирования находим из соотношения

1	1	z; если	1	,	то zнижн		; если
						5
	2
		2

2, то zверхн 2 .

Таким образом,

5 5 5 5

	2																			zdz									2									z2dz											2					z2 1 1								2								1
	2																			zdz									2									z2dz											2					z2 1 1								2								1
l z z2 1																																																												dz				1								dz
																	z2 1																			z			2																z		2												z	2
																																							2																		2													2
																								z2 1																		1																1													1
						5																		z2 1										5								1									5							1					5								1
																																																																		5
			5									5
			5									5													5																					5																						1
		2								2															5											z 1										5
		2								2				1											2					1															2											5					1				2
dz														1				dz z							2					1		ln																								5			5		1	ln			2
														2																					z 1
														2
													z		1																		2																				2					2								5	1
			5									5														5																					5



																																																																2
	1			ln				5			1								5	1		ln					5	2										1			ln							5		1
	2			ln																		ln																			ln
	2							5 1									2 2										5 2						2															5 1
							1		ln							2							1														1			ln				3-
					5		1								5	2					5		1								5						1							3-								5

	2 2														5 2						5 1								2 2														3+ 5

				3-		2				3-

		1			5						5
	5	1	ln		5			5			5	.
									ln
				22			2		ln
2		2		22			2			2

§ 5. Вычисление объема

Вычисление объема тела по известным площадям его поперечных сечений

Пусть требуется вычислить объем V тела, заключенного между двумя перпендикулярами к оси 0х плоскостями х = а и х = b (рис. 17).

xi-1 ξi

Рис. 17

Предположим, что известна площадь любого сечения тела плоскостью, перпендикулярной к оси 0х. Эта площадь зависит от положения секущей плоскости, т. е. является функцией от х. Обозначим ее через S(x) и допустим, что она непрерывна на отрезке [а; b]. Разобьем отрезок [а; b] на n частей точками

а= х0 < х1 < х2 <... <хn-1 < хn = b

ичерез точки деления проведем плоскости, перпендикулярные к оси

0х.

Эти плоскости разобьют тело на n слоев. Обозначим через ∆Vi (i =1,2, ..., n) объем слоя, заключенного между плоскостями x = xi-1 и х =хi. Тогда ∆Vi приближенно равен объему цилиндра, высота которого равна ∆хi = хi – хi-1, а основание совпадает с поперечным сечением, образованным пересечением тела какой-либо плоскостью х = ξi, где хi-1≤ ξi ≤ хi, т. е. ∆Vi ≈ S (ξi) ∆хi, а объем всего тела

VS i xi .

По определению, принимаем

n	max xi ,
V lim S i xi	max xi ,
0i 1
т. е.
b
V S x dx.	(2.26)
a

Вычисление объема тела вращения

Пусть функция f(x), х [а; b], непрерывна на отрезке [а; b]. Требуется вычислить объем V тела, образованного вращением вокруг оси 0х фигуры, ограниченной линиями y =f (х); у = 0; х = а; х = b (рис. 18).

Так как любое поперечное сечение тела есть круг радиусом y , то площадь сечения будет S(x) = πy2 = πf 2(x).

Применив формулу (2.26), найдем

b	b
V y2dx f 2 x dx.		(2.27)
a	a

y					y	y2=4x
y		y=f(x)


0	a	x	b	x	0	4	x

Рис.18

Рис.19

Пример 1. Вычислить объем тела, образованного вращением вокруг оси 0х фигуры, ограниченной линиями y2 = 4х; у = 0; х = 0; х = 4 (рис. 19).

Решение. Такое тело называется параболоидом вращения. Применив формулу (2.27), получим

2 42 2 02 32 .

V 4хdx 4

Пример 2. Вычислить объем тела, образованного вращением эл-

липса

х2

1 вокруг оси 0х (рис. 20).

Решение. Рассматриваемое те-

ло называется

эллипсоидом вра-

щения. Эллипс пересекает ось 0х в

точках х = – а и х = а.

Из уравнения эллипса находим

a2 x2

-a

a x

Ввиду симметричности эллип-

са относительно оси 0у вычислим

-b

объем в пределах от 0 до а и полу-

ченный результат удвоим:

Рис. 20

V 2

a2 x2 dx 2

a2dx

0 a

2 a

2 b2 x

2dx 2 b2 dx 2 b

2 x2dx 2 b2x

0 2 b2

0 a

2 b

a 2

2 b2a3

2 b2

4 ab2

3a2

Пример 3. Вычислить объем тела, образованного вращением вокруг оси 0х; фигуры, ограниченной линиями y = 2 и y =x2 + 1 (рис. 21).

Решение. Решая систему

y 2;	y 2;	y 2;

y x2 1,	x2 1,	x 1,

находим точки пересечения данных линий: А (–1; 2) и B(1;2). Ввиду симметричности вращающейся фигуры вычислим объем в пределах от 0 до 1 и результат удвоим.

Из рис. 21 видно, что искомый объем равен разности объемов тел, образованных при вращении вокруг оси 0х фигур A1ABB2 и A1ACBB1. Таким образом,

1			1						1		1				1				1
V 2 22dx 2 x2 12dx 8 dx 2 x4 2x2 1dx 8 dx 2 x4dx
0			0			1			0		0				0				0
1		1						x5		1		x3	1	10			15		13
1		1								1			1
4 x2dx 2 dx 8 x							2				4		2 x		8 2			4		2


							5				3				5				3
0		0				0	5			0	3		0		5				3
0		0				0				0			0
6	2	4	64	.
6		3	15	.
5		3	15
		y	y = 2													y
			y = 2													y

	A				B											d
						y = x2 + 1
	A1			B1				x								c			x = φ(y)
-1			1					x								c
															0					x

Рис. 21

Рис. 22

Аналогично доказывается, что объем тела, образованного вращением вокруг оси 0у фигуры, ограниченной линиями x = φ(y); х = 0; у = с; y = d (pиc. 22), вычисляется по формуле

	d		d
	V x2dy 2 y dy.					(2.28)
	c		c
	y			Пример 4. Вычис-
				Пример 4. Вычис-
	B			лить объем тела, обра-
	B		A	зованного	вращением
	1			вокруг оси 0у фигуры,
				вокруг оси 0у фигуры,
			y = x2	ограниченной		линиями
			y = x2	y = x2 и у = х (рис. 23).
				Решение.		Решая
-1	0	1	x	систему
-1	0	1	x	y x2;	x x2;
	Рис. 23
	Рис. 23			y x,	y x,

x x2 0;	x 1;	x 0;

y x,	y 1,	y 0,

находим точки пересечения заданных линий: 0(0;0) и А(1;1). На рис. 23 видно, что искомый объем равен разности объемов тел, образованных вращением вокруг оси 0у криволинейной трапеции 0mАВ и треугольника 0АВ. Объемы этих тел находим по формуле (2.28), причем в качестве подынтегральных функций следует взять соответст-

венно х = у и x y 2 . Пределами интегрирования являются ординаты точек 0 и A, т. е. с = 0 и d = l. Таким образом,


1	1	1	1			1	1		y2	1	3				1	y2	1			3	12


			y		2							y		2				2
V y2dy ydy																			12

			1
0		0		1				2		0			3		2		0	3			2
			2								2

							0								0

2 .

3 2 6

Задачи для индивидуальных заданий

Вариант 1

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

4y 8x x2; 4y x 6.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x3t2;y 3t t3 0 t 2 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

rcos ; r cos2 .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

y 2lnsin0,5x.

Вариант 2

1. Вычислить площадь фигуры ограниченной графиками функ-

ций

y9 x2; y x2 1.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

xcost; y sint 0 x 2 2 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

rcos2 .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

	2	3
y		3 x		1 x 3 .
			2

3

Вариант 3

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x2 1; x y 3.

2. Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

y1 cost; x t sint 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

rsin ; r 2sin .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

yarcsinx 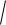1 x2 0 x 15 .

Вариант 4

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x; x 4;y 1x2 .

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x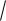2cost; y 4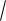2sint 0 x 1 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r2,5sin ; r 1,5sin 0 4 .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

				9
y arccosx	1 x	2	0 x
					.
				16

Вариант 5

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y2x2; y 2x2; x 2.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

y3 1 cost ; x 3 t sint 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r cos ; r

	2cos			.

		4	4

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

				8
y arccosx	1 x	2	0 x
					.
				9

Вариант 6

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y2 2x 1; x y 1 0; x 0.

2.Вычислить площадь области, ограниченной кривой, заданной в параметрической системе координат

x2cost cos2t; y 2sint sin2t 0 t .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r 6sin3 .

4. Вычислить длину кривой, заданной уравнением в декартовой системе координат

				1
			2
			2
y 2 arcsin	x	x x				x 1 .
y 2 arcsin	x	x x			4	x 1 .
					4

Вариант 7

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

y x2 2x; x y 4 0.

2.Вычислить площадь фигуры, ограниченной петлей линии

x3t2; y 3t2 t4 .

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r2,5cos ; r 1,5cos 0 4 .

4.Вычислить длину кривой, заданной уравнением в декартовой системе координат

yln 1 x2 0 x 1 .

Вариант 8

1. Вычислить площадь фигуры, ограниченной графиками функ-

ций

yex; x y 1; x 4.

2.Вычислить площадь фигуры, ограниченной петлей линии

xt2 1; y t3 t.

3.Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах

r sin3 .

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.11 Mб11399.pdf
#
07.01.2021193.56 Кб014.pdf
#
07.01.2021309.74 Кб0140.pdf
#
07.01.20211.12 Mб01400.pdf
#
07.01.20211.12 Mб01401.pdf
#
07.01.20211.12 Mб111402.pdf
#
07.01.20211.12 Mб01403.pdf
#
07.01.20211.12 Mб161404.pdf
#
07.01.20211.12 Mб31405.pdf
#
07.01.20211.12 Mб121406.pdf
#
07.01.20211.12 Mб21407.pdf