
- •Введение
- •5.1. Метод Эйлера (Метод Рунге-Кутта 1-го порядка)
- •5.3. Метод Рунге-Кутта 3 порядка
- •5.4. Метод Рунге-Кутта 4-го порядка
- •7.1. Методы одномерной оптимизации
- •7.3. Метод локализации экстремума
- •7.4. Метод золотого сечения
- •7.5. Метод Фибоначчи
- •8. МЕТОДЫ МНОГОМЕРНОЙ ОПТИМИЗАЦИИ
- •8.1. Метод градиента
- •Лабораторная работа № 1
- •Лабораторная работа № 2
- •Лабораторная работа № 3
- •Лабораторная работа № 4
- •Лабораторная работа № 5
- •Лабораторная работа № 6
- •Лабораторная работа № 7
- •Лабораторная работа № 8
- •Лабораторная работа № 9
- •Библиографический список

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Сибирская государственная автомобильно-дорожная академия (СибАДИ)»
Кафедра "Информационные технологии"
АВТОМАТИЗИРОВАННОЕ ПРОЕКТИРОВАНИЕ
СибАДИУчебно-методическое пособие
Составили: А.А. Соловьев, Ю.И. Привалова
Омск 2016
УДК 681.5 ББК 32.965 А22
Рецензенты:
канд. техн. наук, доц. И.М. Князев (СибАДИ); канд. физ.-мат. наук, доц. В.В. Лизунов (Сибирское отделение академии военных наук РФ)
Автоматизированное проектирование [Электронный ресурс] : учебно-методическое пособие / сост. : А.А. Соловьев, Ю.И.
А22 Привалова. – Электрон. дан. – Омск : СибАДИ, 2016. – URL: http://bek.sibadi.org/cgi-bin/irbis64r_plus/cgiirbis_64_ft.exe. - Режим доступа: для авторизованных пользователей.
ISBN 978-5-93204-936-5.
Содержит теорию, задания к лабораторным работам, контрольные вопросы. Имеет интерактивные оглавление и элементы на первом титульном экране.
Предназначено для аспирантов направления подготовки «Наземные транспортно-технологические комплексы».
Работа утверждена редакционно-издательскимСибАДИсоветом СибАДИ в качестве учебно-методического пособия.
Текстовое (с мвольное) издание (862 КБ).
Систем. требования: Intel, 3,4 GHz; 150 Мб; Windows XP/Vista/7; DVD-ROM;
1 Гб свободного места на жестком диске; программа для чтения pdf-файлов Adobe Acrobat Reader, Google Chrome
Издание первое, комплексного распространения Дата подписания к использованию 14.06.2016
Издательско-полиграфический центр СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПЦ СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1
ФГБОУ ВО «СибАДИ», 2016

Введение
Проектированием называют деятельность по созданию проекта. Понятие «проект» до недавнего времени обозначало технический проект (design) − представление в некоторой принятой форме прототипа или прообраза проектируемого технического объекта, системы или процесса, а также комплект документации, предназначенной для создания объекта, его эксплуатации, ремонта и ликвидации. В настоящее время в связи с широким внедрением информационных технологий во все области деятельности человека, например, в биологию и медицину, понятие проекта существенно расширено. Приведенное определение проекта следует отличать от понятия проекта (project), используемого при планировании, организации и управлении ресурсами для достижения определенных целей [1].
Проектирование начинается с разработки технического предложения и
вания. Обязательным документом технического задания на техническое из-
(или) технического задания и представления их в виде проектной документации, необходимой и достаточной для последующейИматериальной реали-
зации объекта проектирования в виде изделия, системы или процесса. Техническое задание – это исходное (первичноеД) описание объекта проектиро-
делие является спецификация – конструкторскийА документ, определяющий
состав этого изделия. В спецификации содержится подробное перечисление
деталей и узлов, входящих вбсостав изделия [1].
Результатом проектирования, как правило, является полный комплект документации, представляющийисо ой окончательное описание объекта или
процесса и содержащ й достаточные сведения для реализации объекта или процесса на данном предпр ят . Можно сказать, что проектирование – это процесс полученияСи преобразования исходного описания объекта или процесса в окончательное описание на основе выполнения комплекса работ исследовательского, расчетного и конструкторского характера. Проектирование, при котором все проектные решения или их часть получают путем взаимодействия человека и ЭВМ, называют автоматизированным, в отличие от «ручного» (без использования ЭВМ) или автоматического (без участия человека). Автоматическое проектирование в настоящее время возможно лишь в отдельных, хотя, быть может, очень важных частных случаях (например, в микроэлектронике) [1].
3

1.СИСТЕМЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ
Комплекс программно-технических средств вычислительной техники, необходимых и достаточных для проектирования конкретного изделия, называют системой автоматизированного проектирования (САПР). Часто название «САПР» включает в себя предметную область, на которую ориентирована эта система. Так, различают системы ECAD (Electronic Computer Aided Design) для проектных работ в электронике, микроэлектронике и вычислительной технике; MCAD (Mechanical CAD) –ориентированные на машиностроительные отрасли и др. [1].Выделяют следующие стадии проектирования:
1стадия. Научно-исследовательские работы (НИР). Выполняется в научно-исследовательских институтах (НИИ)И. На этой стадии изучаются существующие прототипы будущего изделия, патенты, лицензии и прини-
маются принципиальные решения о технических параметрах будущего изделия. На завершении научно-исследовательскихДработ разрабатывается на- учно-исследовательский отчет, который содержит техническое задание и технические предложения. Для автоматизацииА на этой стадии используются автоматизированные системы научных исследований (АСНИ).
2стадия. Опытно-конструкторскиеб работы (ОКР). Выполняется в конструкторских бюро (КБ). На этой стадии выполняется детальная проработка проекта, ориентированнаяина конкретные заводы-изготовители. По завершении опытно-конструкторских работ формируется комплект конструкторской документацС. Для автоматизации используются системы автоматизированного проект рован я (САПР).
3стадия. Производство образца. Выполняется на заводахизготовителях. На этой стадии разрабатывается технологический процесс изготовления всех деталей изделия, сборка в конечное изделие и производство опытного образца. Для автоматизации используются автоматизированные системы управления технологическими процессами (АСУТП), автоматизированные системы управления производством (АСУПр), автоматизированные системы управления предприятием (АСУП).
4стадия. Опытное испытание. Выполняется на специализированных полигонах. На этой стадии происходит обработка и анализ данных об испытании и составляется акт о запуске в серийное производство.
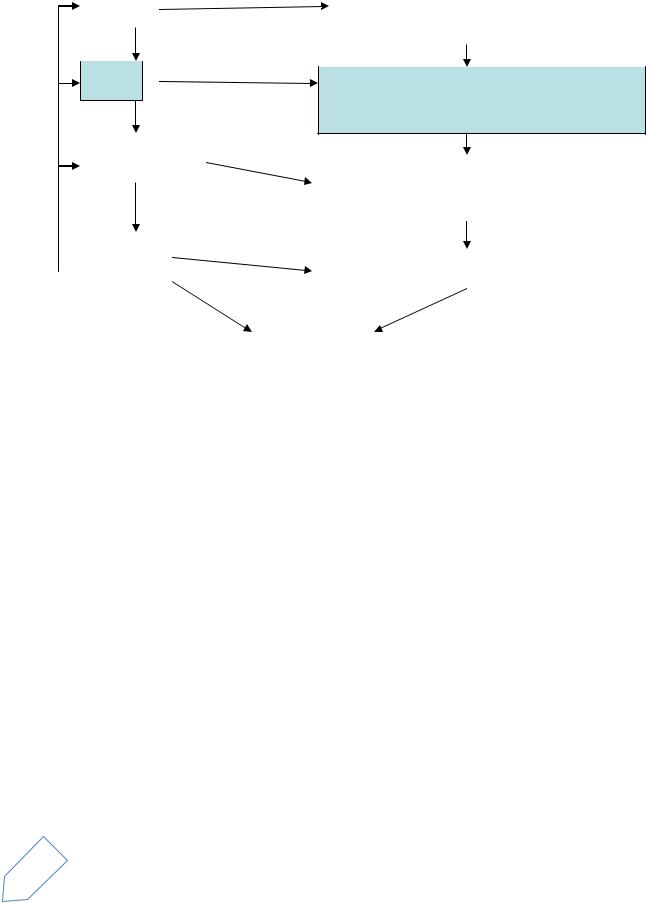
При переходе от одной стадии к другой степень детальности проработки проекта возрастает, так что рабочий проект должен быть достаточным для изготовления опытных или серийных образцов [1]. Стадии процесса проектирования разбивают на этапы, которые более детально характеризуют разработку проектируемого объекта (рис. 1).
4
Стадии проектирования |
|
Этапы проектирования |
|
|
|
|
|
|
|
1. |
Согласование технического задания |
|
1. |
НИР |
|
|
|||
|
|
2. |
Формирование технических предложений |
|||
|
|
|
|
|||
|
|
|
|
3.Инженерный анализ и оптимизация |
||
|
|
|
|
|||
|
|
|
|
|
||
2. |
ОКР |
|
|
|
|
|
4. Эскизное проектирование |
||||||
5.Техническое проектирование
6.Разработка конструкторской документации
|
3. Производство |
|
|
|
|
|
|
|
|
|
|
образца |
|
|
7. |
Технологическое проектирование |
|
||||
|
|
|
|
|
8. |
Разработка технологической документации |
|
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
9. |
|
|
|
И |
|
|
|
|
|
|
Изготовление опытного образца |
|
||||
|
4. Опытное |
|
|
|
|
Д |
|
|||
|
испытание |
|
|
|
10. Испытание |
|
|
|||
|
|
|
11. Отработка конструкторской документации |
|
||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
Серийное производство |
|
|
|
|||
|
|
|
|
б |
|
|
|
|
||
|
|
|
|
Рис. 1. Стадии и этапы проектирования |
|
|||||
Этапы разделяютина составные части, называемые проектными процедурами. ПримерамиСпроектных процедур являются подготовка чертежей, анализ кинематики издел я ли его части, моделирование переходных процессов, оптимизация параметров и структур. Таким образом, процесс проектирования представляет собой выполнение некоторых последовательностей типовых проектных процедур.
Основными направлениями типовых процедур проектирования являются:
1.Расчет (Одновариантный анализ). Определение выходных параметров и характеристик объекта проектирования при неизменных значениях его внутренних параметров и постоянной структуре.
2.Анализ (Многовариантный анализ). Определение изменения выходных параметров и характеристик объекта в зависимости от изменения его внутренних параметров.
3.Оптимизация. Определение наилучших (оптимальных) значений выходных параметров и характеристик путем целенаправленного изменения внутренних параметров объекта (параметрическая оптимизация) или его структуры (структурная оптимизация).
5

4. Синтез. Генерация исходного варианта проектируемого объекта, включая его структуру (структурный синтез) и значение внутренних параметров (параметрический синтез).
Для решения основных типовых процедур наибольшее распространение получили системы автоматизированного проектирования (САПР). Структура САПР состоит из подсистем. Подсистема САПР – это выделенная по некоторым признакам часть САПР, обеспечивающая выполнение определенных проектных задач. Различают подсистемы проектирующие и обслуживающие. Проектирующие подсистемы выполняют непосредственно проектные процедуры. Примерами таких подсистем могут служить подсистемы геометрического трехмерного моделирования механических объектов
иподготовки конструкторской документации. Обслуживающие подсистемы обеспечивают функционирование проектирующих подсистем. Типичными
обслуживающими подсистемами являются подсистемы управления проектными данными, подсистемы разработки и сопровожденияИ программного обеспечения CASE (Computer Aided Software Engineering), обучающие под-
системы для освоения пользователями технологийД, реализованных в САПР
идр. [1]. А
средство обеспечения САПРб. Основные виды обеспечения САПР следующие: и
Техническое обеспечен е САПР. (ТО САПР) – совокупность связан-
ных и взаимодействующСх техн ческих средств (ЭВМ, периферийные устройства, сетевое оборудован е, л нии связи и др.).
Математическое обеспечение САПР. (МО САПР) – совокупность математических методов, моделей и алгоритмов, используемая для решения задач автоматизированного проектирования.
Программное обеспечение САПР. (ПО САПР) – совокупность про-
грамм, необходимая для функционирования САПР.
Информационное обеспечение САПР. (ИО САПР) – совокупность программно-технических средств, предназначенная для ввода, хранения, преобразования и вывода графической и текстовой информации.
Лингвистическое обеспечение САПР (ЛО САПР) – совокупность языков, используемая САПР для представления информации о проектируемых объектах, для обмена данными между техническими средствами, а также для осуществления диалога между проектировщиком и ЭВМ.
Методическое обеспечение САПР. (Мет САПР) – описание техноло-
гии функционирования САПР, методов выбора и применения пользователями технологических приемов для решения.
6
Правовое обеспечение САПР. (ПрО САПР) – совокупность правовых норм, регламентирующая правоотношения при функционировании САПР и юридический статус результатов её использования (функционирования).
Основная цель создания САПР − повышение эффективности труда инженеров. Под этим понимается:
− сокращение трудоёмкости проектирования и планирования; − сокращение сроков проектирования; − сокращение себестоимости проектирования и изготовления; − уменьшение затрат на эксплуатацию;
− повышение качества и технико-экономического уровня результатов проектирования;
− сокращение затрат на натурное моделирование и испытания. Достижение данных целей обеспечивается за счет:
− автоматизации оформления документации; − информационной поддержки и автоматизации принятия решений;
− унификации проектных решений и процессов проектирования; |
||
− повторного использования проектных решений, данных и наработок; |
||
− стратегического проектирования; |
|
|
− замены натурных испытаний и макетирования математическим мо- |
||
делированием; |
|
И |
|
|
|
− повышения качества управления проектированием. |
||
В настоящее время используетсяДнесколько видов классификации |
||
|
А |
|
1.По отраслевомуиназначению САПР можно классифицировать
следующим образом:
− машиностроСтельные САПР (MCAD mechanical computer-aided design) (разработка ш рочайшего спектра изделий: от создания аэрокосмических систем до проектирования кофеварок и кухонных комбайнов);
− EDA electronic design automation или ECAD electronic computer-aided design (САПР электронных устройств, проектирование печатных плат, радиоэлектронных средств);
− AEC CAD (architecture, engineering and construction computer-aided design) или CAAD (computer-aided architectural design) (САПР в области ар-
хитектуры и строительства, используется для проектирования зданий, промышленных объектов, дорог, мостов и пр).
2.По целевому назначению САПР можно классифицировать следующим образом:
− CAD (computer-aided design) (конструкторские САПР, для создания конструкторской и технологической документации, проектирования и создания чертежей ( например, программа AutoCAD и др.)).
− CAE (computer-aided engineering) (САПР функционального проекти-
рования, для автоматизации инженерных расчетов, анализа и симуляцииСАПР: б
7
физических процессов, осуществляют динамическое моделирование, проверку изделия).
−CAM (computer-aided manufacturing) (технологические САПР, для технологической подготовки производства (АСТПП)).
3. Классификация САПР по масштабу:
−отдельные программно-методические комплексы (ПМК) САПР (например, комплекс анализа прочности механических изделий в соответствии
сметодом конечных элементов (МКЭ) или комплекс анализа электронных схем);
−системы ПМК;
−системы с уникальными архитектурами не только программного (software), но и технического (hardware) обеспечений.
Многие САПР совмещают в себе решение задач, относящихся к раз-
ным аспектам проектирования CAD/CAM, CAD/CAE, CAD/CAE/CAM. Та-
кие системы называют комплексными или Иинтегрированными. Область применения САПР очень велика. Возможности САПР во многом определяются программным обеспечением, котороеДзачастую делят на уровни, опираясь на сложность системы и область ее возможностей.
Системы автоматизированного проектирования нижнего уровня в основном применяются при выпускеАконструкторской документации, обычно они не связаны друг с другом, а также С ПР, которые обеспечивают выпуск комплектов конструкторскойбдокументации (КД). Применяются такие системы в создании проектов с различной степенью сложности в области строительства, архитектурыи, геодезии, генплана, машиностроения и других.
САПР среднего уровня о еспечивает моделирование в трехмерном пространстве, а такжеСвыпуск документации на проектируемые модели. Об-документирования и проектирования изделий.
САПР верхнего уровня позволяет производить комплексное решение задач в моделировании объектов, выпуска конструкторской документации, расчетов, помогает решить специфические прикладные задачи. Например, моделирование самолетов, испытание двигателей, ядерных реакторов.
8

2.МАТЕМАТИЧЕСКИЕ МОДЕЛИ И ЧИСЛЕННЫЕ МЕТОДЫ В СТРУКТУРЕ МАТЕМАТИЧЕСКОГО ОБЕСПЕЧЕНИЯ САПР
Среди всех видов обеспечения современных систем автоматизированного проектирования особое место занимает математическое обеспечение, которое отличается разнообразием используемых методов вычислительной математики, статистики, математического программирования, дискретной математики и искусственного интеллекта, способных решать проектные процедуры синтеза или анализа любой сложности.
Математические модели, численные методы и соответствующие алгоритмы, используемые в системах автоматизированного проектирования, относятся к математическому обеспечению САПР. САЕ-системы машино-
•выполнение инженерных расчетов с цельюИопределения исходных параметров и данных для последующегоДматематического моделирования проектируемых объектов;
•математическое моделированиеАпроектируемых объектов, инженерный анализ и оптимизация проектных решений при изменении параметров
этих объектов.
Процесс математическогобмоделирования технических изделий и объектов в общем случае можно представить как последовательность следующих четырех основныхиэтапов [1]:
1) получение на основе фундаментальных физических законов исходной математическойСмодели объекта исследования в форме систем уравнений, математических выражен й, зависимостей и т.п.;
2) выбор численных методов и алгоритмов решения уравнений математической модели;
3) выбор или разработка на выбранном алгоритмическом языке и отладка программы, реализующей указанные методы и алгоритмы;
4) ввод исходных данных для выбранной или разработанной програм- мы-решателя исходных данных, получение и обработка результатов математического моделирования на ЭВМ.
В машиностроительных САЕ-системах используют математические модели объектов проектирования двух основных типов:
− модели объектов с сосредоточенными параметрами; − модели с распределенными параметрами.
Математическая модель, как правило, приближенно описывает иссле-
дуемый объект. Поэтому она должна соответствовать основным требованиям адекватности, точности и экономичности. Модель называют адекватной,строительных изделий призваны решать две следующие основные задачи
9
если она отражает свойства объекта с заданной точностью. Под точностью понимают степень соответствия оценок одноименных свойств объекта и его модели. Экономичность модели определяется затратами машинного времени и памяти, требуемыми для реализации на ЭВМ.
Адекватность модели оценивают перечнем отражаемых свойств объекта и областью адекватности. Областью адекватности называется область в пространстве параметров объекта, в пределах которой погрешности (точность) модели находятся в допустимых для пользователя пределах. Пусть, например, P=(p1,p2,...,pn) − вектор рассматриваемых параметров модели объекта проектирования и ε1,ε2,…,εn предельно допустимые значения относительной точности этих параметров. Тогда область адекватности Ар представляет собой множество всех тех значений параметров p1,p2,...,pn, для которых их относительная погрешность не превышает предельно допусти-
мой [1]. |
И |
При моделировании объектов с сосредоточенными параметрами ма- |
|
тематическая модель представляет собой систему обыкновенных диффе-
ренциальных и (или) алгебраических уравнений. |
спользуют три следую- |
|||||||||||||||||||
щие основные модели объектов с сосредоточенными параметрами [1]. |
||||||||||||||||||||
1. Модель в форме задачи Коши (явная форма) определяет система |
||||||||||||||||||||
обыкновенных дифференциальных уравнений (О |
|
У) вида |
||||||||||||||||||
|
|
|
|
б |
Д |
0 |
|
|||||||||||||
|
|
|
f1(x1,x2,...,xn,t), x1(0) |
|
, |
|||||||||||||||
|
x1 |
x1 |
||||||||||||||||||
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
f |
|
(x ,xА,...,x ,t), x |
|
(0) |
x |
0, |
||||||||||||
|
x |
|
|
|
||||||||||||||||
|
|
|
2 |
|
2 |
|
1 |
2 |
|
|
n |
|
|
2 |
|
|
|
2 |
||
|
.... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
(t) f |
|
(x ,x |
|
,...,x |
|
,t), |
x |
|
(0) x0, |
|||||||||
|
x |
n |
n |
2 |
n |
n |
||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
n |
|||||
где x1 ,x2 ,...,xn − |
фазовые переменные (они же переменные состояния), |
|||||||||||||||||||
С0 0 |
0 |
− |
|
известные начальные условия; [0,tK ] − рас- |
||||||||||||||||
t [0,tK ] − время; |
x1 ,x2 |
,...,xn |
|
|||||||||||||||||
сматриваемый интервал времени. В более лаконичной векторной форме система ОДУ записывается в виде
X F(X,t), X(0) X 0 , t [0,tK ],
где X − (n 1) − вектор фазовых переменных с компонентами x1 ,x2 ,...,xn ; F(X, t) − вектор-функция той же размерности; Х0 − аналогичный вектор начальных условий.
10

2. Модель в дифференциально-алгебраической форме (полуявная фор-
ма) имеет вид
|
|
X(0) X |
0 |
, t [0,t |
|
], |
X F(X,t), |
|
|
||||
|
|
|
|
|
K |
|
G(X,Y) 0,
где Y (y1 , y2 ,..., ym )− (m 1) − вектор алгебраических переменных, G(X,Y)− (m 1) − вектор-функция.
3. Модель в дифференциально-алгебраической форме (неявная форма)
определяет система уравнений
G(X, X,Y,t) 0, X(0) X 0, Y(0) Y0, t [0,tK ],
ния, описывающие состояния элементов объектаИ, называют компонентными уравнениями, а уравнения, задающиеАвзаимосвязи элементов объекта, —
где G − ((n m) 1) − вектор-функция.
Рассмотренные математические модели вида строят на основе компонентных и топологических уравненийДобъекта проектирования. Уравне-
топологическими. Таким образом, математическая модель объекта с сосредоточенными параметрами представляетб собой совокупность компонентных и топологических уравнений этого о ъекта [1, 2].
Математическимиимоделями о ъектов с распределенными параметрами, используемыми в САПР, являются в основном краевые задачи для дифференциальныхСуравнен й в частных производных (ДУЧП). Фазовыми переменными в эт х уравнениях могут быть температура (если речь идет о задаче теплопроводности, например), величина механического напряжения (в задаче анализа на прочность) и т.д. Различают стационарные и нестационарные краевые задачи для ДУЧП. В стационарной краевой задаче решение не зависит от времени. В качестве независимых переменных в такой задаче чаще всего используют пространственные переменные x, у, z. В нестационарной краевой задаче решение меняется во времени. В качестве независимых переменных в данном случае используются пространственные переменные x, у, z и время t [1, 2].
Как в стационарной, так и в нестационарной краевых задачах для ДУЧП должны быть заданы граничные условия — значения фазовых переменных и (или) их некоторых функций на границе моделируемого объекта. Различают граничные условия первого, второго и третьего рода [1, 2].
Граничные условия первого рода {условия Дирихле) − это значения фа-
зовых переменных V, заданных на границе области V(Г) = VГ.
Граничные условия второго рода (условия Неймана) имеют вид
11

dV
k dn |Г q,
где к и q — как правило, константы; я — нормаль к поверхности объекта.
Граничные условия третьего рода представляют собой так называе-
мые уравнения баланса вида |
dV |
|
0. |
|
f |
|
,V |
||
|
||||
|
dn |
|
|
|
В нестационарных задачах, кроме краевых условий, должны быть заданы начальные условия — значения фазовых переменных и (или) их некоторых функций внутри объекта в начальный момент времени:
V(0) =V0.
Компонентные и топологические уравнения объектов различной фи-
хом могут быть использованы при математическомИмоделировании не только механических, но и электрических, гидравлических, пневматических и
зической природы отражают различные физические законы, но могут иметь
одинаковый формальный вид, т.е. быть аналогичными. Наличие таких ана-
логий приводит к тому, что многие компонентные и топологические урав-
нения оказываются инвариантными к предметной области и с равным успе-
тепловых объектов. Указанное единство математических моделей особенно |
|||||
|
|
|
|
Д |
|
удобно при анализе объектов, состоящих из физических разнородных эле- |
|||||
ментов. |
|
|
|
|
|
Компонентное уравнен е i-гоАэлемента исследуемого объекта имеет |
|||||
общий вид [1, 2] |
б |
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
|
Fi (Vi,Vi,t) 0, |
|
||
где Vi − |
|
и |
|
|
− вектор- |
вектор фазовых переменных данного элемента; Fi |
|||||
функция соответствующейСразмерности.
Топологическое уравнение объекта можно представить в виде
T(V) 0,
где V {Vi} − вектор фазовых переменных объекта; Т − вектор-функция. Различают фазовые переменные двух типов − фазовые переменные
типа потенциала (например, электрическое напряжение, скорость в механической поступательной системе) и типа потока (например, электрический ток, сила, действующая на тело, в механической системе). Каждое из компонентных уравнений описывает связи между разнотипными фазовыми переменными, относящимися к данному компоненту. Например, второй закон
12

Ньютона описывает связь между силами, действующими на тело, и приобретаемым им ускорением [1,2].
Топологическое уравнение определяет связи между однотипными фазовыми переменными в разных элементах объекта. Например, принцип Даламбера для механической поступательной системы требует, чтобы сумма всех сил, действующих на тело с учетом инерциальных сил, была равна ну-
лю [1, 2].
Математические модели объектов с сосредоточенными параметрами удобно представлять в графической форме в форме эквивалентных схем, которые часто используются в качестве входного языка в САЕ-системах. Совокупность компонентных и топологических уравнений представляет собой математическую модель объекта проектирования в форме системы обыкновенных дифференциальных уравнений (ОДУ). В явном виде матема-
тическая модель объекта проектирования в форме системы ОДУ и (или) системы линейных, нелинейных алгебраических уравнений может быть решена с использованием численных методов решения систем линейных, нелинейных, дифференциальных уравнений, а также с помощью методов оптимизации.
|
|
|
|
И |
|
|
|
Д |
|
|
|
А |
|
|
|
б |
|
|
|
и |
|
|
|
|
С |
|
|
|
|
13

3.ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Математическое моделирование технических устройств, объектов и систем часто приводит к решению систем линейных уравнений. Для автоматизации их решения используют численные методы.
Рассмотрим систему линейных уравнений (СЛУ) с n неизвестными:
a11 |
|
x1 |
|
|
a12 |
|
x 2 |
|
|
... |
a1 n x n |
|
|
b1 ; |
||||||||
a 21 |
|
x1 |
|
a 22 |
x 2 |
|
|
|
... |
a 2 n x n |
|
|
b 2 ; |
|||||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a n 1 x1 |
|
a n 2 x 2 |
|
|
|
... |
a nn |
x n |
|
|
b n . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||
В матричной форме записи система имеет вид |
|
|
||||||||||||||||||||
A X B, |
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|||||||
где n – порядок системы; |
|
|
|
|
|
|
|
|
||||||||||||||
|
a |
|
|
a |
... |
|
a |
|
|
|
|
|
|
|||||||||
|
|
11 |
|
|
12 |
|
|
|
1n |
|
|
|
|
|
|
|||||||
|
a21 |
|
a22 |
... |
|
|
|
|
б |
|
|
|
||||||||||
A |
|
|
|
|
|
|
|
|
|
|
|
|
– матрица коэффициентов системы; |
|||||||||
|
... |
|
|
|
|
и |
А |
|
|
|
|
|
||||||||||
|
a |
n1 |
|
a |
n2 |
... |
|
a |
nn |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
B |
b2 |
– вектор свободных членов; |
X |
x2 |
– вектор неизвестных. |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
... |
|
|
|
С |
|
|
|
|
|
|
... |
|
|
||||||||
|
b |
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
|||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В свернутой форме записи СЛУ имеет вид |
|
|
|
|
||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ai, j |
xj |
bi; |
i |
1,n |
. |
|
|
|
|
|
|
|
|
|||||||||
j i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Система называется обусловленной (не вырожденной, не особенной), если определитель системы 0, и тогда система имеет единственное решение.
Система называется не обусловленной (вырожденной, особенной), если = 0, и тогда система не имеет решений или имеет бесконечное мно-
14

жество решений. Для решения СЛУ широко применяют прямые и итерационные методы. Рассмотрим особенности решения СЛУ методом простых итераций .
3.1. Метод простых итераций для решения систем линейных уравнений
Формула итерационного процесса
|
|
|
|
|
|
|
1 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x(k) |
|
|
(b a x(k 1)) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
aii |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
i |
|
|
|
i |
j 1 |
ij j |
|
, i 1,n, |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где k = 1, 2, … – номер приближения. |
|
|
|
|
|
И |
|||||||||||||||||||||||||
|
|
x(0) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
– начальное приближение, i |
1,n. |
||||||||||||||||||||||||||||
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Условие завершения итерационного процесса: |
|
|
|
|||||||||||||||||||||||||||
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
||||||
где – требуемая точность; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Д |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k) |
(k 1) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
– оценка достигнутой точности, δ max |
|
xi |
xi |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
i 1,n |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 n |
|
|
|
|
С |
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
или |
|
δ |
|
|
|
x |
(k) |
x |
(k 1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
ni 1 |
|
|
|
i |
i |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Условие сходимости итерационного процесса (условие преобладания |
||||||||||||||||||||||||||||||
диагональных коэффициентов): |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
aii |
|
|
|
|
n |
aij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
i |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1,n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
i j
Если в полученных результатах значения δ > k > kmax, то задача не решена. Необходимо проверить условия сходимости или увеличить kmax.
15

3.2. Метод Зейделя для решения систем линейных уравнений
В формуле итерационного процесса метода простых итераций к моменту вычисления xi(k) уже вычислены значения x1(k),x2(k),...,xi− 1(k). Очевидно, что эти значения в большинстве случаев ближе к решению и их можно использовать для вычисления xi(k). Исходя из этого можно модифицировать формулу итерационного процесса метода простой итерации следующим образом:
|
1 |
|
i 1 |
n |
|
|
|
Xi(k) |
(bi ai, j xkj |
ai, j xkj 1), |
|
. |
|||
i 1,n |
|||||||
ai,i |
|||||||
|
|
j 1 |
j 1 1 |
|
|
||
|
|
1 |
n |
И |
|||
Условие завершения итерационного процесса и условия сходимости |
|||||||
метода простой итерации справедливы и для данного метода. Поэтому схе- |
|||||
|
|
|
Д |
||
ма алгоритма Зейделя отлична только формулой расчета нового приближе- |
|||||
ния: |
А |
|
|
||
|
|
|
|
||
xi |
|
(bi ai, j xj ), |
i 1,n . |
||
|
|||||
|
б |
|
|
|
|
|
ai,i |
j 1 |
|
|
|
i j
Данный метод позволяет достигать требуемой точности ε за меньшее число итераций, т.е. имеет лучшую сходимость.
Достоинства итерац онных методов для решения систем линейных уравнений следующие:
1. |
Погрешность округлен я не накапливается от итерации к итерации. |
2. Число итераций ипри n > 100 обычно меньше n , поэтому общее число |
|
действий меньше n3, т.е. меньше, чем в методе исключений Гаусса. |
|
3. |
Не требуется больший объем памяти. |
4. |
ИтерационныеСметоды особенно выгодны для систем с большим ко- |
личеством нулевых коэффициентов (систем с разряженной матрицей коэффициентов).
Недостаток − не всегда можно обеспечить сходность итерационного процесса. С увеличением размерности системы труднее выполнить линейные преобразования для обеспечения сходимости.
16

4.ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
При моделировании задача нахождения решения системы нелинейных уравнений является распространенной вычислительной задачей. Например, к решению таких систем сводятся расчеты фазового и химического равновесия многокомпонентных смесей, расчеты статических режимов многих технологических процессов и др.
Запишем систему n нелинейных уравнений с n неизвестными в общем
виде:
f1(x1, x2, …, xn) = 0; f2(x1, x2, …, xn) = 0;
…
fn(x1, x2, …, xn) = 0.
Эту систему можно записать в компактной, операторной форме: |
||||||||||||||
F(X) = 0, |
|
|
|
|
И |
|
|
|
|
|
||||
где |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
f1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Д1 |
|
|
|
|
|
|
|
||||
|
|
вектор-функция |
|
|
|
|
вектор неизвестных |
|||||||
F f |
2 |
|
X x2 |
|||||||||||
... |
|
|
А |
... |
|
|
|
|
|
|
|
|||
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
fn |
|
|
|
|
xn |
|
|
|
|
|
|
|
||
Решением системыиназывается набор значений |
x |
|
i |
|
|
|
||||||||
, |
1,n |
(вектор |
||||||||||||
|
|
С |
|
|
|
|
|
|
i |
|
|
|
|
|
X*), при которых все функции fi равны 0 (система нелинейных уравнений обращается в тождество).
Системы нелинейных уравнений могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение проводят в два этапа:
1-й этап – отделение решений.
2-й этап – уточнение всех или только нужных решений.
Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным [3].
Задача отделения решений реализуется только для системы двух уравнений с двумя неизвестными.
17
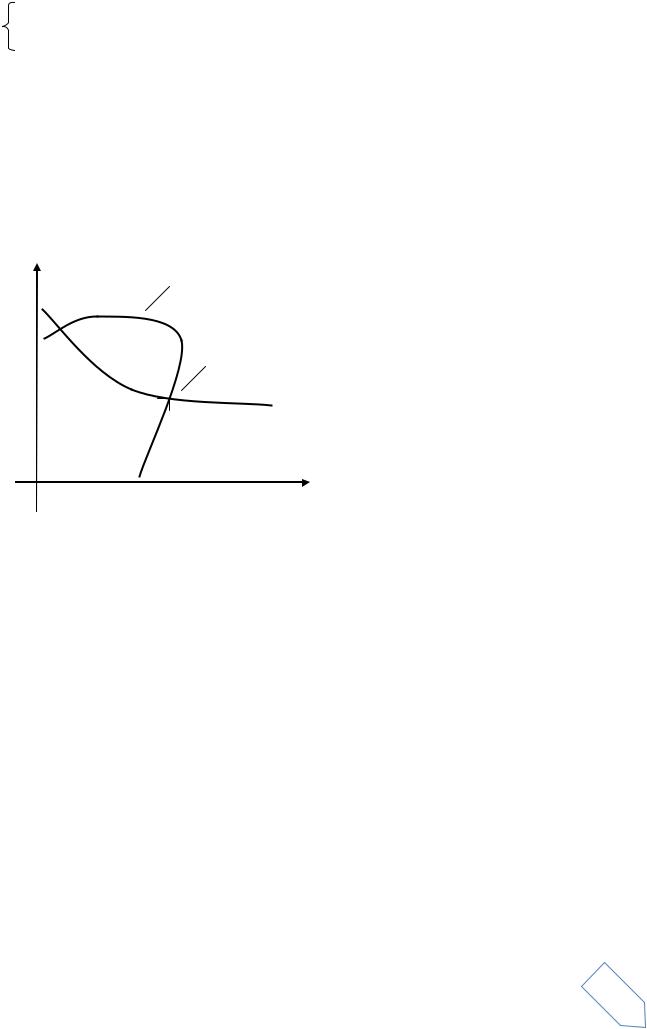
f1(x1, x2) = 0; f2(x1, x2) = 0.
Для этого необходимо в координатах (x1, x2) построить кривые f1(x1,х2) = 0, f2(x1,х2) = 0.
Точки пересечения этих кривых являются решениями системы (рис. 2). Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.
x2 |
|
|
|
f2(x1,х2)=0 |
|
|
Имеется два решения. |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
D1 – область существования первого |
|||||||
|
|
|
|
|
|
|
D1 |
|
|
|
|||||||||
b2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D1 = {a1 < x 1< b1 , a2 < x 2< b2}. |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
f1(x1,х2)=0 |
|
И |
|||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a1 x1* b1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|||||||
Рис. 2. Графическое отделение решение системы нелинейных уравнений |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
||||
Для систем с больш м ч слом неизвестных (n 3) общих методов оп- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
||
ределения области существован я решения нет. Поэтому при решении сис- |
|||||||||||||||||||
тем нелинейных уравненийиэта область обычно определяется при анализе |
|||||||||||||||||||
решаемой задачиС, например, исходя из физического смысла неизвестных проектируемого объекта.
Отделение решений позволяет:
1.Выявить число решений и область существования каждого из них.
2.Проанализировать возможность применения выбранного метода решения СНУ в каждой области.
3.Выбрать начальное приближение решения X(0) из области его сущест-
вования, так что X(0) D.
При отсутствии информации об области существования решения выбор начального приближения X(0) проводится произвольным способом и варьируется в ходе вычислительного эксперимента. Уточнение интересующего решения до требуемой точности ε производится итерационными методами.
18

4.1. Метод простых итераций для решения систем нелинейных уравнений
Метод простых итераций заключается в замене исходной системы уравнений эквивалентной системой X = Φ(X) и построении итерационной
последовательности
X(k) = Φ(X(k − 1)) , где k = 1, 2, 3,… − номер итерации, которая при k→∞ сходится к точному решению.
Здесь Φ(X) − вектор-функция; X(0) D – начальное приближение решения. В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид
xi.(k) |
= φi(x1(k− 1), x2(k− 1), … , xn(k− 1)), |
i |
|
|
И |
|||||||||||||||||||
|
|
|||||||||||||||||||||||
1,n. |
||||||||||||||||||||||||
Условие окончания расчета |
А |
|
|
|
||||||||||||||||||||
δ ≤ ε, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
||||||||||
где ε |
заданная точность решения; |
|||||||||||||||||||||||
δ = |
max | xi(k ) xi(k 1) | |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
i 1,n |
|
|
|
|
и |
|
|
|
|
|
|||||||||
или |
|
|
|
|
1 |
|
|
|
|
|
|
С |
б |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(k ) |
|
|
(k 1) |
|
|
|
|
|||||||||
δ = |
|
|
| xi |
|
xi |
|. |
|
|
|
|
|
|||||||||||||
n |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Итерационный процесс сходится к точному решению, если в окрестно- |
||||||||||||||||||||||||
сти решения соблюдаются условия сходимости: |
||||||||||||||||||||||||
n |
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1, |
i |
1,n |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
j 1 |
|
x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1, |
j 1,n |
. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
i 1 |
|
|
x j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, для уточнения решения методом простых итераций нужно найти такое эквивалентное преобразование, чтобы в области существования решения выполнялись условия сходимости.
19

4.2. Метод Ньютона для решения систем нелинейных уравнений
Идея метода заключается в линеаризации уравнений системы нелинейных уравнений, что позволяет свести исходную задачу к многократному решению системы линейных уравнений [3].
Пусть известно приближение xi(k) решения системы нелинейных уравнений xi*. Введем в рассмотрение поправку xi как разницу между решением и его приближением:
Δxi x*i xi(k) x*i xi(k) Δxi , i 1,n.
Подставим полученное выражение для xi* в исходную систему.
f (x(k) |
Δx , x(k) Δx |
,...,x(k) Δx ) 0; |
|
||||||||||
1 |
1 |
1 |
2 |
2 |
|
n |
|
n |
|
|
|
||
f |
2 |
(x(k) |
Δx , x |
(k) |
Δx |
2 |
, ...,x |
(k) |
Δx |
n |
) 0; |
||
|
1 |
1 |
|
2 |
|
|
n |
|
)И0. |
||||
… |
(x(k) |
|
|
(k) |
|
|
, ...,x(k) |
|
|
||||
f |
n |
Δx , x |
Δx |
2 |
Δx |
n |
|||||||
|
1 |
1 |
|
2 |
|
|
n |
|
|
|
|||
Неизвестными в этой системе нелинейныхД |
уравнений являются по- |
||||||||||||
задачу так же сложно, как и исходнуюА. Однако эту систему можно линеари-
правки xi. Для определения xi нужно решить эту систему. Но решить эту
зовать, и, решив ее, получ ть при лиженные значения поправок xi для
|
|
|
(k) |
|||
данного приближения, т.е. бxi . Эти поправки не позволяют сразу получить |
||||||
|
i |
и |
||||
точное решение x* |
, но дают возможность приблизиться к решению, – по- |
|||||
лучить новое приближение решения |
||||||
(k 1) |
(Сk) (k) |
|
|
|
||
, i 1,n. |
||||||
xi |
xi |
Δxi |
||||
Для линеаризации системы следует разложить функцию fi в ряды Тейлора в окрестности xi(k), ограничиваясь первыми дифференциалами.
Полученная система имеет вид
n f |
(x(k) |
,x(k) |
,...,x(k)) |
|
|
|
||
|
|
|
||||||
|
i |
1 |
2 |
n |
Δxi(k) fj(x1(k),x2(k),...,xn(k)), |
j 1,n. |
||
|
|
xi |
|
|||||
i 1 |
|
|
|
|
|
|
|
|
20

Все коэффициенты этого уравнения можно вычислить, используя последнее приближение решения xi(k). Для решения системы линейных уравнений при n = 2, 3 можно использовать формулы Крамера, при большей размерности системы n – метод исключения Гаусса.
Значения поправок используются для оценки достигнутой точности решения. Если максимальная по абсолютной величине поправка меньше заданной точности , расчет завершается. Таким образом, условие окончания расчета:
δ= max Δxi(k) ε.
i1,n
Можно использовать и среднее значение модулей поправок:
1 n | xi | . n i 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
В матричной форме систему можно записать как |
|||||||||||||||||||
|
|
W(X(k)) X(k) F(X(k)), |
|
|
|
|||||||||||||||
где |
|
|
|
|
|
|
|
|
f |
|
f |
|
|
Аf |
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
... |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
|
|
||||
|
|
|
|
fj |
|
|
|
С |
|
2бn |
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||
W(X) |
|
x |
|
|
|
... |
... ... |
|
... − матрица Якоби (производных); |
|||||||||||
|
|
|
|
|
||||||||||||||||
|
|
|
|
i |
|
n,n |
|
f |
n |
|
f |
n |
|
f |
n |
|
||||
|
|
|
|
|
|
|
|
|
x |
и... |
|
x |
|
|
||||||
|
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
n |
||
|
|
|
Δx(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X |
(k) |
|
Δx2(k) |
|
− вектор поправок; |
|
|
|
||||||||||||
|
... |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Δx(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(X) − вектор-функция;
W(X(k)) – матрица Якоби, вычисленная для очередного приближения. F(X(k)) – вектор-функция, вычисленная для очередного приближения.
Выразим вектор поправок ∆X(k):
X(k) W 1(X(k)) F(X(k)),
21

где W-1 – матрица, обратная матрице Якоби.
Окончательно формула последовательных приближений метода Ньютона решения системы нелинейных уравнений в матричной форме имеет
вид X(k 1) X(k) W 1(X (k)) F(X(k)).
Достаточные условия сходимости для общего случая имеют очень сложный вид и на практике проверяются редко. Нужно отметить, что метод сходится очень быстро (за 3 – 5 итераций), если det|W| 0 и начальное приближение X(0) выбрано близким к решению (отличаются не более чем на
10%).
Алгоритм решения методом Ньютона состоит в следующем:
1.Задается размерность системы n, требуемая точность ε, начальное приближенное решение X = (xi)n.
2.Вычисляются элементы матрицы ЯкобиИW = ( i xj)n,n.
3.Вычисляется обратная матрица W-1.Д
7. Оценивается достигнутая точность |
δ = max Δxi(k) или |
|||||
|
|
|
|
|
А |
i 1,n |
|
1 |
n |
|
|
|
|
|
i 1 |
| xi |. |
|
|
||
n |
|
|
||||
8. Проверяется услов е завершения итерационного процесса δ ≤ ε. |
||||||
Если оно не соблюдаетсяб, алгоритм исполняется снова с пункта 2. |
||||||
|
|
|
|
и |
|
|
|
|
|
С |
|
|
|
22

5.ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Уравнение, содержащее производные от искомой функции y = y(x), на-
зывается обыкновенным дифференциальным уравнением (ОДУ).
Общий вид дифференциального уравнения:
F(x,y,y ,y ,...,y(n)) 0,
где n – наивысший порядок производной, определяет порядок уравнения. Решением ОДУ называется функция y = y(x), которая после ее подста-
новки в уравнение обращает его в тождество.
|
Общее решение ОДУ имеет вид |
И |
|
|
y y(x,C1,C2,...,Cn), |
||
|
|
|
|
где C1, C2, …, Cn – постоянные интегрирования. |
|||
|
Частное решение получается из общего при конкретных значениях Ci, |
||
|
|
|
Д |
i 1,n. Эти значения определяютсябАиз n дополнительных условий. В качестве таких условий могутиыть заданы значения функции и ее производных при некоторых значен ях аргумента x, иначе говоря, в некоторых точках.
В зависимостиСот того, как заданы эти дополнительные условия, выделяют 2 типа задач:
Задача Коши. Все условия заданы в одной, начальной точке, поэтому они называются начальными условиями.
Краевая задача. Условия заданы в более чем одной точке, обычно в начальной и конечной. Условия в этом случае называются краевыми или граничными. Такая задача может возникнуть только при решении ОДУ с порядком выше первого.
Разработано множество методов решения подобных задач:
1. Графические методы. Например, метод изоклин − путем графических построений находят точки исходной функции и строят ее график.
2. Аналитические методы позволяют получить формулу исходной функции путем аналитических преобразований.
3. Приближенные методы позволяют получить приближенное аналитическое решение в результате принятых упрощений. К приближенным относятся асимптотические методы и метод малых возмущений.
23
