КР.КРАТ.ИНТ

К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-1

1. Вычислить интеграл по области, ограниченной прямыми

у=х, y=2x, x=2. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

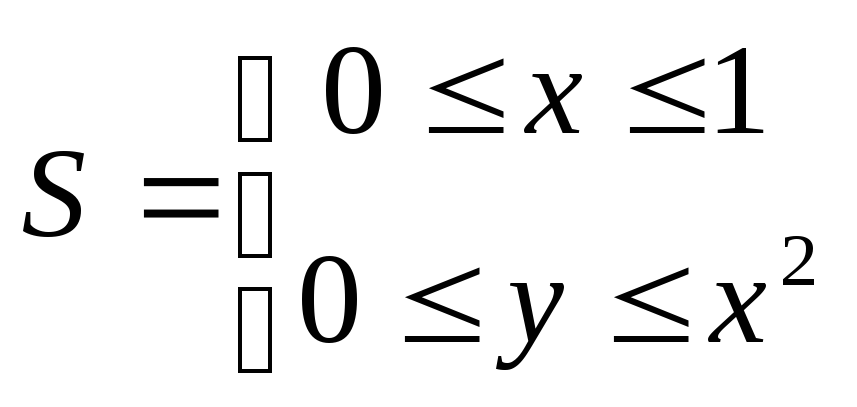К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-2

1. Вычислить интеграл по области, ограниченной прямыми

у= –х, y=2x, x=2. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

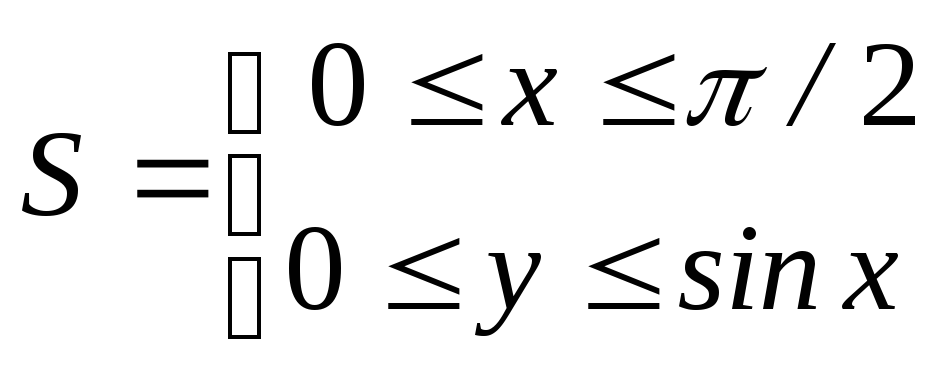К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-3

1. Вычислить интеграл по области, ограниченной прямыми

у=х/2, y=1, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

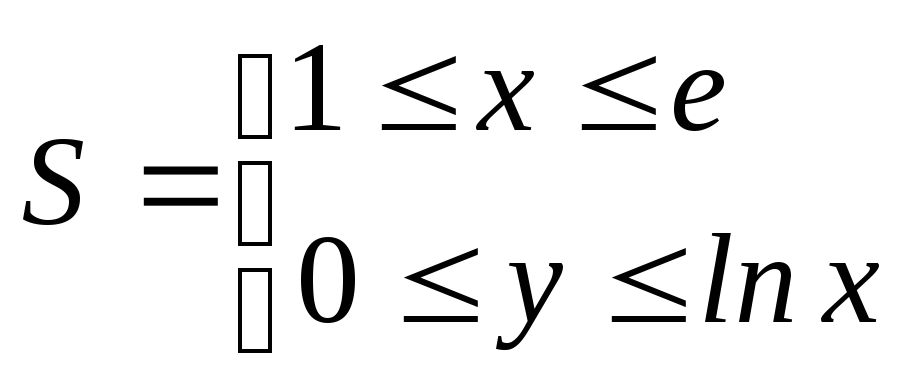К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-4

1. Вычислить интеграл по области, ограниченной прямыми

у=2–2х, y=0, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-5.

1. Вычислить интеграл по области, ограниченной прямыми

у=х, y=2–x, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

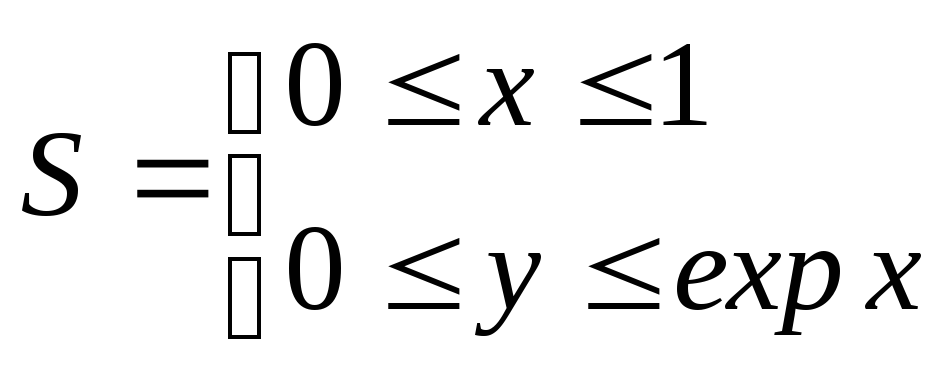К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-6

1. Вычислить интеграл по области, ограниченной прямыми

у=х, y=3x, x=1. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

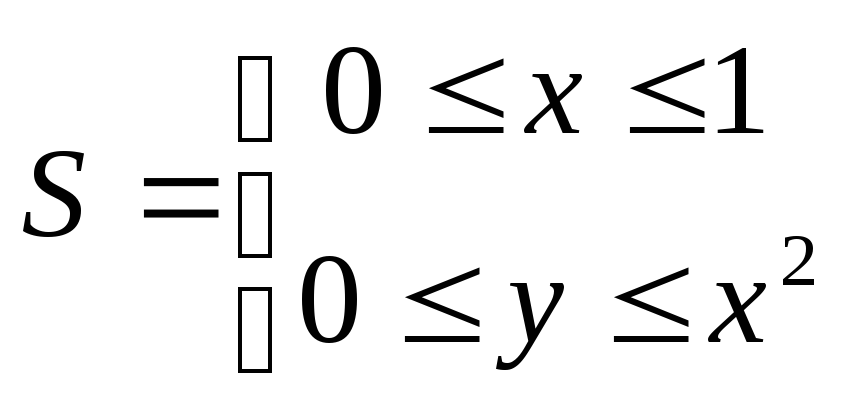К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-7

1. Вычислить интеграл по области, ограниченной прямыми

у= –2х, y=x, x=2. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

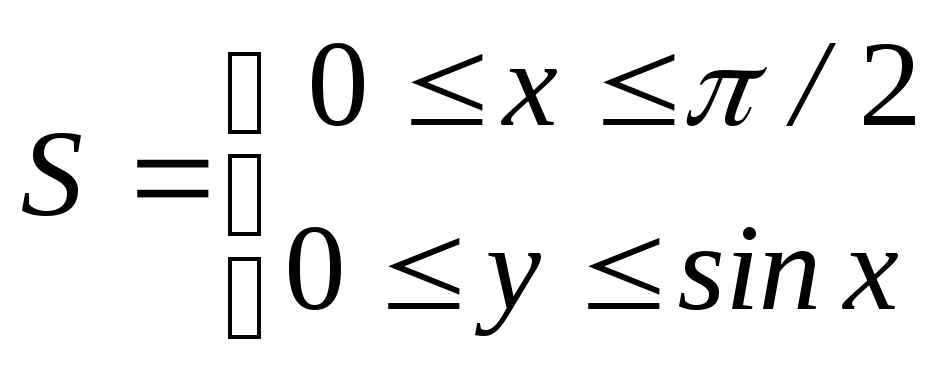К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-8

1. Вычислить интеграл по области, ограниченной прямыми

у=2х, y=2, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

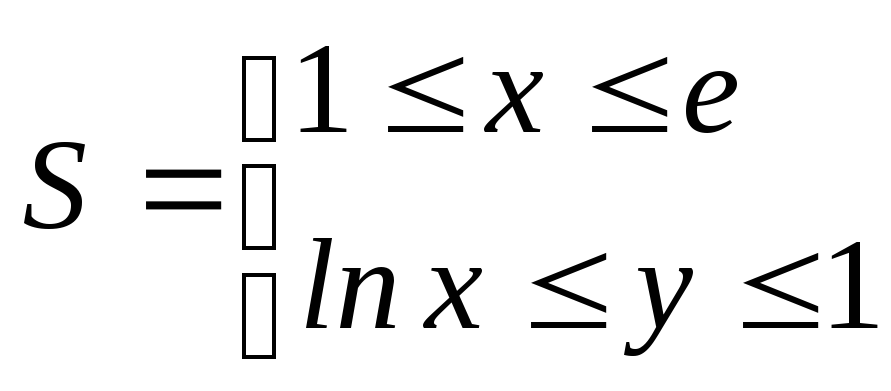К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-9

1. Вычислить интеграл по области, ограниченной прямыми

у=4–2х, y=0, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

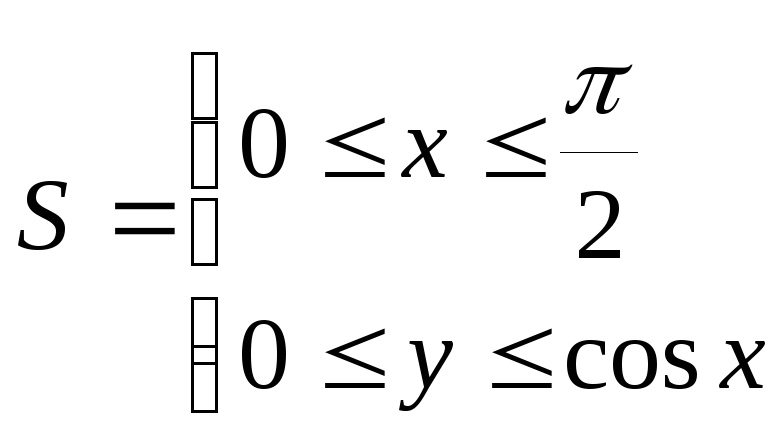К

КАНТ-2006

онтрольная работа на кратные интегралы

Краткий курс, 2 семестр, ВАРИАНТ-10.

1. Вычислить интеграл по области, ограниченной прямыми

у=2х, y=3–x, x=0. 2. Найти координаты центра тяжести этой области.

3. Вычислить интеграл по области .

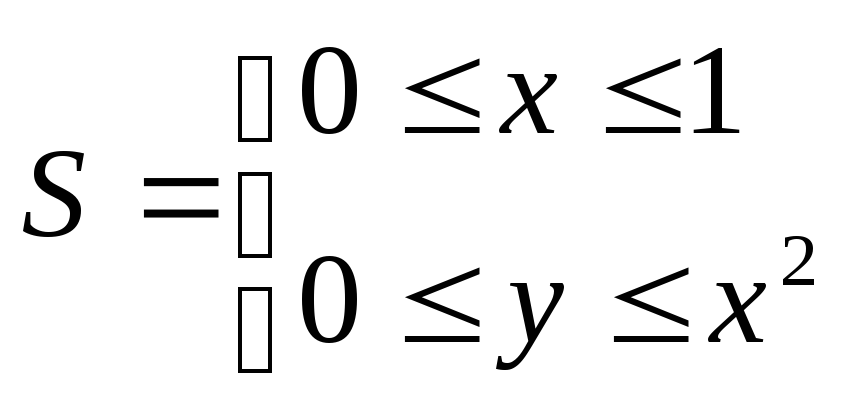ОТВЕТЫ К ВАРИАНТАМ

КОНТРОЛЬНОЙ РАБОТЫ НА КРАТНЫЕ ИНТЕГРАЛЫ

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .