1.1.3. Оценка устойчивости сау по ее частотным и логарифмическим частотным характеристикам

Понятие устойчивости САУ связано со способностью системы возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния.

Оценка устойчивости САУ производится по алгебраическим или частотным критериям устойчивости, описанным в [1,2,3]. К частотным критериям устойчивости относятся:

1. критерий устойчивости Михайлова;

2. критерий устойчивости Найквиста;

3. оценка устойчивости САУ по ее ЛЧХ.

Если в характеристический полином замкнутой САУ

(21)

где ,–полиномы числителя и знаменателя передаточной функции разомкнутой системы , подставить значение , то получим характеристический комплекс .

(22)

где его вещественная и мнимая части определяются как:

	(23)
	(24)

а функции и представляют собой модуль и аргумент (фазу) характеристического комплекса

При изменении частоты от 0 до  вектор из комплексной плоскости X-Y опишет своим концом кривую (годограф вектора ), называемую кривой Михайлова (рис. 1.14).

Критерий устойчивости Михайлова формулируется таким образом :

Для устойчивости линейной САУ n-го порядка необходимо и достаточно, чтобы кривая Михайлова при изменении частоты от 0 до бесконечности проходила последовательно n квадрантов в направлении против часовой стрелки, окружая начало координат, причем ее конец должен уходить в бесконечность в том квадранте комплексной плоскости X-Y, номер которого равен степени характеристического уравнения n.

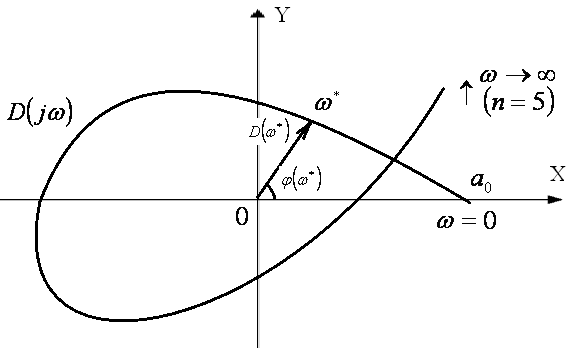
Рис. 1.14.

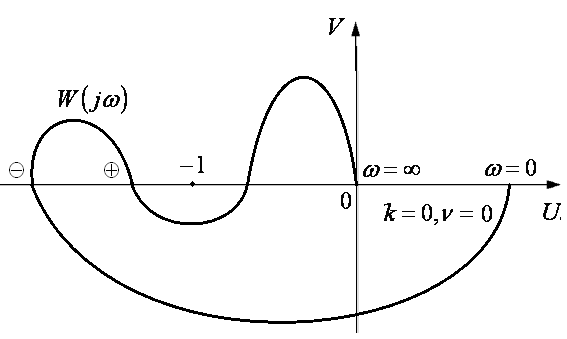
Критерий устойчивости Найквиста в общем случав формулируется следующим образом : - для устойчивости замкнутой САУ необходимо и достаточно, чтобы разность между числами положительных (сверху вниз) и отрицательных (снизу вверх) переходов AФЧХ разомкнутой системы через ось абсцисс левее точки при изменении частоты и от 0 до  была равна , где k - число корней характеристического уравнения разомкнутой системы с положительной вещественной частью. При этом начальная точка характеристики на оси абсцисс левее точки считается как половина перехода. Для систем, находящихся в разомкнутом состоянии на границе устойчивости, т.е. 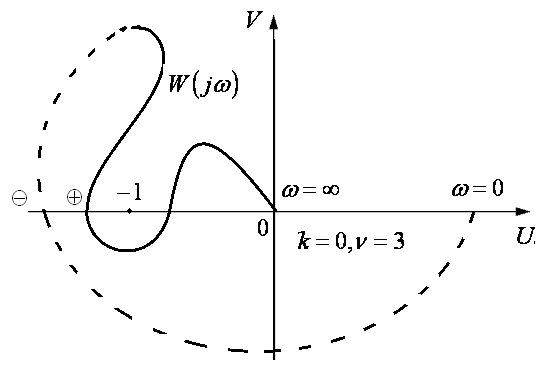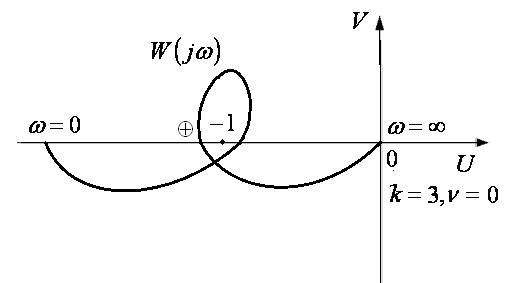имеющих  нулевых корней характеристического уравнения, число k считается равным нулю, а АФЧX берется с дополнением в бесконечности (рис. 1.15, 1.16, 1.17).

Рис.15.	Рис.16.
Рис.1.17.

На основании критерия устойчивости Найквиста могут быть сформулированы требования, которым должны удовлетворять логарифмические частотные характеристики разомкнутой системы для того, чтобы она была устойчива в замкнутом состоянии. Это связано с тем, что в точках пересечения АФЧХ отрезка ЛАЧХ положительна, а ЛФЧХ пересекает прямую (-180°) снизу вверх (положительный перевод) или сверху вниз (отрицательный переход).

Требования к ЛАЧХ и ЛФЧХ в общем случае формулируются следующим образом: для устойчивости замкнутой САР необходимо и достаточно, чтобы разность между числами положительных и отрицательных переходов ЛФЧХ разомкнутой системы через прямую (-180°) при тех значениях частоты , для которых ЛАЧХ разомкнутой системы положительна, была равна , где k - число корней характеристи­ческого уравнения разомкнутой системы с положительной вещественной частью. При этом начало ЛФЧХ в бесконечно удаленной точке =0 на прямой (-180°) считается за половину перехода. В случае астатических систем (0) при подсчете точек пересечения ЛФЧХ с прямой (-180°) надо иметь в виду, что если начало ЛФЧХ лежит ниже прямой (-180°) (что соответствует АФЧХ на рис,16), то в число отрицательных переходов надо включать бесконечно удаленную влево точку =0.(рис 1.18)

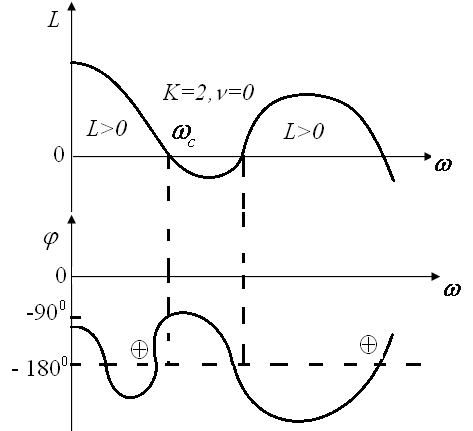
Рис.1.18.