3. Циклические коды Хемминга

Циклические коды Хемминга образуют подмножество циклических (n, k) – кодов. Они обладают всеми свойствами кодов Хемминга и еще дополнительными полезными свойствами.

При определении методов построения циклических кодов используются понятия неприводимых и примитивных многочленов.

Определение. Многочлен g(х) степени m называется неприводимым в поле GF(2)={0, 1}, если он не делится ни на какой многочлен с коэффициентами из GF(2) степени меньшей m, но большей нуля.

Определение. Неприводимый многочлен g(х) степени m называется примитив­ным, если наименьшая степень n, при которой многочлен хⁿ+ 1 делится на g(х) без остатка, равна n=2^m-1.

Другими словами, многочлен g(х), степени m называется примитивным, если

делится на g(х) без остатка,

а не делится наg(х) ни для какого значения .

Например, многочлен 1 + х² + х³ примитивен:

он делит х⁷ + 1, но не делит x^j+1 при j < 7.

Примитивен также многочлен 1 + х³ + х⁴ :

он делит х¹⁵ + 1, но не делит x^j+1 при j < 15.

С помощью порождающих многочленов g(х) можно строить порождающие и проверочные матрицы и таблицы синдромов для декодирования.

Утверждение. Для любого целого положительного числа m существует совершенный (n,k)-код Хэмминга, в котором n=2^m-1 или k =2^m-m-1.

Расширенные коды Хэмминга. Полезное расширение кодов Хэмминга заключается в дополнении кодовых векторов дополнительным двоичным разрядов так, чтобы число единиц в каждом кодовом слове было четным. Такие коды обладают двумя полеными свойствами:

1. Длины кодов увеличиваются с 2^n-1 до 2ⁿ, что удобно с точки зрения хранения и передачи информации,

2. Минимальное расстояние для расширенных кодов Хэмминга равно четырем, а не трем, что позволяет обнаруживать трехкратные ошибки.

4. Критерии оценки помехоустойчивости.

В качестве численных характеристик помехоустойчивости кода используются:

1. Помехоустойчивость кода

- собственное количество информации в факте необнаружения ошибки.

2. Коэффициент обнаружения

,

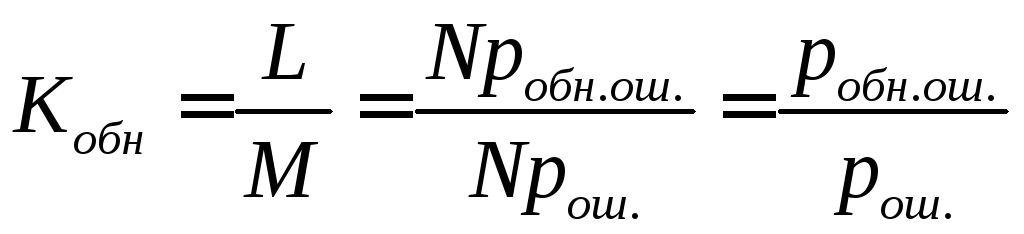где M – ожидаемое общее число искаженных кодовых слов,

L - ожидаемое число исправленных кодовых слов,

N – число всех кодовых слов,

р_ош. – число вероятность появления ошибки,

р_обн.ош. – вероятность обнаружения и исправления ошибки.

Если R - ожидаемое число неисправленных искаженных кодовых слов, то R=M-L и .

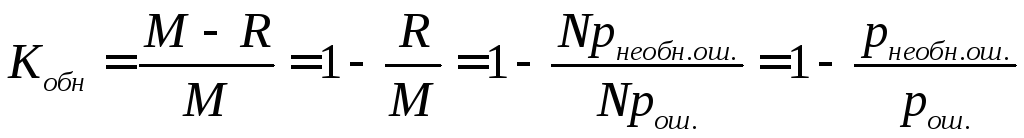Пусть вероятность искажения одного символа кода равна р.Найдем вероятности передачи без ошибки р₍₀₎ и однократной ошибки р₍₁₎ при которых гарантируется правильная передача простым кодом Хемминга.

.

(Для расширенного кода Хемминга выявляется и двухкратная ошибка с вероятностью ).

Вероятность ошибочной передачи – все остальное. С учетом того, что при больших n: (по разложению (1-р)ⁿ в ряд Тейлора):

Если исправляется одна ошибка, то по теоремам Хемминга можно одновременно обнаружить 2 ошибки. Расширенный код Хемминга позволяет дополнительно обнаружить еще одну ошибку. Вероятность появления необ­наруживаемых 3-х и 4-х кратных ошибок

и , где.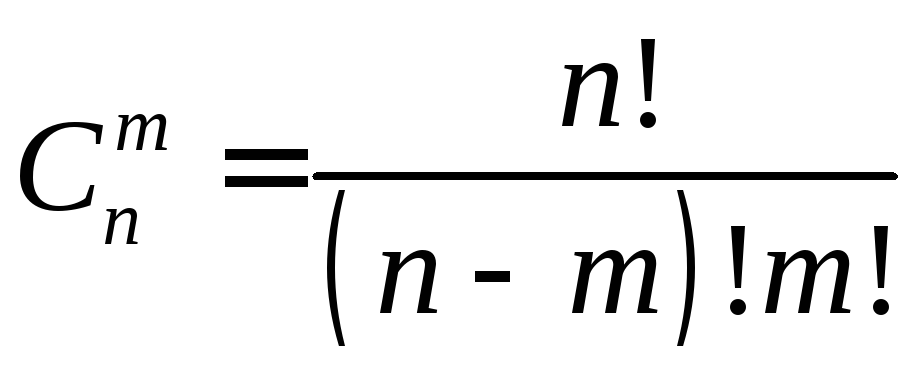

При малых значениях вероятности р при вычислении р_{необн.ош.} ошибки большей кратности можно не учитывать в силу их малой вероятности.

5. Определение значности кода.

Первым шагом при построении кода являеся определение значности кода, то есть количества символов n в блоке помехоустойчивого кода и количества символов k исходного файла (информационных символов). Они определяют корректирующие способности кода. При этом каждый блок содержит m проверочных символов.

Для заданного образующего полинома степени m количество добавляемых при кодировании проверочных символов равно m. Коды Хемминга исправляют одиночную ошибку в блоке. Это коды с . Соотношения для параметров кодаn, k и m для них имеют вид:

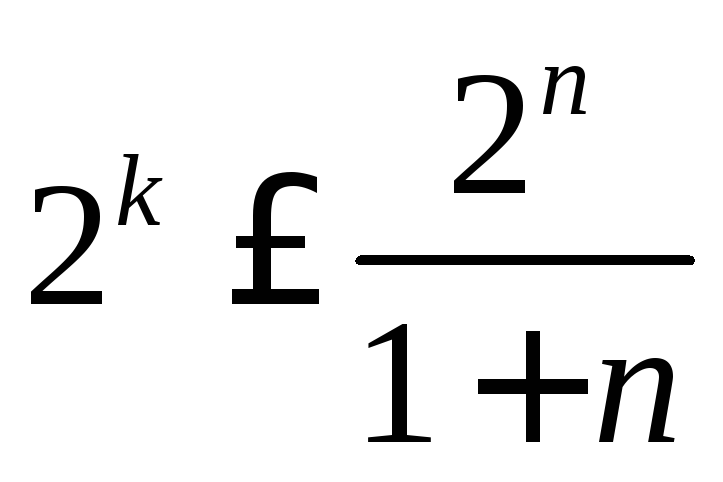и .

Отсюда длина блока выбирается из неравенства

n ≤ 2^m – 1,

а количество информационных символов в блоке k = n - m.

Коды, удовлетворяющие этому условию являются квазисовершенны­ми. Решить это уравнение относительно n здесь сложно, поэтому определим из него m=n-k:

(*).

Таблица. Соотношения между параметрами помехоустойчивых кодов.

n	2	3	4	5	6	7	8	9	…	15	16	…	30	31	32	…	63	64	…	127	128
m	2	2	3	3	3	3	4	4	…	4	5	…	5	5	6	…	6	7	…	7	8
k	0	1	1	2	3	4	4	5	…	11	11	…	25	26	26	…	57	57	…	120	120

Для того чтобы количество информационных символов было максимальным при заданном количестве проверочных символов желательно выбирать общую длину блока n таким образом, чтобы неравенство (*) превратилось в строгое равенство. Коды, удовлетворяющие этому условию являются совершенны­ми.