6. Матричное задание циклических кодов.

Циклический код может быть задан порождающей и проверочной матрицами. Для их построения достаточно знать порождающий g(x) и проверочный h(x) многочлены. При этом проверочный многочлен вычислякется по порождающему:

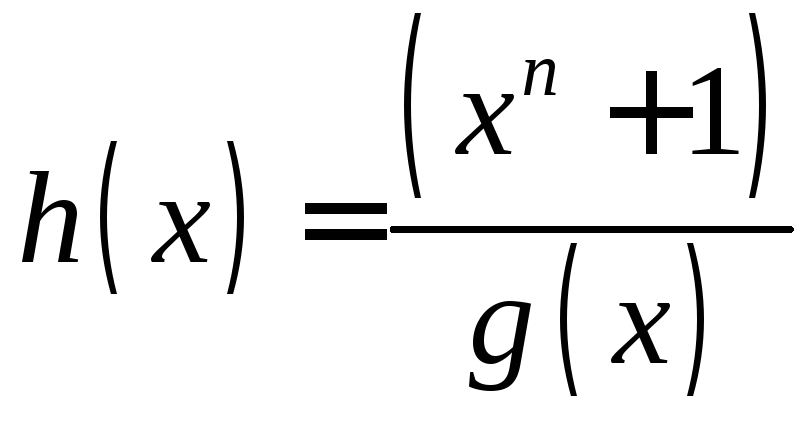
Для несистематического циклического кода матрицы строятся цик­лическим сдви­гом порождающего и проверочного многочленов, т.е. путем их умножения на x.

При построении матрицы H_(n,k) старший коэффициент многочлена h(x) располагается справа.

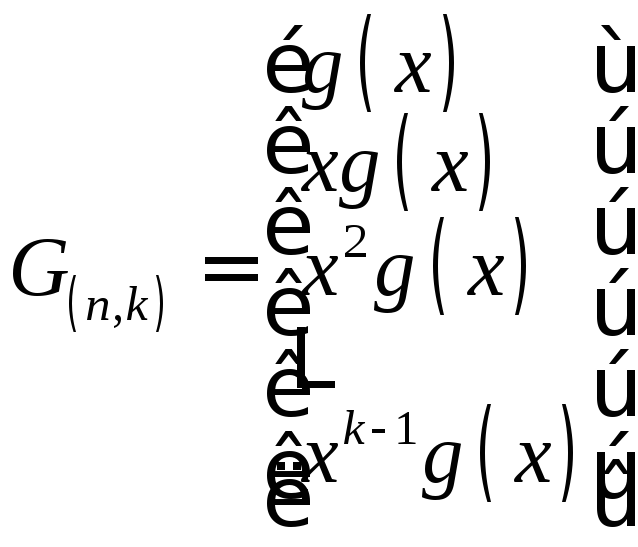и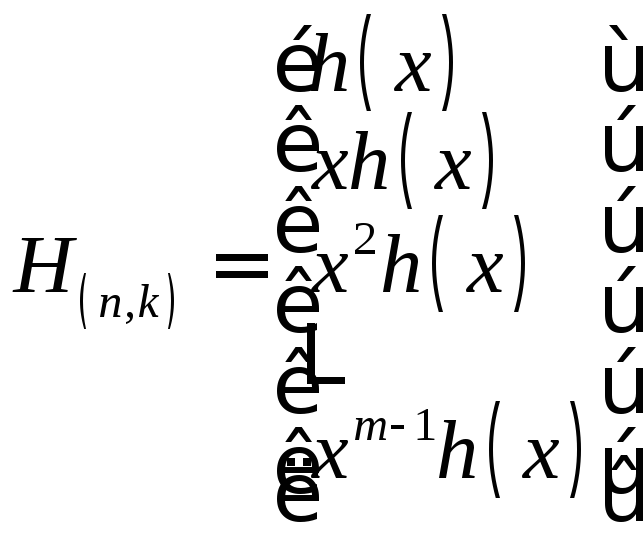

Например представим в матричном виде. циклический (7,4)-код с порожда­ющим многочленом g(x)=x³+x+1 и проверочным многочленом

.

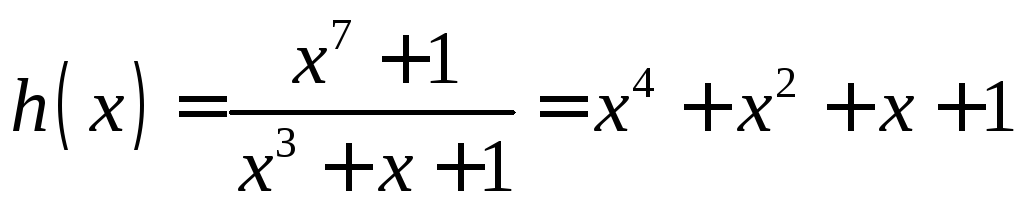Порождающая G_(7,4) и проверочная H_(7,4) матрицы (n=7,k=4)-кода имеют вид:

,

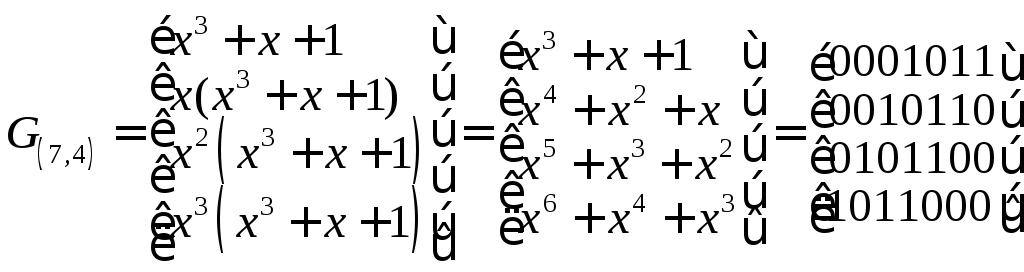
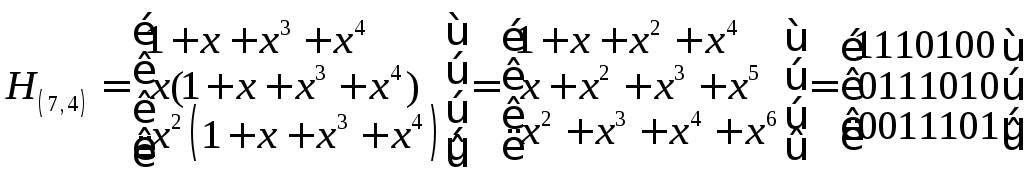Построенные таким образом матрицы не имеют систематического вида. Для получения матрицы G_(n,k) циклического кода в систематическом виде, то есть в виде , гдеI_k - единичная матрица; R_k,m - прямоугольная матрица, необходимо найти матрицу R_k,m. Ее строки r_i(x) (i=1, … ,.k) определяются следующими полиномами:

,

где R_g(x)[ ] – обозначает операцию получения остатка от деления на g(x), и a_i(x) – полином, соответствующий значению i-й строки матрицы I_k. Так как a_i(x)=x^k-i, то получаем, что a_i(x)x^m = x^m+k-i = x^n-i, то есть .

Для нашего примера. Матрица G_(n,k) для (7,4)-кода на основе порождающего многочлена g(x)=x³+x+1 в систематическом виде , строится так:

Поскольку ,

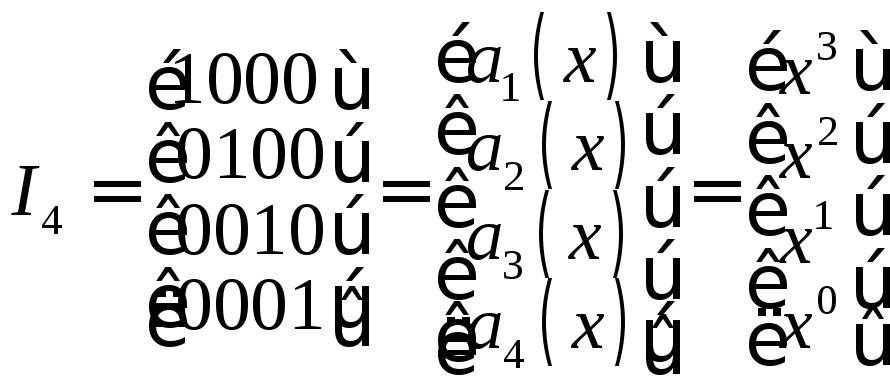о

1000000 1011

 1011

1100 3-я и 4-я строки

1011

1110 2-я строка

1011

101 1-я строка

пределимR_4,3, используя формулу . Первую строку получаем делением

и

x⁶ x³+x+1 x⁶+x⁴+ x³ x³+x+1

x⁴+ x³ (110) и (011)

x⁴+ x²+x .

x³+x²+x (111)

x³+ x+1 .

x² +1 (101)

ли

(101).

Для получения второй строки не надо снова делить углом, так как делимое совпадет с предыдущим случаем с точностью до последнего нуля. Поэтому для получения остатка от деления на х⁵ достаточно взять предпоследний остаток в предыдущем делении на х⁶ не снося очередной нуль. Таким способом определяется (111),(110) и(011). Последние две строки получаются из одного и того же остатка, убирая последовательно по одному нулю (добавляя при необходимости слева нули до трех символов), так как в этой строке были при делении снесены два нуля.

В результате получаем

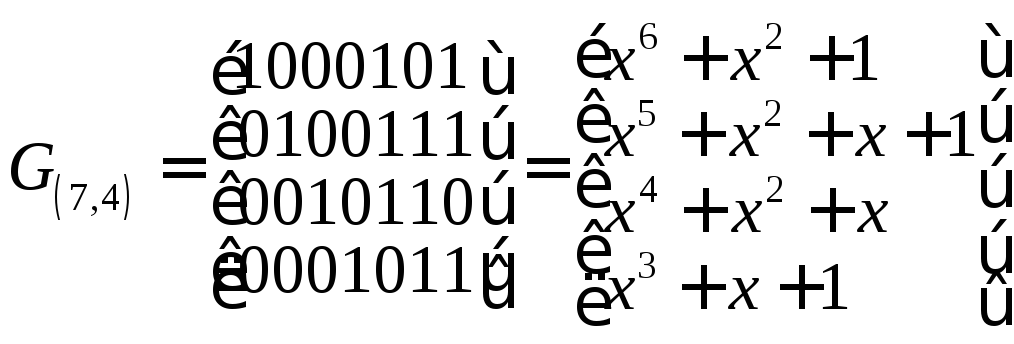
Количество исправляемых ошибок в блоке определяется минимальным рассстоянием Хемминга d_min между разрешенными кодовыми словами. Минимальное расстояние для (n,k)-кода равно наименьшему числу линейно зависимых столбцов проверочной матрицы. Для нашего примера d_min (5,3)=2.

Проверочная матрица в систематическом виде строится на основе матрицы G_(n,k), а именно: .

Для нашего примера. Для нашего кода матрица H_(n,k) будет иметь вид:

.

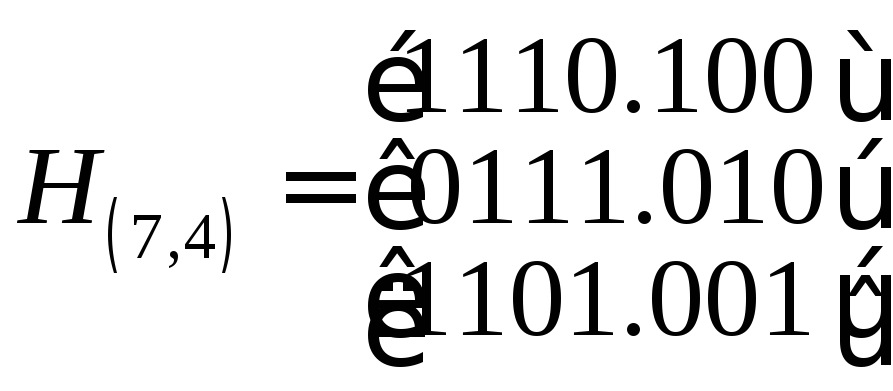Между порождающей и проверочной матрицами в систематическом виде существует однозначное соответствие, а именно , где0 – матрица размерности kxm, у которой все элементы равны нулю.

7. Кодирование и декодирование.

Кодирование при матричном представлении кода ведется путем умножения вектора, соответствующего информационному слову, на порождающую матрицу. Результат операции дает слово помехоустойчивого кода.

Для нашего примера кодирование блока информационных символов Р=[110] дает блок помехоустойчивого кода U =11010]:

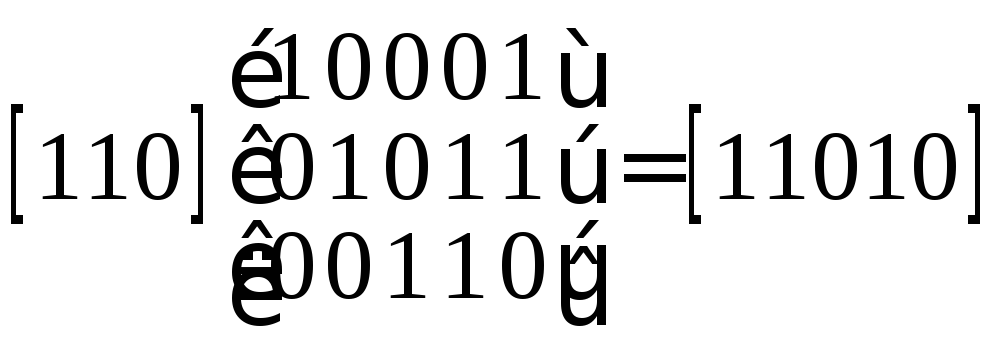
Произведение любого разрешенного кодового слова U на транспонированную проверочную матрицу дает вектор длины (n-k) с нулевыми координатами

.

Для нашего кода это произведение дает .

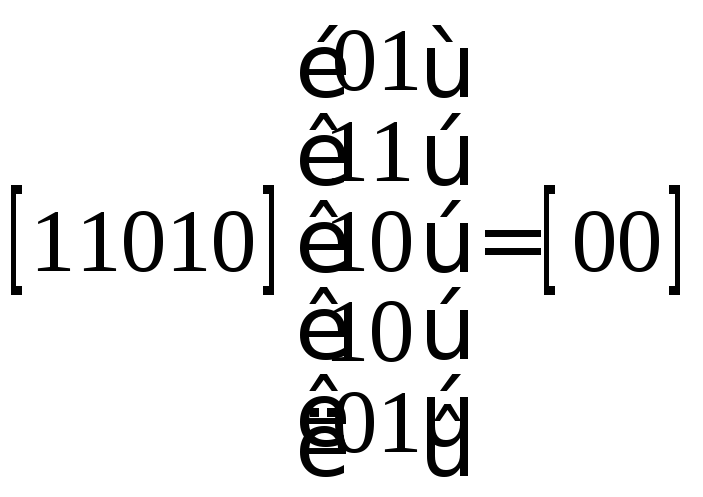Таким образом проверка правильности принятого кода состоит в умножении вектора этого кода на проверочную матрицу. Нулевой вектор результата означает отсутствие ошибки передачи данных.

Произведение неразрешенного, т.е. с ошибкой, кодового слова на транспонирован­ную проверочную матрицу называется синдромным вектором и обозначаетсяS.

Появление отличного от нулевого синдромного вектора является признаком ошибки. В этом случае декодирование предполагает исправление ошибки или выдачу сообщения о неисправимой ошибке.

Например. Пусть при передаче ко­дового слова, полученного в предыдущем примере, допущена одна ошибка и принято = [11000], то есть во втором символе ошибка. Соответствующий полином:=x⁴+x³.

В

: 11000 1101

 1101

10

s(x)=x

ычисляем синдром делением его на образующий полиномg(x)=x³+x+1. Если нас интересует только остаток от деления, то мож­но вычис­лять его в столбик.

e(x)
x0=1	1
x	x
x2	x2
x3	x+1
x4	x2+ x
x5	x2+x+1
x6	x2+1

Составим табли­цу синдро­мов для однократных оши­бок. Все возможные вектора ошибок для искажений единственного символа в блоке будут иметь по одной единичной координате при всех остальных нулевых. Им соответствуют всевозможные одночлены, для которых вычисляем остатки от деления на и получается искомая таблица.

Замечание. при построении этой таблицы можно воспользоваться результатами деления xⁿ на g(x), полученными при построении порождающей матрицы. Для синдромов, имеющих степень меньше m, синдромный полином совпадает с полиномом ошибки.

В нашем случае находим по таблице, что e(x) = x и исправляем ошибку:

u(x)=+e(x)=x⁴+x²+x+1.

Появление синдромного вектора, не содержащегося в таблице, означает, что произошло более одной ошибки и требует соответствующего сообще­ния о неисправимой ошибке в блоке. Ошибка в блоке останется необнару­женной в том и только в том случае, если многочлен, соответствующий вектору ошибки делится на g(x) без остатка, то есть если вектор ошибки совпадет с разрешенным кодовым словом.

16