Математическое моделирование в процессах разработки и нефте-газодобычи

СПБГУАП| Институт 4 группа 4736

Резюме

Цель работы продемонстрировать основные понятия теории фильтрации жидкости на примере вывода и решения уравнений однофазного течения однородной жидкости для различных условий. Произведен вывод решений, описывающих производительность одно- и многопластовой скважины с различными условиями на внешней границе пласта на неустановившемся режиме.

В работе показано качественное отличие многопластовой системы от однопластовой системы с осредненными параметрами. На основе построенной модели показано, как по данным гидродинамических исследований выявить наличие ограниченных пропластков,

оценить гидродинамическую согласованность пласта.

3

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

1.Введение в математические модели и математический аппарат теории фильтрации

1.1.Уравнение пьезопроводности

Для описания процессов фильтрации жидкости в пласте используют математическую модель, в основе которой лежат несколько предположений: 1) добыча происходит на упругом режиме фильтрации, то есть допустимо считать, что в обычных интервалах изменения пластового давления плотность жидкости и пористость среды линейно зависят от давления [1]; 2)скорость фильтрации прямо пропорциональна градиенту давления,то есть выполняется закон Дарси:

При вышеизложенных предположениях распределение давления в пласте в любой момент времени описывается с помощью уравнения пьезопроводности, которое в случае наличия анизотропии по проницаемрости имеет вид [1]:

пористой среды.

В случае наличия распределенных стоков и источников в фильтрационном потоке уравнение пьезопроводности примет следующий вид:

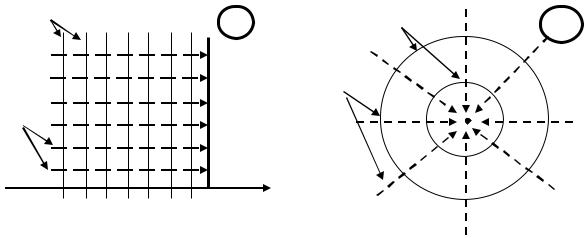
Рассмотрим скважину в центре однородного изотропного кругового пласта с отсутствием непрерывно распределенных стоков и источников (см. Рисунок 1.1), в случае наличия плоскорадиальной симметрии уравнение (1.3) имеет вид [1]:

4

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

re

Рисунок 1.1. Скважина в центре однородного изотропного кругового пласта

1.2.Начальные и граничные условия

Как уже было сказано, процесс фильтрации описывается уравнением пьезопроводности. Решение задачи фильтрации в однофазном случае в какой-либо области сводится к задаче решения соответствующего уравнения пьезопроводности, то

частных производных также называется интегрированием этого уравнения. Для того чтобы проинтегрировать уравнение пьезопроводности, необходимо также знать граничные и начальные условия [2].

Начальное условие заключается в задании начального распределения давления в пласте (то есть распределение давления на момент пуска скважины в работу), обычно считают, что пласт вначале невозмущен – когда давление во всех точках пласта одинаково

и равно начальному среднему пластовому давлению:

Граничные условия задаются на скважине и на границах пласта. На границах пласта чаще всего рассматриваются так называемые условия 1-го и 2-го родов [2]. Граничное условие 1-го рода – это условие поддержания постоянного давления на данной границе,

Граничные условия 2-го рода – это условия поддержания постоянного значения

производной давления, то есть поддержания постоянного потока через границу пласта.

Это условие используется, в частности, при описании пластов с отсутствием перетока через границу (значение производной в этом случае равно нулю):

5

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Также, как будет показано далее, данное условие может быть использовано при описании поведения скважины на псевдоустанвившемся и установившемся режимах в системе разработки.

Существуют еще граничные условия 3-го рода – условия связи давления и производной давления по координате (то есть связь между давлением и потоком через границу пласта)[5]:

В системе заводнения для корректного описания процесса взаимодействия скважин,

как на неустановившемся, так и на псевдоустановившемся и установившемся режимах необходимо использовать, как будет показано далее граничные условия 4-го рода [3],[4] –

условия сопряжения зоны закачки и зоны добычи.Конкретный вид данных граничных условий будет рассмотрен далее.

Также необходимо задать граничное условие на скважине. В зависимости от задания граничного условия на скважине, математические модели работы скважины классифицируются на модели постоянного давления и модели постоянного дебита. В

случае, когда на скважине поддерживается постоянное забойное давление (граничное условие 1-го рода), используется модель постоянного давления, а граничное условие выглядит следующим образом:

Модель постоянного дебита используется, соответственно, когда на скважине задано условие 2-го рода – поддерживается постоянный дебит и представляет собой закон фильтрации Дарси .

где Cs - коэффициент послепритока.

Модель постоянного дебита лучше применять, если имеется технические ограничения по добыче: это может быть предельная пропускная способность поверхностного обустройства, законодательные ограничения на максимальный дебит.

6

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Модель постоянного давления лучше применять в долгосрочном режиме работы скважины, когда дебит меняется сильно, а забойное давление остается приблизительно на одном уровне.

Необходимо упомянуть, что вообще говоря, на скважине меняется как забойное давление так и дебит, поэтому корректнее предположить, что дебит связан с давлением некоторой связью, например – в некоторых случаях с большой точностью можно аппроксимировать эту связь - линейной зависимостью (в первом приближении). Работа скважины с граничным условием 3-го рода, то есть с условием линейной связи забойного давления с дебитом рассматривается в статье [7]. Также есть ряд публикаций,

посвященных работе скважины при условии, что их дебит – есть некоторая функция

1.3.Способы интегрирования уравнения пьезопроводности

Существуют различные способы нахождения решений уравнения пьезопроводности.

Широкий обзор методов решения уравнения пьезопроводности можно найти в книгах [9], [1], [10], а также [2].

1.3.1. Фундаментальные решения

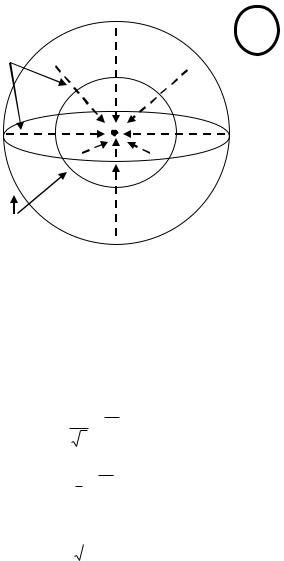
Рассмотрим одномерные потоки. В «одномерных» потоках все характеристики потока (давление, скорость фильтрации и т.д.) зависят не более чем от одной координаты.

Примерами одномерных потоков в могут служить: 1) Прямолинейно-параллельный поток

2) Плоскорадиальный поток (рисунок) 3) Сферический радиальный.

Траектории

Траектории

X

7

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

в)

Траектории

Изобары

Рисунок 1.2. Одномерные потоки в пространстве: а) одного б) двух и в) трех измерений.

В этих простейших случаях интегрирование уравнения пьезопроводности для точечного источника в бесконечном пласте сводится к интегрированию по времени фундаментального решения, которое математически описывается формулой для случаев пространства одного, двух и трех измерений следующими формулами [1], [2], [5]:

Физический смысл фундаментальных решений заключается в том, что они представляют собой распределение падения давления в бесконечном пласте в любой момент времени после мгновенного включения в пространстве соответственно бесконечного плоского, бесконечного линейного или точечного источника или стока [1].

Фундаментальные решения уравнения пьезопроводности были впервые получены Лапласом, Рэлеем и Томсоном. Для того чтобы решить уравнение пьезопроводности (то есть найти динамику давления в каждой точке пласта в любой момент времени – найти функцию p r,t ) для простейших случаев одномерных потоков в бесконечном пласте достаточно проинтегрировать соответствующее фундаментальное решение по времени.

В некоторых случаях, например, если необходимо решить уравнение пьезопроводности для цилиндрического поверхностного стока или источника – можно воспользоваться методом интегрирования соответствующего фундаментального решения по координате [1], тем самым получив фундаментальное решение для стока

(поверхностного или протяженного) сложной формы.

8

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

1.3.2. Свойство автомодельности

Некоторые задачи теории неустановившейся фильтрации можно решить, используя свойства автомодельности (если таковые имеются в данной задаче). Согласно [11]

определение автомодельности звучит следующим образом: «Явление, развивающееся во времени, называется автомодельным, если распределения его характеристик в разные моменты времени получаются одно из другого преобразованием подобия». Г.И.

Баренблатт в своей монографии [11] успешно использовал свойства автомодельности при интегрировании как линейных, так и нелинейных дифференциальных уравнений (в случае нелинейных дифференциальных уравнений имеет место введненная Баренблаттом так называемая «автомодельность второго рода»).

В самом простом случае свойство автомодельности заключается к возможности свести уравнение в частных производных с соответствующими начальными и граничными условиями от нескольких переменных, например, от времени и координаты, к уравнению от безразмерной комбинации этих переменных, в уравнении при этом уменьшится количество переменных. В частности, уравнение пьезопроводности для прямолинейно-

параллельного потока (если записать его относительно перепада давления):

обладает свойством автомодельности. Введя замену переменных:

где p x,t Cf w . Уравнение (1.18) называется сопряженным уравнением (1.15).

1.3.3. Метод Фурье разделения переменных

Также в некоторых случаях при интегрировании уравнения пьезопроводности можно воспользоваться методом разделения переменных. Суть метода заключается, в том что от уравнения пьезопроводности, выполнив соответствующую замену переменных, можно перейти к двум дифференциальным уравнениям, называемыми сопряженными данному,

имеющим более простой вид. Решение при этом ищется в виде:

9

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

То есть искомая функция представляется в виде произведения функции, зависящей

только от времени и функции, зависящей только от координат (откуда и пошло название метода).

В простых случаях – мы можем сразу найти вид функций r и t . В более общем случае – необходимо воспользоваться свойством линейности уравнения пьезопроводности, а именно – искать общее решение в виде суммы сходящегося ряда частных решений. Подробное описание метода разделения переменных можно найти в [1], [2] и [5].

1.3.4. Метод интегральных преобразований

При решении неавтомодельных задач теории неустановившейся фильтрации крайне полезны методы операционного исчисления – различные интегральные преобразования. С

помощью таких преобразований интегрирование уравнений в частных производных сводится к интегрированию обыкновенных дифференциальных уравнений.

В общем случае интегральное преобразование имеет вид [9], [12]:

уравнение имело более простой вид. Предполагается, что существует формула обращения:

контурным.

Широкое распространение при решении задач неустановившейся фильтрации

получило преобразование Лапласа, задаваемое следующей формулой [12], [9]:

i

Математически смысл решения с помощью преобразования Лпаласа заключается в переходе уравнения пьезопроводности и соответствующих граничных и начальных

10

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

условий в пространство Лапласа, где уравнение имеет более простой вид, затем – получению решения в пространстве Лапласа, а затем в обратном переходе в обычные координаты с помощью обратного преобразования Лапласа.

Иногда произвести аналитическое интегрирование (1.23) для обратного преобразования Лапласа – крайне тяжело, поэтому для практических целей иногда удобно пользоваться численным обратным преобразованием Лапласа [13], например, в задачах с граничными условиями 4-го рода – по построению модели работы многопластовой скважины [14].

Рассмотрим применение преобразования Лапласа на примере интегрирования одномерного уравнения пьезопроводности для плоскорадиального случая (1.4).

Перейдем в новые координаты и все формулы запишем относительно понижения давления (это делается для того, чтобы обнулить начальные условия (1.5)):

Из формулы (1.24) нетрудно получить важное свойство преобразования Лапласа:

Обширный обзор свойств преобразования Лапласа приведен в [12].

В результате применения преобразования Лапласа уравнение пьезопроводности

(1.25) перешло в обыкновенное дифференциальное уравнение, известное как модифицированное уравнение Бесселя:

Константы C1 и C2 находятся из граничных условий. При этом начальное условие было использовано при переходе в пространство Лапласа.

1.3.5. Исследование потенциальных течений с помощью методов функций теории комплексного переменного

Если характеристики фильтрационных потоков не меняются со временем

(стационарны), то распределение давления описывается уравнением Лапласа (которое получается из уравнения пьезопроводности, если предположить, что производная по времени равна нулю):

11

Контакты | https://new.guap.ru/i03/contacts

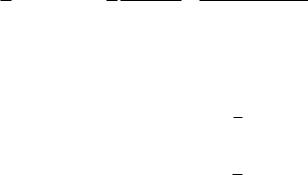
СПБГУАП| Институт 4 группа 4736

Такие режимы фильтрации называются установившимися. При двумерном

установившемся потоке в изотропных однородных коллекторах многие задачи фильтрации могут быть решены с помощью мощного математического аппарата комплексного анализа. Здесь мы не будем на этом останавливаться. Весьма подробно методы теории функций комплексного переменного (ТФКП) разобраны в [15]. В

приложениях к теории установившейся фильтрации также широкий круг задач (в том числе задачи площадного заводнения), с использованием методов ТФКП был решен Маскетом в его монографии [17]. Также полезно изучить по этой теме книги [16], [9].

1.3.6. Численные методы

Существует также численные методы решения уравнения пьезопроводности. Одни из широко применяемых – конечно-разностные методы. Суть метода заключается в следующем: пусть дана область, в которой хотим найти решение уравнения пьезопроводности. На границе этой области заданы граничные условия, например это могут быть условия: (1.6) – (1.11). В области задано начальное условие, например (1.5).

Область – пусть это будет интервал (a,b) – в одномерном случае, разбивается на J

отрезков, интервал времени, в котором ищется решение, – также разбивается на N

отрезков. Исходное уравнение заменяется при этом разностным уравнением, например:

Уравнение (1.29) получается из исходного – при использовании разложения функции в ряд Тейлора:

решением в этих узлах с некоторой погрешностью, которая зависит от величины шага по времени и мелкости разбиения данной области. Для того чтобы полученное решение было устойчивым, необходимо выполнение специальных условий, называемых критериями устойчивости, и вносящих ограничение на связь между шагом по времени и мелкости

12

Контакты | https://new.guap.ru/i03/contacts