Добавил:

spbguap9 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный минерально-сырьевой университет «Горный»

Предмет:

Добыча нефти и газа

Файл:

Математическое моделирование в процессах разработки и нефте-газодобычи

.pdf

Скачиваний:

Добавлен:

02.01.2021

Размер:

1.29 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

СПБГУАП| Институт 4 группа 4736

2.Математическая модель работы однопластовой скважины

2.1.Введение

Рассмотрим вертикальную скважину, работающую в центре однородного кругового пласта. Будем считать, что процесс фильтрации подчиняется закону Дарси, пласт является низкопродуктивным, так что режим течения длительное время остается неустановившимся. Пусть в начальный момент времени t =0 давление в любой точке пласта одинаково и равно pi .

Если скважина работает с постоянным дебитом или с постоянным забойным давлением, то зависимости соответственно забойного давления или дебита от времени могут быть найдены с использованием известных соотношений [6]. Кроме того,

существуют решения, позволяющие в рамках предположения о постоянстве дебита или забойного давления учесть эффект влияния ствола скважины.

В то же время, упомянутые выше решения не всегда адекватно отражают процессы,

происходящие при взаимной работе пласта и скважины. В действительности при движении многофазного потока по стволу скважины забойное давление определенным образом связано с дебитом, так что с течением времени ни один из этих параметров не остается постоянным. Указанная зависимость pwf pwf (Q) широко применяется при узловом анализе системы добычи [35] и может быть получена с помощью специальных методов расчета многофазного течения в трубах [26,27]. Результат такого расчета,

представленный в виде графика, носит название кривой эффективности лифта. Типичный вид этой кривой показан на рис.1.

Кривая эффективности лифта для механизированной скважины, оборудованной насосом (Рисунок 3.1b), может быть получена как разность между кривой эффективности лифта фонтанной скважины (Рисунок 3.1a) и напорной характеристикой используемого насоса.

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Рисунок 2.1. Графики зависимости забойного давления от дебита – кривой эффективности лифта для фонтанной (a) и механизированной (b) скважины

Характерной особенностью представленных кривых является наличие нисходящего и восходящего участков. При отсутствии потока (дебит равен нулю) свободный газ в столбе жидкости отсутствует, поэтому плотность смеси относительно велика и давление соответствует давлению статического столба. По мере увеличения дебита, из жидкости,

двигающейся в скважине, начинается выделяться газ, что приводит к уменьшению плотности смеси и уменьшению давления по сравнению с гидростатическим, что соответствует убывающему участку графика. При дальнейшем увеличении дебита скорость потока увеличивается, и все более сильное влияние оказывает сила трения,

которая приводит к дополнительным потерям давления по длине скважины, поэтому забойное давление начинает расти.

Таким образом, кривая эффективности лифта задает связь между дебитом и забойным давлением, и именно эта связь, а не предположение об их постоянстве, должна использоваться при описании реальных процессов, происходящих в системе пласт-

скважина. Исследование нестационарного притока из пласта в этом случае состоит в определении изменения дебита и забойного давления с течением времени с учетом указанной взаимосвязи. Сказанное проиллюстрировано на Рисунок 2.2 и Рисунок 2.3

Известные решения соответствуют кривым «Постоянное забойное давление» и «Постоянный дебит». Рассматриваемое ниже решение с учетом кривой эффективности лифта, при котором как дебит, так и забойное давление изменяются с течением времени,

соответствуют кривой «Рассматриваемый случай».

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Депрессия, P, атм

90 80 70 60 50 40 30 20 10 0

	1.1
	1.0
	0.9
D	0.8
p	0.8
,
давление	0.7
	0.7
	0.6
Безразмерное	0.5
Безразмерное	0.4					Постоянное забойное давление
						Постоянное забойное давление
						Постоянный дебит
						Постоянный дебит
	0.3					Рассматриваемый случай
	0.3
	0.2
	0.1
	0.0
	10	100	1000	10000	100000 1000000		1E7	1E8	1E9
				Безразмерное время, t			D
							D
		0.01	0.1	1	10	100	1000	10000	100000
				Время, t, сут

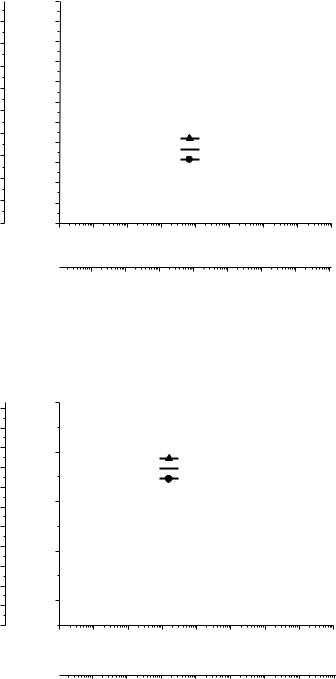
Рисунок 2.2. Зависимость забойного давления (депрессии) от времени в пласте с постоянным давлением на контуре при различных граничных условиях на скважине

Дебит, Q, м3/сут

	3.0
	2.5				Постоянное забойное давление
D					Постоянное забойное давление
D
Q					Постоянный дебит
,					Рассматриваемый случай
дебит	2.0
Безразмерный	1.5
	1.5
	1.0
	10	100	1000	10000	100000 1000000		1E7	1E8	1E9
				Безразмерное время, tD
		0.01	0.1	1	10	100	1000	10000	100000

Время, t, сут

Рисунок 2.3. Зависимость дебита от времени в пласте с постоянным давлением на контуре при различных граничных условиях на скважине

Численное решение задачи о взаимодействии пласта со скважиной во многих

случаях оказывается достаточно сложным и длительным и с трудом может быть

использовано для оперативных расчетов. Поэтому актуальным является построение

приближенных аналитических решений, позволяющих проводить быстрые оценки. Для

этого заметим, что во многих случаях в рабочем диапазоне дебитов возрастающий участок

кривой эффективности лифта с хорошей точностью можно аппроксимировать линейной

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

зависимостью забойного давления от дебита (показана на рис.1 пунктиром). Интересным с точки зрения практического приложения решения является именно возрастающий участок кривой эффективности лифта, так как он соответствует зоне устойчивой работы системы скважина-пласт, то есть практически все стабильно работающие скважины работают с

дебитами

Q Qc

. Убывающий участок соответствует прерывистой добыче,

неустойчивому потоку или заполнению жидкостью затрубного пространства [28,29].

Отметим, что при описании явлений, происходящих в стволе скважины,

используется кривая эффективности лифта, соответствующая стационарному подходу. С

другой стороны, при построении модели системы скважина-пласт в целом будет рассматриваться нестационарное решение. Правомерность такого подхода может быть проиллюстрирована на примере оценки характерных времен происходящих процессов.

Характерное время нестационарного перераспределения давления в пласте за счет

сжимаемости имеет порядок

t	2	/
t	~ L	/
1	1

, где

– коэффициент пьезопроводности,

L1	– характерный размер задачи по отношению к пласту. Характерное время

распространения возмущений в стволе скважины, заполненном многофазным флюидом,

определяет «время установления» кривой эффективности лифта и имеет порядок

t2 ~ L2 / u , где u – скорость всплытия пузырька газа, L2 – характерный размер задачи в
стволе скважины. Обычно	u – порядка 1 м/с,	L2 ~ 103 м, для низкопроницаемых
пластов ~ 10-2 10-1 м2/с, L1	~ 102 м. Поэтому t2 / t1	~ 10-2, откуда видно, что реакция ствола

скважины на изменение дебита происходит достаточно быстро по сравнению с реакцией пласта и может описываться единственной кривой в течение всего процесса фильтрации.

2.2. Построение модели с использованием преобразования Лапласа

Нахождение динамики дебита и давления для задач теории упругого режима фильтрации связано с решением уравнения пьезопроводности, которое в случае плоскорадиальной симметрии имеет вид:

	2	p	1 p	1 p
	2
r		2	r r	t	,	r 0,	t 0,
r			r r	t

где p p(r,t) – давление в пласте.

Запишем начальное условие:

(2.1)

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

1 p

r r

r 0,

t 0,

(2.2)

Как уже отмечалось, в качестве граничных условий на скважине, моделирующих

условия ее работы, в основном используют следующие предположения:

p(r,t)

r r

const

– для скважин с постоянным забойным давлением;

Q(r,t)

r r

Qsf

const

– для скважин с постоянным дебитом;

Qsf Bl	Qwh Bl	Cs	p	,	Qwh const
Qsf Bl	Qwh Bl	Cs	t	,	Qwh const
			t	r r
				w

– для учета влияния ствола скважины.

Здесь Cs – коэффициент влияния ствола скважины, влияние которого на процесс добычи будет рассмотрено ниже, Qwh – дебит жидкости на поверхности, Qsf – дебит пластовой жидкости на забое скважины, определяемый из закона Дарси:

Q	r,t		2 kh	r	p
Q	r,t			r
sf			B
		r r	B		r
		w	l
			l

r rw

(2.3)

В работе рассматривается решение для другого вида граничных условий,

определяемых видом кривой эффективности лифта с учетом ее линейной аппроксимации:

p(r,t)	r rw	aQ	p	(2.4)

		wh	0

где a , p0 – некоторые константы, определяемые из условия наилучшего совмещения прямой и кривой эффективности лифта в рабочем диапазоне.

Если эффект влияния ствола скважины не учитывается, то дебит на поверхности равен дебиту из пласта ( Qsf Qwh ), поэтому с учетом выражения (2.3) граничное условие

(2.4) является граничным условием третьего рода, которое описывает совместную работу

пласта и скважины.

Различные виды внешних граничных условий, зависящие от типа рассматриваемого

пласта, запишем в виде:
p	r		p		,	t 0,	(2.5)
	r			i
p	r re		p	,		t 0,	(2.6)
	r re		i				(2.6)
			i
p			0,			t 0.
r			0,			t 0.
r		r r					(2.7)
		r r					(2.7)
			e

Граничное условие (2.5) соответствует случаю плоскорадиального притока жидкости

к скважине из бесконечного по протяженности пласта с «условием на бесконечности» в

виде давления, равного начальному пластовому давлению pi . Условия (2.6) и (2.7)

соответствуют случаям, когда внешняя граница кругового пласта радиусом re является

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

либо контуром питания, на котором поддерживается постоянное пластовое давление		pi ,
либо замкнутой границей, через которую невозможен переток жидкости.
Заметим, что если значение скин-фактора S 0 ,	то в качестве радиуса скважины
можно использовать эффективный радиус скважины r	r e S .
w	w

Решая уравнение (2.1) с начальным условием (2.2) и граничными условиями, (2.4)- (2.7), требуется определить давление p и расход Q в скважине в любой момент времени

t 0.

Для упрощения решения введем в

рассмотрение величину понижения давления

(депрессию):

P(r,t) pi

p(r,t) .

(2.8)

При замене величины

на P

уравнение пьезопроводности (2.1) сохранит свой вид.

Перейдем к безразмерным переменным:

2a kh

Тогда с учетом выражения (2.3) запишем уравнение пьезопроводности, а также

начальное и граничные условия в виде:

1 p

(2.9)

при

(2.10)

при

(2.11)

при

(2.12)

В последующем изложении для определенности,

но без ограничения общности,

будем рассматривать внешнее граничное условие, соответствующее бесконечному пласту.

Граничные условия в безразмерном виде для других случаев задания внешней границы пласта приведены в Таблице 1.

Решение задачи (2.9)-(2.12) будем искать с использованием методов операционного исчисления. Применим к уравнению и граничным условиям преобразование Лапласа.

Преобразование Лапласа [30] связывает оригинал искомой функции с ее изображением

следующим интегральным соотношением:


	~	r, s		e	st	pD r,t dt ,
	pD	r, s		e		pD r,t dt ,
			0
~	r, s – изображение	функции,				pD r,t – оригинал, s – параметр
где pD	r, s – изображение	функции,				pD r,t – оригинал, s – параметр

преобразования. Следуя правилам операционного исчисления [30] и учитывая начальное условие (2.10), правая часть уравнения (2.9) в пространстве Лапласа примет вид:

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

~
p	D

t

~		p		(t
sp	D		D		D

~
sp	D
	D

Тогда задачу (2.9)-(2.12) в пространстве Лапласа можно записать в следующем виде:

при rD 1,

tD 0,

rD r

pD 0

при rD ,

tD 0.

(2.13)

(2.14)

Для других видов внешних граничных условий формулы приведены в таблице 1.

Тип пласта

Круговой пласт с постоянным давлением на контуре

Круговой пласт с непроницаемой границей

Таблица 1

Граничные условия в обычном

Граничные условия в

пространстве

пространстве Лапласа

при r

r , t

при

По изображению безразмерного давления, используя выражение (2.3), найдем

изображение дебита скважины:

, s)

(2.15)

где QD

Q(r,t) r rw Bl

– безразмерный дебит скважины.

2 kh( pi p0 )

В результате применения операционного метода задача об интегрировании

дифференциального уравнения

с частными производными (2.1) сведена к более простой

задаче интегрирования обыкновенного дифференциального уравнения (2.13). Уравнение

(2.13) является модифицированным дифференциальным уравнением Бесселя. Его общее решение можно записать в виде [31]:

0 D

(r , s)

(2.16)

где

I 0 и

K 0 – модифицированные функции Бесселя нулевого порядка I и II рода,

которые

могут

быть вычислены

использованием

любого математического пакета

(включая MS Excel). A и B – постоянные коэффициенты, определяемые из граничных условий (2.14)-(2.15).

Решение задачи (2.9)-(2.12) в пространстве Лапласа выглядит следующим образом:

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

s )

(2.17)

, s)

s K

( s ) C

(

s )

1, s)

s K

s )

(2.18)

(

s ) C

(

Для других граничных условий общий вид решения в пространстве Лапласа

приведен в таблице 2

Таблица 2

s )I

s ) I

s )K

s )

s C

s )

Круговой

s K (

s )I

s ) I (

s )K

s )

(

s )I

s ) I

(

s )K

пласт с

постоянным

K (

s)I

s) I (

s)K

давлением

s C s

K (

s) K

на контуре

s)I

s) I (

s)K

(

s)I

s) I

(

s)K

Круговой

s )I (r

s ) I

s )K (r

s )

пласт с

s C

s K ( s )I (r

s ) I (

s )K (r

s ) K

(

s )I (r

s ) I

(

s )K (r

s )

непроницае

мой

K (

s )I (r

s ) I (

s )K (r

s )

границей

s C

s K (

s )I (r

s ) I (

s )K (r

s )

(

s )I (r

s ) I

(

s )K (r

s )

После того, как определены изображения искомых функций, необходимо вернуться в обычное пространство. Для этого нужно произвести обратное преобразование Лапласа.

Для перехода к оригиналу воспользуемся численным алгоритмом [32], по которому осуществляется обратное преобразование Лапласа при заданных значениях безразмерного времени tD.

Таким образом при заданных граничных условиях определим забойное давление и дебит скважины как функцию времени.

2.3.Решение с учетом влияния объема ствола скважины

В рамках операционного метода Лапласа можно получить точное решение рассматриваемой задачи с учетом влияния объема ствола скважины. Как уже отмечалось,

для этого запишем граничное условие на скважине в виде [34]:

Qsf Bl Qwh Bl	Cs	p	.	(2.19)
		t	r r
			w
Заметим, что в отличие от ранее рассматриваемых случаев Qwh				теперь не является

постоянной величиной, а должен определяется из условий работы скважины, то есть из выражения (2.2):

Qwh	p(r,t)	r rw	p0	.	(2.20)
		r rw
		a
		a
			30

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

В остальном ход решения аналогичен представленному ранее. Решение в

пространстве Лапласа для бесконечного пласта выглядит следующим образом:

s )

(2.21)

, s)

s K

s )

(

s ) 1 CC

s C

(

1, s)

s K

s )

(2.22)

( s ) 1 CC

(

где CD

– безразмерный коэффициент влияния ствола скважины.

r 2

2 hc

Для других случаев задания внешних граничных условий решения показаны в

таблице 3.

Таблица 3

Круговой

(rD

s )I0

(reD s ) I0

(rD

s )K0 (reD

s )

пласт с

s C s K ( s )I

s ) I (

s )K

s )

1 CC

s K

(

s )I

s ) I

(

s )K

s )

постоянн

ым

давление

K (

s )I

s ) I ( s )K

s )

м на

s K (

s )I

s ) I (

s )K

s ) 1 CC

s K

(

s )I

s ) I

(

s )K

s )

контуре

K0 (rD s )I1(reD s ) I0 (rD s )K1(reD s )

Круговой

s C

s )K1(reD s )

s K1(

s )I1(reD

s ) I1(

s )K1(reD

s ) 1 CCD s K0 (

s )I1(reD

s ) I0 (

пласт с

непрониц

аемой

K (

s )I (r

s ) I ( s )K (r

s )

1 eD

границей

s C

s K ( s )I (r

s ) I (

s )K (r

s ) 1 CC

s K

(

s )I (r

s ) I

(

s )K (r

s )

Следует отметить, что решение с учетом влияния ствола скважины получено при

условии стационарности кривой эффективности лифта, которое, строго говоря, будет

справедливо лишь по прошествии некоторого характерного времени t2

с момента начала

работы скважины. Характерное время эффекта влияния ствола скважины имеет порядок

			V
t		~		an
t	3	~	Q
	3
				pump
				pump

, где

V	an

– объем затрубного пространства, а

Q	pump

– производительность насоса.

Обычно Van – порядка 10 м3, Qpump ~ 10 3 м3/с. Используя проведенную выше оценку

значения времени t2 , получим

t	3

t	2

, откуда видно, что эффект влияния ствола

скважины значительно более медленный процесс, чем процесс «установления» кривой лифта, а, значит, может рассматриваться в рамках предложенной математической модели.

2.4.Анализ результатов

Контакты | https://new.guap.ru/i03/contacts

СПБГУАП| Институт 4 группа 4736

Полученное решение, а также известные решения для случая задания на скважине постоянного давления или дебита представлены на рис.2. В данном примере a = 2.12

атм/(м3/сут) , p0 = 50 атм, pi = 250 атм, re = 200 м, rw = 0.1 м, h = 10 м, = 0.001 м2/с.

Рассматривается пласт с постоянным давлением на контуре, эффект влияния ствола скважины не учитывается.

Как видно из графиков в отличие от известных решений в случае учета работы системы пласт-скважина в целом (при задании на скважине кривой эффективности лифта в линейной аппроксимации) как забойное давление, так и дебит изменяются с течением времени. Это продолжается до тех пор, пока влияние границ невелико. После этого распределение давления устанавливается, дебит становится постоянным, и работа скважины переходит в стадию установившегося режима.

Кривые, описывающие изменение дебита скважины и забойного давления при различных вариантах задания внешних граничных условий и с учетом влияния ствола скважины (Cs = 0.01 м3/атм) показаны Рисунок 2.4 - Рисунок 2.5. Пунктиром показаны результаты расчета без учета влияния ствола скважины. Представленные зависимости отражают процессы, происходящие в пласте и скважине при их совместной работе.

В начальные моменты времени ( t t* ) определяющую роль в изменении забойного давления и дебита играет эффект влияния ствола скважины. Дебит из пласта непосредственно после запуска скважины практически равен нулю. При этом добыча на поверхности идет в основном за счет жидкости, находящейся в затрубном пространстве. В

дальнейшем все больше пластового флюида поступает на поверхность, уровень столба жидкости в затрубном пространстве стабилизируется, и после окончания периода влияния объема ствола скважины пластовый и поверхностный дебиты становятся равными.

Отметим, что в реальной практике нефтедобычи эффект влияния ствола скважины не играет большой роли из-за своей непродолжительности, но должен учитываться при проведении гидродинамических исследований скважин [33].

В дальнейшем, при t* t t** и давление, и дебит, изменяясь с течением времени,

определяются нестационарным процессом распространения возмущения давления в пласте. Заметим, что во время неустановившегося режима (на графиках это соответствует временам t t** ), когда скважина еще «не чувствует» внешних границ на характер изменения забойного давления и дебита не влияет тип пласта (вид внешних граничных условий), поэтому кривые во всех трех случаях совпадают.

Контакты | https://new.guap.ru/i03/contacts

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете Добыча нефти и газа

#
17.01.2021187.96 Кб22Малоглубинная сейсморазведка.pdf
#
14.02.2021793.46 Кб30Маркетинг Татнефть.pdf
#
01.02.20211.25 Mб6Массовые кориолисовые расходомеры и плотномеры.pdf
#
17.01.2021394.03 Кб16мат. моделирование сейсморазведка.pdf
#
02.01.20214.66 Mб86МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ НЕФТЕГАЗОВОЙ ОТРАСЛИ.pdf
#
02.01.20211.29 Mб54Математическое моделирование в процессах разработки и нефте-газодобычи.pdf
#
03.02.20211.69 Mб6Мембранные технологии в установках получения азота из воздуха.pdf
#
21.01.20213.93 Mб68Мероприятия по интенсификации добычи нефти на Мишкинском нефтяном месторождении».pdf
#
03.02.20211.63 Mб2МЕСТОРОЖДЕНИЯ МАГНИТОГОРСКОЙ МЕГАЗОНЫ.pdf
#
06.01.2021319.64 Кб1Месторождения подземных вод.pdf
#
31.01.20211.35 Mб2метод анализа нефти и нефтепродуктов.pdf