Здоровцева Г.Г. Контролируемая самостоятельная работа студентов по курсу «Общая физика». Тема «Механика точки»

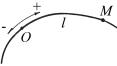
1. КИНЕМАТИКА ТОЧКИ

Кинематика – раздел механики, посвященный изучению геометрических свойств движения тел без учета их масс и действующих на них сил.

Движением точки считается заданным, если известен способ, которым можно определить положение точки в любой момент времени относительно выбранной системы отсчета. Существует три взаимосвязанных способа описания движения.

Векторный способ. Движение точки в пространстве будет вполне определено, если известен ее радиус-вектор r как функция времени

Координатный способ. Движение точки по отношению к ка- кой-нибудь системе координат полностью определено, если известно, как изменяются координаты точки со временем.

Если движение рассматривается в декартовой прямоугольной системе координат, то задаются координаты точки x, y, z как известные функции времен, то есть

Естественный способ. Используется, когда известна траектория движения точки М (рис. 1.1). На траектории выбирается какаянибудь неподвижная точка О, которую принимают за начало отсчета. Устанавливается положительное и отрицательное направле-

Закон движения точки вдоль траектории задается уравнением

При естественном способе описания движения для определения проекций векторных величин относительно траектории вводятся

единичные векторы – орты (τ, n, b) , направленные следующим образом:

4

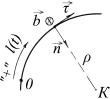
τ (тангенциаль) – вдоль касательной к траектории, в сторону положительного отсчета расстояния l;

n (нормаль) – к центру кривизны траектории;

и b образовали бы правую тройку векторов (рис. 1.2). Указанные выше оси называются осями

естественного (или сопровождающего) трехгранника, так как обозначаемые ими направления существуют в любой точке траектории, как бы сопровождая точку при ее движении.

На примерах решения задач, которые будут рассмотрены ниже, убедимся, что если закон

движения точки задан, то все ее кинематические характеристики (перемещение, скорость, ускорение, траектория, путь) могут быть определены.

Приступая к решению задач необходимо:

Проработать теоретический материал по теме «Кинематика точки» по учебным пособиям из списка рекомендуемой литературы.

Ответить на вопросы:

1. Что является предметом изучения кинематики?

2. Что понимается под движением в механике?

3. Когда движущееся тело можно считать материальной точкой? 4. Какие способы задания движения известны? В чем их суть? 5. Дать определения радиуса-вектора точки, перемещения, ско-

рости, ускорения, траектории, пути.

6. Как найти перечисленные выше кинематические характеристики движения по заданным в декартовой системе координат уравнениям движения (1.2)?

7. Как найти все перечисленные в п.5 кинематические характеристики, если закон задан в векторном виде (1.1)? Как связан ра- диус-вектор точки с ее декартовыми координатами?

8. Что такое естественный трехгранник? Как направлены орты

(τ,n,b) относительно траектории движения точки? С чем связано направление упомянутых векторов?

9. Дать определение тангенциальному и нормальному ускорениям. Как их найти, если движение задано координатным способом или векторным способом?

5

10. Как по заданным в декартовой системе координат проекциям ускорений, начальному положению точки и её начальной скорости определить все остальные кинематические характеристики, перечисленные в п.5?

Примеры решения задач

Задача 1.1. Радиус-вектор точки A относительно начала коорди-

стоянные, i и j – орты осей x и y. Найти: а) уравнение траектории точки y(x), б) зависимость от времени скорости, ускорения и модулей этих величин, в) зависимость от времени угла ϕ между скоростью и ускорением.

Решение.

а) Уравнение движения точки А задано векторными способом. Для нахождения траектории необходимо знать, как меняются со временем координаты x(t) и y(t).

Выражая радиус-вектор через его проекции на оси координат

и сопоставляя (1) с заданным в условии задачи уравнением движения r = r (t) , заключаем

Чтобы получить уравнение траектории y = y(x), надо из уравнений (2) исключить время t. Используем метод подстановки. Выразим время t через координату x:

Уравнение траектории (3) получено. Это парабола с вершиной в

dt

6

Модуль скорости находим как квадратный корень из суммы

в) Угол между скоростью и ускорением проще всего, на наш взгляд, найти, если воспользоваться двумя способами раскрытия скалярного произведения векторов:

(ab) = abcosϕ = axbx + ayby ,

где a и b – любые два вектора, ϕ – угол между ними, ax и bx – проекции этих векторов на ось x; ay и by – проекции на ось y.

Резюме. Точка начинает двигаться из начало координат r(0) = 0

С течением времени угол ϕ между вектором скорости v , который направлен по касательной к траектории точки в сторону ее движения, и вектором ускорения a уменьшается, стремясь к нулю (по уравнению (8) cosϕ → 1 при t → ∞).

Итак, движение полностью описано.

траекторию, скорость, ускорение точки.

Решение. Движение точки задано координатным способом. Как и в предыдущей задаче, надо найти все основные кинематические характеристики. Чтобы найти уравнение траектории из кинематических уравнений движения исключаем время t.

7

Выразим t через х:

t = x ,

ленной под углом ϕ = arctg c к горизонтали, и дальше двигалась a

по ветви параболы с возрастающей по абсолютной величине скоростью. Модуль скорости v = a2 + (c + 2bt)2 .

Со временем угол ϕ между вектором скорости v и горизонталью увеличивается за счёт роста вертикальной составляющей скорости vy . Вдоль оси х проекция скорости vx остается постоянной.

Соответственно, наклон вектора скорости (наклон касательной) к оси x линейно возрастает с течением времени

tgα = vy = 2bt + c . vx a

Задача 1.3. Точка движется по окружности радиуса R по закону

l = v0t − 1 at2 . Найти скорость и ускорение точки.

2

8

Решение. Траектория точки известна. Движение задано естественным способом. l – длина, отсчитываемая от некоторой точки О на траектории: «криволинейная координата».

Вектор скорости направлен по касательной к траектории в каждой ее точке, поэтому его можно представить как

Дифференцируем заданное уравнение движения точки – «криволинейную координату» – по времени и записываем вектор скорости

Из уравнения (2) проекция вектора скорости точки на тангенциаль vτ = (v0 − at) , а модуль скорости v = vτ = v0 −at .

Полное ускорение точки находим как сумму тангенциального и

нормального ускорений, т.е. как сумму его составляющих по направлениям τ и n :

ускорения на нормаль n .

Выполним преобразования и выразим проекции полного уско-

Модуль полного ускорения находится по теореме Пифагора:

Резюме. Материальная точка начинает (t = 0) свое движение из некоторой точки О на окружности, принятой за начало отсчёта, с начальной скоростью v(0) = v0. Поскольку aτ < 0, то материальная точка замедляет свое движение. В момент времени t =v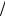a точка останавливается (v(t) = 0) и затем продолжает движение уже в об-

9

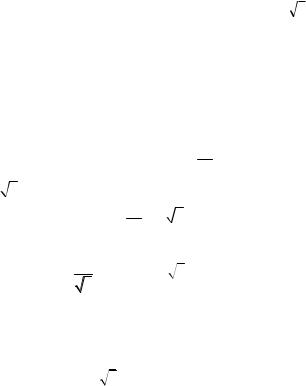
ратном направлении (vτ = (v0 − at) < 0) с возрастающей по модулю скоростью.

Задача 1.4. Точка движется по дуге окружности радиуса R. Ее скорость зависит от пройденного пути s по закону v = αs , где α – постоянная. Найти угол ϕ между вектором полного ускорения a и вектором скорости v в зависимости от S.

Решение. Задача отличается нестандартной постановкой: уравнение движения не задано, его надо найти.

Поскольку известна траектория (окружность), то целесообразно описывать движение «естественным» способом. Найдём уравнение движения точки вдоль дуги окружности s = s(t).

Модуль скорости по определению v = ds . Он же по условию за- dt

дачи v = α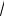s . Составим уравнение:

ds = αs . dt

Решаем это уравнение – разделяем переменные и интегрируем: ∫ dss = ∫αdt, 2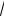s = αt + const.

Используем начальные условия для нахождения константы интегрирования. Поскольку длина дуги (путь) отсчитывается с момента начала движения, т.е. при t = 0, s = 0, получаем const = 0. То-

гда

2s = αt или s = α2 t . (1) 4

Уравнение движения точки получено.

Найдём ϕ. Вектор скорости направлен по касательной к траектории, поэтому искомый угол ϕ будет углом между векторами полного ускорения a и тангенциальной составляющей ускорения aτ :

10