
3-й семестр / Лекции / 07 - презентация
.pdf
Пример 3. Разложить в ряд Маклорена функцию:
1( ) = 2−3 +2.
Разложим дробь на сумму простейших дробей, и к каждой из них применим табличное разложение в ряд Маклорена:
1 |
|
= |
|
|
1 |
= |
|
|
1 |
− |
1 |
= |
1 |
|
− |
1 |
= |
1 |
− |
1 |
∙ |
1 |
|
= |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2−3 +2 |
( −1)( −2) |
|
−2 |
−1 |
1− |
|
2− |
1− |
2 |
1− |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
= ∑∞=0 − |
1 |
∙ ∑∞=0 |
|
|
= |
∑∞=0 (1 − |
|
|
1 |
) . |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
+1 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
2 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Для нахождения области сходимости решим систему неравенств:
−1 < < 1 |
−1 < < 1 |
|
|||
|
|
|
|
||
{−1 < |
|
< 1 {−2 < < 2 |
−1 < < 1. |
||
2 |
|||||
|
|
|
|
||
Пример 4. Разложить в ряд Тейлора функцию |
|
||||||
( |
) |
= ln( |
2 |
+ 5 + 6) в окрестности точки ( 0 |
= −1), т.е. по |
||
|
|
|
|||||
степеням ( + 1). |
|
|
|
||||
Сделаем |
замену: |
+ 1 = |
и, пользуясь свойствами |
||||
логарифмической |
функции, |
выполним |
тождественные |
||||
преобразования: |
|
|
|
||||
( ) = (( − 1)2 + 5( − 1) + 6) = ln( 2 + 3 + 2) = = ln(( + 1)( + 2)) = ln( + 1) + ln( + 2) =
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
+ ∑∞=1(−1) −1 |
∙ |
|
+ ∑∞=1(−1) −1 |
∙ |
|
= |
||||
|
2 ∙ |
||||||||||
= 2 |
+ ∑∞=1 |
(−1)−1 |
∙ (1 + |
1 |
) . |
|
|
|
|||
|
2 |
|
|
|
|||||||
Вернемся к исходной переменной:
( ) = 2 + ∑∞=1 |
(−1)−1 |
1 |
) ( + 1) . |
||||
|
∙ (1 + |
|
|||||
|
2 |
||||||
|
−1 < < 1 |
|
|
||||
Область сходимости: {−1 < |
|
< 1 |
|
−1 < < 1 −1 < + |
|||
|
|
|
|||||
|
|
2 |
|
|
|
||
1 < 1 −2 < < 0.
Пример 5. Разложить в ряд Тейлора функцию ( ) = ( + 2) ∙ 3 в окрестности точки ( 0 = −2), т.е. по степеням ( + 2).
Сделаем замену: + 2 = , = − 2:
( ) |
|
−2 |
|
|
|
1 |
|
|
|
1 |
3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
= ∙ 3 |
|
= |
9 |
∙ 3 = |
9 |
∙ |
|
|
= |
||||||||
= |
1 |
∙ 3 |
= |
1 |
∙ ∑=0∞ |
|
|
3. |
|
|
|
|||||||
|
|
|
|
|||||||||||||||
|
9 |
|
! |
|
|
|
||||||||||||
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вернемся к исходной переменной:
( |
) |
|
∑∞ |
3 |
+1 |
|
|
|
= |
=0 |
|
|
( + 2) . |
|
9 ! |
|||||
|
|
|
|
|
||
Область сходимости: (−∞, +∞).

Пример 6. Разложить функцию = sin2 в ряд Маклорена.
Воспользуемся тригонометрическим тождеством:
sin2 = 12 (1 − cos2 ) ,
а затем табличным разложением функции cos , заменяя переменную на переменную 2 :
sin2 = |
1 |
|
− |
1 |
(1 − |
(2 )2 |
+ |
|
(2 )4 |
|||
2 |
|
2! |
4! |
|||||||||
|
|
|
|
|
|
2 |
|
|||||
2 2 |
|
23 |
|
4 |
|
|
|
+1 |
||||
|
|
|
|
|
|
|
|
|
( |
|
) |
|
= 2! − |
|
|
|
|
|
|
||||||
|
4! + + −1 |
|
|
|||||||||
(−∞, +∞).
− + (−1) (2 )2 + ) =
(2 )!
22 −1 2 + ,
(2 )!
6.5.2. Использование почленного интегрирования
Пример 7. Разложить в ряд Маклорена функцию ( ) = .
Воспользуемся табличным разложением для представления степенным рядом производной этой функции:
′ |
|
( |
|
|
|
|
)′ |
|
1 |
|
|
2 |
|
4 |
( |
) |
|
2 |
|
||||
|
( ) = |
|
|
|
= |
1+ 2 |
= 1 − |
|
+ |
|
|
− + −1 |
|
∙ |
|
+ , |
|||||||
(−1,1). |
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= ∫0 |
|
1 |
|
= ∫0 (1 − 2 |
+ 4 − + (−1) ∙ 2 + |
|
|||||||||||||||||
|
1+ |
2 |
|
||||||||||||||||||||
|
) |
|
|
3 |
|
|
|
5 |
|
|
( ) |
|
|
2 +1 |
|
|
|
|
|
||||
|
|
= − |
|
3 |
+ |
|
5 |
− + −1 |
|
∙ |
2 +1 |
+ , [−1,1]. |
|
||||||||||
Заметим, что производная представляется степенным рядом на интервале (−1,1), а сама функция – на отрезке [−1,1].

6.5.3. Использование почленного дифференцирования Пример 8. Разложить в ряд Тейлора функцию
( ) = |
5 |
|
|
, 0 = 2. |
|
Замена: − 2 = , = + 2. |
||||||||||||||||||||||
( +1) |
2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
|
||
( ) |
|
|
|
5 |
|
|
|
|
|
|
|
|
1 |
|
|
5 |
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
= 5 ∙ − ( |
|
) = − |
|
|
|
∙ ( |
|
) = |
|
|
||||||||||||||
|
( +3)2 |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
+3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
|
∙ (∑∞=0(−1) |
|
′ |
5 |
|
∑∞=0(−1) |
|
−1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
= − |
|
|
|
|
) = − |
|
∙ |
|
|
= |
||||||||||||||||||
3 |
|
3 |
3 |
|
3 |
|||||||||||||||||||||||
∞ |
|
|
+1 |
5 |
|
|
|
|
|
−1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
= ∑ =0(−1) |
|
|
|
( − 2) |
. |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
3+1 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Область сходимости: −1 < 3 < 1 −3 < < 3
−3 < − 2 < 3 −1 < < 5.

6.6.Применение теории степенных рядов
6.6.1.Приближенные вычисления значений функций
Рассмотрим примеры применения ряда Тейлора для приближенных вычислений.
Пример 9. Вычислить sin1 с точностью до 0,001.
Для решения задачи воспользуемся табличным разложением функции sin :
sin1 = 1 − 13 + 15 − 17 + - знакочередующийся ряд Лейбница.
3! 5! 7!
При замене суммы ряда на частичную сумму остаток не превосходит по модулю первого отброшенного члена ряда.
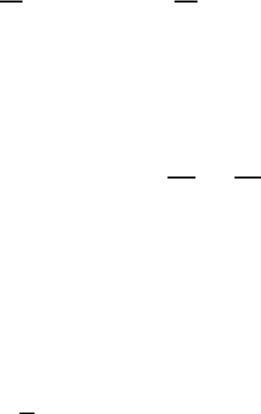
5!1 > 0,001, 7!1 < 0,001, значит, это слагаемое можно отбросить,
для достижения заданной точности достаточно учесть первые три члена ряда:
sin1 ≈ 1 − 13 + 15 = 0, 842.
3! 5!
6.6.2. Приближенные вычисления определенных интегралов
Пример 10. Вычислить с точностью до 3 знаков после запятой
1
∫04 − 2 .
Воспользуемся разложением функции в ряд Маклорена, заменив в нем на − 2:

− 2 = 1 − |
2 |
+ |
|
4 |
|
− |
6 |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
2! |
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
1! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
4 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
∫04 |
− 2 = ∫04 |
(1 − |
|
|
+ |
|
− |
|
|
+ ) = |
|
|
|
|
|
|
|
||||||||||||||||||
1! |
2! |
3! |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
5 |
|
|
|
|
|
7 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
||||||||
= ( − |
|
+ |
|
|
|
− |
|
|
+ )| = |
|
− |
+ |
|
− |
|
+ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
5 |
42 ∙ 4 |
7 |
|||||||||||||||||||||
3 |
10 42 |
|
|
0 |
|
4 |
3 ∙ 4 |
10 ∙ 4 |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получен |
знакочередующийся |
ряд |
Лейбница, |
слагаемое |
1 |
||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||
|
10∙45 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньше, чем 0,001. Отбрасывая это слагаемое, получим приближенное значение интеграла с заданной точностью:
1
∫04 − 2 ≈ 14 − 3∙41 3 = 0,245.
