16.Гидравлические потери по длине трубопровода. Вывод уравнения дАрсиВейсбеха . Коэф гидравлического трения

17.Графики Никурадзе. Абсолютная и относительная шероховатость труб. Понятия гидравлических гладких и шереховатых труб

Абсолютной шероховатостью k называют среднюю высоту выступов шероховатости. Относительной шероховатостью называется отношение абсолютной шероховатости к диаметру трубы. 1) Гидравлически гладкие трубы -   , т.е. толщина ламинарного слоя больше высоты выступов шероховатости. В этом случае шероховатость стенок не влияет на характер движения и соответственно потери напора не зависят от шероховатости. 2)Гидравлически шероховатые трубы -   , т.е. толщина ламинарного слоя меньше высоты выступов шероховатости. В этом случае шероховатость стенок влияет на характер движения и соответственно потери напора зависят от шероховатости.

18.Понятие местного сопративления . Основные виды местных сопративлений . Расчетпотерь напора на их преодаление .Эквивалентная длина местных сопративлений Местные сопротивления При движении реальных жидкостей кроме потерь на трение по длине трубопровода, возникающих из-за вязкости жидкости, могут возникать потери напора, связанные с наличием местных сопротивлений (краны, задвижки, сужения, расширения, повороты трубопроводов и проч.), которые вызывают изменения скорости движения или направления потока. Потери напора в местных сопротивлениях определяются по формуле

 

Виды Вход в трубу, внезапное расширение трубы, постепенное расширение, внезапное сужение трубы, постепенное сжатие трубы, выход из трубы, резкий поворот( колено), диафрагма , задвижка

19) Внезапное расширение потока. Расчет потерь напора (уравнение Борда)

При внезапном расширении потока в трубопроводе от площади S₁ до S₂ (рис. 7.4), жидкость не растекается по контуру излома стенок, а следует по более плавным линиям тока. Около стенок образуется пространство, в котором жидкость находится во вращательном движении. Потеря напора, происходящая при внезапном расширении потока реальной жидкости, находится с помощью уравнения Д. Бернулли, записанного для сечений 1-1 и 2-2, где движение считается плавно изменяющимся. Тогда:

(7.7) Применяя теорему о количестве движения и произведя необходимые преобразования, выражаем h_в.р через средние скорости

Называя разность (₁ – ₂) потерянной скоростью следует, что потеря напора при внезапном расширении равна скоростному напору, подсчитанному по потерянной скорости (теорема Борда). Зависимость (7.6) записывается в виде

или

С учетом того, что по уравнению неразрывности ₁s₁=₂s₂, из (7.7) получим

, (7.8) где ; Для некоторых видов сопротивлений таких как внезапное расширение или сжатие потока и их частные случаи: вход и выход из трубы значения коэффициента местного сопротивления возможно определить по уравнению Бóрда:

(6.11)

где и – скорости до и после внезапного расширения, м/с.

В формулу (6.11) входят величины средних скоростей течения υ₁и υ₂ , связанные между собой уравнением неразрывности . Заменив и вынеся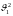 за скобку, приведем формулу к виду:

, где (6.12)

Аналогично, вынося за скобки , получим

, где (6.13)

Коэффициенты ζ_вр и называются коэффициентами сопротивления при внезапном (резком) расширении потока.

В частном случае, когда S₂>>S₁, т.е. имеет место расширение потока при выходе из трубы в резервуар больших размеров, получается так называемая потеря напора «на выходе из трубы».ζ_вых здесь в соответствии с формулой (6.11) получаем ζ_вых=1,0, а следовательно потеря напора на выходе из трубы будет определяться по уравнению:

При проведении гидравлических расчетов часто на расчетном участке трубопровода встречаются несколько видов местных сопротивлений либо несколько сопротивлений одного вида. В этом случае гидравлические потери при прохождении потоком таких участков могут быть определены по выражению: , (6.15) где n и ζ – число и коэффициент сопротивления данного вида местного сопротивления.

Иногда при расчете трубопроводов (особенно при определении их напорных характеристик) сумму коэффициентов местных сопротивлений заменяют эквивалентной длиной трубопровода l_э. Эта величина представляет собой длину простого трубопровода величина гидравлических потерь которого равна величине потерь на преодоление местных сопротивлений. Она может быть определена из сопоставления уравнений (6.2) и (6.15), т.е.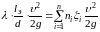

Откуда . (6.17)

Уравнение (6.1) для определения общих гидравлических потерь может быть преобразовано к виду:

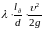= (6.18)

где l + l_э = l_р – расчетная длина трубопровода, м.

20) Классификация трубопроводов. Расчет диаметра трубопровода. Понятие экономичной скорости. Классификация трубопроводов Трубопроводами называют устройство, выполняемое из труб и других стандартных изделий (комплектующих), предназначенное для перемещения и транспортировки подвижных сред. В зависимости от назначения и рода перемещаемой среды различают: технологические трубопроводы, водопроводы, нефтепроводы, газопроводы, воздухопроводы и т. п. Если движение жидкости происходит за счет разности ее геометрических высот в начале и в конце трубопровода, то такое течение называется самотечным, а трубопровод–безнапорным. Отличительным признаком безнапорного движения жидкости является наличие свободной поверхности, а давление в потоке равно атмосферному. Движение жидкости в напорных трубопроводах происходит благодаря разности давлений (напоров) в начальном и конечном их сечениях. Эта разность давлений может быть создана при помощи насоса либо за счет уровня жидкости, либо под действием газа в резервуаре, из которого движется жидкость. При этом жидкость полностью заполняет все сечение трубопровода, а давление в трубопроводе выше атмосферного. Все трубопроводы делятся на простые и сложные; длинные и короткие. К простым относят трубопроводы постоянного диаметра. Короткими считаются трубопроводы сравнительно небольшой длины, в которых местные потери напора составляют не менее 5 – 10 % потерь напора на трение по длине. При их расчете исходят из принципа наложения потерь и принимая

Длинные–это трубопроводы значительной протяженности, в которых потери на преодоление местных сопротивлений составляют не более 5 – 10 % потерь напора по длине. При расчете их вовсе не учитывают, либо учитывают увеличение потерь напора на трение по длине на 5 – 10 %, т.е. Все сложные трубопроводы выполняются, как правило, комбинированием из простых. Их основные виды приведены в классификации на рисунке 2.1.

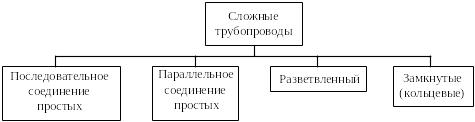
Рисунок 2.1– Классификация трубопроводов

Расчет диаметра трубопровода Как известно, к простым трубопроводам относятся трубопроводы произвольной конфигурации с запорно–регулирующей арматурой постоянного диаметра. Такой трубопровод имеет среднюю скорость потока постоянную на всем своем протяжении. Т.е. скорость в начале трубопровода равна скорости потока в конце трубопровода, а следовательно, и скоростные напоры в рассматриваемых сечениях будут одинаковы, а именно .

При расчете такого трубопровода на первом этапе возникает необходимость в расчете его диаметра при известной пропускной способности V_c , м³/с и известных физических свойствах перемещаемой среды. Начинают расчет с назначения средней скорости движения среды с учетом условий движения и типа среды. Назначаемая скорость должна выбираться из рекомендуемых пределов, которые приводятся в таблицах приложений (например таблицы В.1 и В.2).

По известной пропускной способности и выбранной скорости движения потока из уравнения секундного расхода определяется площадь живого сечения потока. Учитывая форму живого сечения потока (круг, квадрат, прямоугольник и т.д.), находят определяющий геометрический размер потока. Так, для труб круглого сечения

Найденный определяющий геометрический размер потока необходимо согласовать с номенклатурой стандартных труб (таблицы В.4 – В.6) и выбрать ближайшую из труб, выпускаемых по ГОСТу. По принятому диаметру трубы d_ст рассчитывается средняя скорость движения среды. Полученные данные и будут являться исходными данными для дальнейших расчетов.

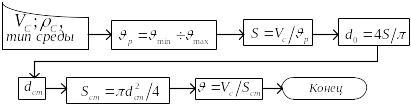
Блок – схема расчета диаметра трубы.

Понятие экономичной скорости

В простом трубопроводе ввиду постоянства его диаметра движение среды во всех его сечениях одинаково. Попробуем определить величину этой скорости, которая должна быть найвыгоднейшей с экономической точки зрения. Положим, что имеем водопроводную сеть, выполненную из труб определенного диаметра. Представим теперь, что диаметр труб данной сети начинаем уменьшать. В результате этого получаем следующее: скорость движения воды по сети возрастает ( ; потери напора в этих трубах будут также расти (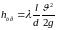 ), а следовательно, будет расти и потребляемая мощность насосов, перекачивающих воду ( ). Т.е. можно утверждать, что эксплуатационные затраты Э при этом возрастают. Также бесспорно выглядит и тот факт, что уменьшение диаметра труб магистрали снижает стоимость самой магистрали, т.е. величину капитальных затрат З_К на ее сооружение. Приводя капитальные затраты (с учетом срока окупаемости) и эксплуатационные затраты к единице перемещаемой среды, строят графики зависимости K_пр=f(d) и Э_пр=f(d) (см. рисунок 2.7). Тогда суммарные затраты З_пр выразятся кривой, полученной как сумма З_пр=Э_пр+К_пр=f(d). Абсцисса d_э определяет область экономически выгодного диаметра, а следовательно, и диаметра, при котором приведенные затраты будут минимальными, т.е. З_пр min.

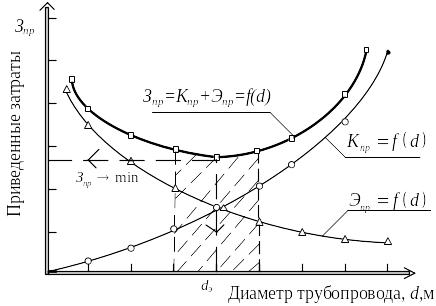
о – график зависимости приведенных капитальных затрат K_пр=f(d);

 – график зависимости приведенных эксплуатационных затрат Э_пр=f(d);

– результирующий график приведенных затрат З_пр=К_пр+Э_пр=f(d)

Рисунок 2.7 – К определению экономически выгодного диаметра

По В.С. Яблонскому, приближенно можно принять, что экономически наивыгоднейший диаметр обычно соответствует скорости примерно 1 м/с, т.е. диаметру, определяемому по формуле

где 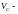секундный расход жидкости, м³/с. Для более точного определения наивыгоднейшего диаметра служат технико–экономические обоснования суть которых изложена выше.Проведенные рассуждения показали так же, что для определенного диаметра трубы есть своя экономичная скорость. Величина этой скорости для перемещения маловязких жидкостей в напорном трубопроводе лежит в пределах от 1 до 3 м/с. Ниже, в таблице 2.1, приведены экономичные скорости движения жидкости в трубах определенного диаметра, а в таблицах В.1 и В.2 приведены рекомендуемые скорости движения подвижных сред в трубах холодильных установок. Таблица 2.1 – Экономичные скорости движения жидкости в трубах различного диаметра

Размер условного прохода, Dy, м	0,10	0,20	0,25	0,30
Экономичная скорость, , м/с	0,75	0,90	1,10	1,25