12. Средняя, максимальная и местная скорость потока. Закон распределения скорости по сечению потока (закон Стокса). Соотношение между максимальной и средней скоростями потока при ламинарном режиме.

Средняя скорость потока - Скорость, с которой должны были бы двигаться все частицы жидкости через живое сечение потока, чтобы сохранился расход, соответствующий действительному распределению скоростей. Выражается формулой: V=Q/ω , где Q - расход потока, ω - площадь живого сечения потока.

Турбулентный поток характеризуется беспорядочным, хаотическим движением частиц жидкости. Наряду с основным поступательным пере-мещением жидкости вдоль трубы наблюдаются незакономерные попереч-ные перемещения и вращательные движения частиц, которые приводят к интенсивному перемешиванию жидкости. Вследствие интенсивного вих-реобразования частицы жидкости при турбулентном движении описывают весьма сложные траектории, а местные скорости не сохраняются постоян-ными даже в том случае, когда расход потока постоянен во времени. Таким образом, установившегося движения (в строгом понимании) в турбулент-ном потоке не существует. Измерения показывают, наоборот, что в каждой точке скорость непрерывно меняется как по величине, так и по направле-нию. Поэтому скорость в точке турбулентного потока называют мгновен-ной местной скоростью.

Выражение (5.4), характеризует закон распределения скоростей по живому сечению потока при ламинарном режиме движения жидкости и называется формулой Стокса.

Соотношение между средней скоростью и максимальной скоростью можно получить, сопоставив значение Q из уравнений

Таким образом, при ламинарном потоке в трубе средняя скорость жидкости равна половине скорости по оси трубы.

13. Расчет расхода жидкости при ламинарном режиме движения (уравнение Пуазейля).

Расход жидкости в круглой трубе при ее ламинарном движении определяется уравнением Пуазейля

, (4.10)

где d – внутренний диаметр трубы. гдеd,l– эквивалентный диаметр и длина канала, м;

μ – коэффициент динамической вязкости рабочей среды, Па·с; Δр=р₁ –р₂ – перепад давления на дросселе, Па.

14. Течение жидкости в малом зазоре . Уравнение Петрова. Создателем гидродинамической теории смазки является профессор Н. П. Петров. До него считали, что в подшипниках скольжения происходит трение одного тела (вала) о другое (вкладыш). Н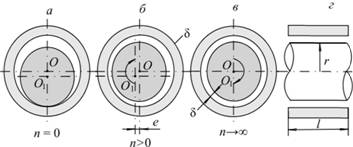 . П. Петров показал, что при вращении вал увлекает за собой смазочную жидкость, направляя ее в зазор между валом и вкладышем в нижней части (рис. 6.11, а). От этого давление в зазоре между валом и вкладышем возрастает. Образуется своего рода масляный клин, вытесняющий вал вверх и влево (рис. 6.11, б). При увеличении числа оборотов п вал "всплывает". Таким образом, трения вала о вкладыш не происходит – сухое трение заменяется жидкостным. При увеличении числа оборотов вал стремится встать в центре отверстия во вкладыше (центр вала О1 совпадает с центром подшипника О – рис. 6.11, в).

Вывод формулы Петрова для силы трения основывается на следующем. При одинаковой толщине слоя смазки

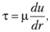где и – окружная скорость. При радиусе вата r и длине вкладыша l (рис. 6.11, г) полная поверхность, по которой происходит трение:

Тогда сила трения будет

Т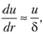 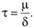ак как то

Отсюда

У читывая, что

г де – угловая скорость; п – число оборотов вала, получаем

Так как слой смазки неодинаков по толщине, то всегда имеет место эксцентриситет е, учитываемый поправочным коэффициентом  Окончательно формула Петрова принимает вид