1. Среднее значение (средняя арифметическая)
;
2. среднее линейное отклонение
;
3. дисперсия, рассчитанная по определению
;
4. дисперсия, рассчитанная по формуле разностей
,
где
;
5. среднее квадратическое отклонение
;
6. коэффициент вариации
;
7. асимметрия
;
8. эксцесс
.
Среднее значение, среднее линейное отклонение и среднее квадратическое отклонение являются именованными величинами. Дисперсия, асимметрия и эксцесс – неименованные величины. Если коэффициент вариации меньше 33%, то выборочная совокупность явялется плотной, однородной и по ней можно делать выводы, осуществлять прогнозы, выдвигать гипотезы.
Расчеты удобно производить в следующей таблице:
|
|
|
|
|
|
|
|
|
|
|
18,5 |
3 |
55,5 |
1026,75 |
-2,96 |
8,88 |
26,2848 |
-77,8030 |
230,2969 |
|
19,5 |
11 |
214,5 |
4182,75 |
-1,96 |
21,56 |
42,2576 |
-82,8249 |
162,3368 |
|
20,5 |
27 |
553,5 |
11346,75 |
-0,96 |
25,92 |
24,8832 |
-23,8879 |
22,9324 |
|
21,5 |
28 |
602,0 |
12943,00 |
0,04 |
1,12 |
0,0448 |
0,0018 |
0,0001 |
|
22,5 |
19 |
427,5 |
9618,75 |
1,04 |
19,76 |
20,5504 |
21,3274 |
22,2273 |
|
23,5 |
5 |
117,5 |
2761,75 |
2,04 |
10,20 |
20,808 |
42,4483 |
86,5946 |
|
24,5 |
3 |
73,5 |
1800,75 |
3,04 |
9,12 |
27,7248 |
84,2834 |
256,2215 |
|
25,5 |
4 |
102 |
2601,00 |
4,04 |
16,16 |
65,2864 |
263,7571 |
1065,5785 |
|
|
100 |
2146 |
46281 |
- |
112,72 |
227,84 |
227,3472 |
1846,1880 |
Получаем:
(мм);
(мм);
;
,
;
(мм);
;
;
.
Задача 5. Для выборки из задачи 1 методом моментов найти среднее значение дисперсию, асимметрию и эксцесс.
1. Находим шаг варьирования , то есть разность между любыми двумя соседними значениями случайной величины. Предполагается, что выборочной совокупности- постоянная величина.
2.
Величина ложного нуля
определяется как значение случайной
величины, имеющее максимальную частоту.
3. Для каждого значения х определяем условные варианты
.
4. Вычисляем условные моменты:
;
;
;
.
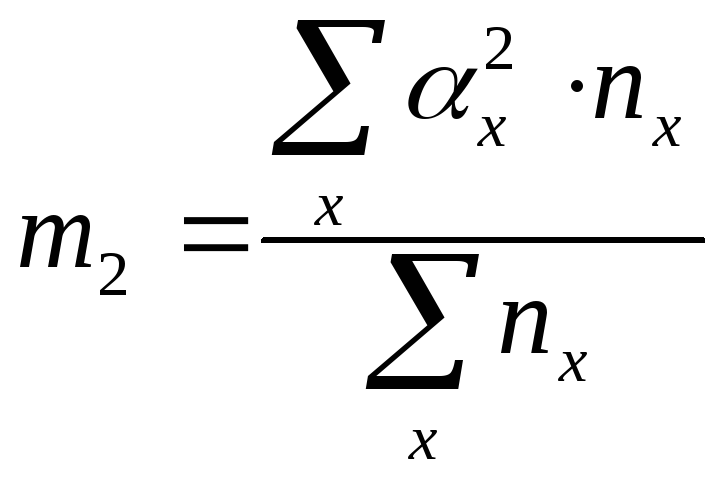5. Искомые значения рассчитываются по формулам:
;
;
;
.
Из группированного статистического ряда (см задачу 1) заключаем, что
=1.
Так как максимальной частоте ряда 28 соответствует значение случайной величины 21,5 (см. группированный статистический ряд, задача 1), то
=21,5.
Отсюда, условный вариант
.
Нахождение условных моментов удобно производить в таблице:
|
|
|
|
|
|
|
|
|
18,5 |
3 |
-3 |
-9 |
27 |
-81 |
243 |
|
19,5 |
11 |
-2 |
-22 |
44 |
-88 |
176 |
|
20,5 |
27 |
-1 |
-27 |
27 |
-27 |
27 |
|
21,5 |
28 |
0 |
0 |
0 |
0 |
0 |
|
22,5 |
19 |
1 |
19 |
19 |
19 |
19 |
|
23,5 |
5 |
2 |
10 |
20 |
40 |
80 |
|
24,5 |
3 |
3 |
9 |
27 |
81 |
243 |
|
25,5 |
4 |
4 |
16 |
64 |
256 |
1024 |
|
|
100 |
- |
-4 |
228 |
200 |
1812 |
Тогда, условные варианты соответственно равны:
;
;
;
.
Итак, требуемые величины соответственно равны:
;
;
;
.
Задача 6. Для выборки из задачи 1 с вероятностью γ = 0,95 определить границы интервала, в котором заключено математическое ожидание а (генеральная средняя или среднее значение генеральной совокупности) и сделать соответствующие выводы. Задачу решить в предположении а) повторного, б) бесповторного отбора из генеральной совокупности объема
N = 1500.
С доверительной вероятностью γ утверждается, что математическое ожидание а принадлежит интервалу:
,
где
- выборочная средняя (среднее значение
признака, рассчитанное по выборке),δ
– предельная
ошибка, равная
,
причем t – постоянная величина, значение которой определяется в зависимости от γ, в частности
t = 3, если γ=0,99,
t = 2, если γ=0,95,
t = 1, если γ=0,63,
μ – средняя ошибка выборки, равная