
МОС Задачник
.pdf
НАЦIОНАЛЬНИЙ УНIВЕРСИТЕТ "ОДЕСЬКА МОРСЬКА АКАДЕМIЯ"
МАТЕМАТИЧНI ОСНОВИ СУДНОВОДIННЯ
МЕТОДИЧНI ВКАЗIВКИ
ДО ВИКОНАННЯ ПРАКТИЧНИХ ЗАНЯТЬ
Одеса − 2019
НАЦIОНАЛЬНИЙ УНIВЕРСИТЕТ "ОДЕСЬКА МОРСЬКА АКАДЕМIЯ"
КАФЕДРА СУДНОВОДIННЯ
МАТЕМАТИЧНI ОСНОВИ СУДНОВОДIННЯ
МЕТОДИЧНI ВКАЗIВКИ
ДО ВИКОНАННЯ ПРАКТИЧНИХ ЗАНЯТЬ
для курсантiв 2 курсу ФМП і Т (зі скороченим терміном навчання)
Виконавець(і):
Астайкін Д.В., доцент; Сікірін В.Є., доцент; Фусар I.Ю., старший викладач.
Затверджено на засіданні кафедри судноводіння, як методичнi вказiвки до виконання практичних занять з дисципліни "МОС" для курсантів 2 курсу ФМП і Т (зі скороченим терміном навчання)
Протокол № 2 від 10.09.2019.
зав.каф. проф. Алексішин В.Г._____________
Одесса − 2019
СОДЕРЖАНИЕ
№ |
Название тем |
Стр. |
||
|
|
|
|
|
1. |
Практическая работа № 1. Приближенные вычисления. Правила подсчета |
2 |
– 5 |
|
цифр. Приближенные вычисления. Метод границ. |
||||
|
|
|
||
|
|
|
|
|
2. |
Практическая работа № 2. Абсолютная и относительная погрешности в |
6 |
– 9 |
|
задачах судовождения. Интерполяция (таблицы). |
||||
|
|
|
||
|
|
|
|
|
|
Практическая работа № 3. Сферические треугольники в задачах |
|
|
|
3. |
судовождения. Решение прямоугольных и четвертных сферических |
10 |
– 13 |
|
|
треугольников. |
|
|
|
|
|
|
|
|
4. |
Практическая работа № 4. Выбор оптимального маршрута судна. |
14 |
– 16 |
|
|
|
|||
|
|
|
|
|
5. |
Практическая работа № 5. Обработка равноточных и неравноточных |
|
|
|
наблюдений. |
17 |
– 22 |
||
|
||||
|
|
|
||
|
|
|
|
|
6. |
Практическая работа № 6. Расчет элементов линии положения. ОМС |
|
|
|
графически и аналитически. |
23 |
– 27 |
||
|
||||
|
|
|
||
|
|
|
|
|
7. |
Практическая работа № 7. Оценка точности обсервации эллипсом |
|
|
|
погрешностей. Эллипс погрешностей при равноточных ЛП. |
28 |
– 32 |
||
|
||||
|
|
|
||
|
|
|
|
|
8. |
Практическая работа № 8. Оценка точности обсервации круговой |
|
|
|
погрешностью |
33 |
– 34 |
||
|
||||
|
|
|
||
|
|
|
|
|
|
Приложение 1. |
|
35 |
|
|
|
|
|
|
|
Приложение 2. |
|
35 |
|
|
|
|
|
|
|
Приложение 3. |
|
36 |
|
|
|
|
|
|
|
Список литературы. |
|
37 |
|
|
|
|
|
|

ПРАКТИЧЕСКАЯ РАБОТА № 1.
1. Приближенные вычисления. Правила подсчета цифр.
Различают приближенные вычисления со строгим учетом погрешностей и без строгого учета. В менее ответственных вычислениях с приближенными числами пользуются вторым способом, основанным на так называемых правилах подсчета цифр. В этих правилах используются понятия десятичных знаков, значащих, точных и сомнительных цифр. Напомним, что десятичными знаками числа называют все его цифры, стоящие правее запятой . Например, числа 3,5 и 3,05 имеют соответственно один и два десятичных знака.
Правила подсчета цифр.
1. При сложении и вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их в приближенном данном с наименьшим числом десятичных знаков.
Пример. Найти сумму приближенных чисел 127,42; 67,3; 0,12 и 3,03.
127,42
67,3
0,12
3,03
197,87 ≈ 197,9.
2. При умножении и делении приближенных чисел в результате надо сохранить столько значащих цифр, сколько их есть в данном числе с наименьшим количеством значащих цифр.
Пример. Умножить приближенные числа 3,4 и 12,32.
12,32 ∙ 3,4 = 41,888 ≈ 42.
3. При возведении приближенных чисел в квадрат и куб в результате сохраняется столько значащих цифр, сколько их в основании.
Пример. Возвести в квадрат число 2,3, возвести в третью степень число 0,8.
2,32 = 5,29 ≈ 5,3;
0,83 = 0,512 ≈ 0,5.
4.В промежуточных результатах следует брать одной цифрой больше, чем рекомендуют предыдущие правила.
5.Если некоторые данные имеют больше десятичных знаков (при действиях первой ступени) или больше значащих цифр (при действиях II и III ступеней), чем другие, то их предварительно следует округлить, сохраняя лишь одну запасную цифру.
6.Если данные можно брать с произвольной точностью, то для получения результата с k цифрами данные следует брать с таким числом цифр, которое дает согласно перечисленным правилам k + 1 цифру в результате.
Применение вычислений способом подсчета цифр рассмотрим на примере.
Пример. Найти значение |
, если a ≈ 9.31, b ≈ 3.1, c ≈ 2.33. |
|
a – b = 9.31 – 3.1 = 6.21, |
|
(a – b)c = 6.21 ∙ 2.33 ≈ 14.5, |
|
a + b = 9.31 + 3.1 ≈ 12.4, |
Ответ: |
x = 14.5 / 12.4 ≈ 1.2. |
2
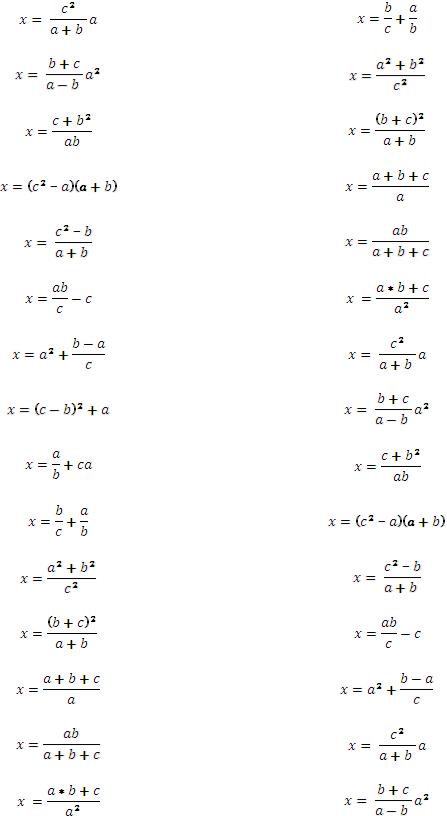
Задания для индивидуальной работы.
По данным таблицы 1 найти значение выражения используя правила подсчета цифр.
Таблица 1 - Варианты для выполнения индивидуальных заданий
№ |
Выражение |
Значения |
№ |
Выражение |
Значения |
|||
переменных |
переменных |
|||||||
|
|
|
|
|||||
|
|
a ≈ 3,59; |
|
|
a ≈ 5,75; |
|||
1.1 |
|
b |
≈ 3,661; |
1.16 |
|
b |
≈ 4,318; |
|
|
|
|
c ≈ 3,6. |
|
|
|
c ≈ 9,4. |
|
|
|
a ≈ 9,72; |
|
|
a ≈ 9,66; |
|||
1.2 |
|
b |
≈ 9,297; |
1.17 |
|
b |
≈ 5,492; |
|
|
|
|
c ≈ 7,1. |
|
|
|
c ≈ 1,2. |
|
|
|
a ≈ 3,01; |
|
|
a ≈ 6,02; |
|||
1.3 |
|
b |
≈ 4,735; |
1.18 |
|
b |
≈ 5,147; |
|
|
|
|
c ≈ 3,7. |
|
|
|
c ≈ 2,4. |
|
|
|
a ≈ 5,12; |
|
|
a ≈ 9,35; |
|||
1.4 |
|
b |
≈ 2,297; |
1.19 |
|
b |
≈ 8,307; |
|
|
|
|
c ≈ 7,3. |
|
|
|
c ≈ 2,2. |
|
|
|
a ≈ 1,73; |
|
|
a ≈ 9,21; |
|||
1.5 |
|
b |
≈ 2,029; |
1.20 |
|
b |
≈ 9,223; |
|
|
|
|
c ≈ 9,8. |
|
|
|
c ≈ 2,7. |
|
|
|
a ≈ 1,29; |
|
|
a ≈ 2,18; |
|||
1.6 |
|
b |
≈ 9,451; |
1.21 |
|
b |
≈ 3,564; |
|
|
|
|
c ≈ 5,4. |
|
|
|
c ≈ 2,5. |
|
|
|
a ≈ 5,02; |
|
|
a ≈ 2,44; |
|||
1.7 |
|
b |
≈ 9,273; |
1.22 |
|
b |
≈ 9,498; |
|
|
|
|
c ≈ 4,8. |
|
|
|
c ≈ 1,4. |
|
|
|
a ≈ 3,05; |
|
|
a ≈ 5,54; |
|||
1.8 |
|
b |
≈ 2,918; |
1.23 |
|
b |
≈ 2,808; |
|
|
|
|
c ≈ 9,6. |
|
|
|
c ≈ 8,4. |
|
|
|
a ≈ 7,93; |
|
|
a ≈ 6,95; |
|||
1.9 |
|
b |
≈ 1,616; |
1.24 |
|
b |
≈ 5,086; |
|
|
|
|
c ≈ 9,6. |
|
|
|
c ≈ 3,2. |
|
|
|
a ≈ 3,38; |
|
|
a ≈ 7,42; |
|||
1.10 |
|
b ≈ 5,404; |
1.25 |
|
b ≈ 6,177; |
|||
|
|
|
c ≈ 8,1. |
|
|
|
c ≈ 9,3. |
|
|
|
a ≈ 7,15; |
|
|
a ≈ 8,15; |
|||
1.11 |
|
b |
≈ 8,591; |
1.26 |
|
b |
≈ 1,552; |
|
|
|
|
c ≈ 3,7. |
|
|
|
c ≈ 5,3. |
|
|
|
a ≈ 5,73; |
|
|
a ≈ 1,93; |
|||
1.12 |
|
b |
≈ 9,818; |
1.27 |
|
b |
≈ 2,725; |
|
|
|
|
c ≈ 5,5. |
|
|
|
c ≈ 5,2. |
|
|
|
a ≈ 3,41; |
|
|
a ≈ 1,77; |
|||
1.13 |
|
b |
≈ 1,646; |
1.28 |
|
b |
≈ 2,931; |
|
|
|
|
c ≈ 6,6. |
|
|
|
c ≈ 3,9. |
|
|
|
a ≈ 3,79; |
|
|
a ≈ 3,25; |
|||
1.14 |
|
b |
≈ 3,326; |
1.29 |
|
b |
≈ 5,356; |
|
|
|
|
c ≈ 3,9. |
|
|
|
c ≈ 9,5. |
|
|
|
a ≈ 7,33; |
|
|
a ≈ 6,66; |
|||
1.15 |
|
b |
≈ 7,407; |
1.30 |
|
b |
≈ 8,635; |
|
|
|
|
c ≈ 4,5. |
|
|
|
c ≈ 5,6. |
|
3
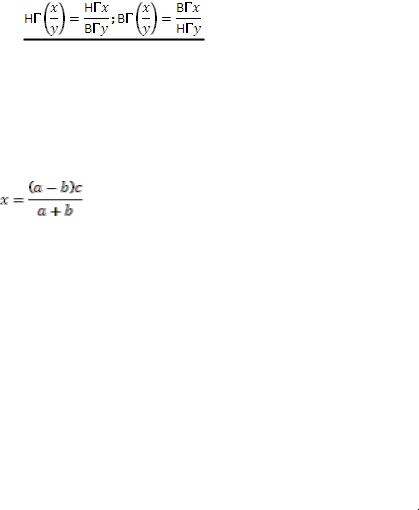
2. Приближенные вычисления. Метод границ.
Вычисления способом подсчета цифр − самый грубый способ оценки погрешности результата действий.
В более ответственных вычислениях пользуются способом границ или способом граничных погрешностей.
Приближенные вычисления по способу границ.
Наилучшим в смысле строгости из известных способов приближенных вычислений является способ границ. Пользуясь этим способом, по известным нижним и верхним границам данных чисел находят отдельно нижнюю и верхнюю границы результата.
Нижняя граница суммы приближенных чисел равна сумме нижних границ слагаемых, а верхняя − сумме верхних границ слагаемых. Символически это можно записать так:
НГ(х + у) = НГx + НГу; ВГ(х + у) = ВГx + ВГу.
Аналогичные правила справедливы для умножения:
НГ(xу) = НГx • НГу; ВГ(ху) = ВГx • ВГy.
Для обратных действий − вычитания и деления − соответствующие правила имеют
вид:
НГ(х — у) = НГх — ВГу; ВГ(х — у) = ВГх — НГу.
Из определения НГ и ВГ вытекают также следующие правила:
−округлять НГ можно только по недостатку, а ВГ − по избытку;
−чем меньше разность ВГх – НГх, тем точнее определяется х;
−в качестве приближенного значения х рекомендуется брать среднее арифметическое чисел НГх и ВГх или число близкое к нему.
Пример. Дано выражение: |
|
|
|
|
Определить: найти значение x, если a ≈ 9,21(±0,01); |
b ≈ 3,05(±0,02); c ≈ 2,33(±0,01). |
|||
Решение: Определяем НГ и ВГ каждого из этих чисел, выполнив над ними |
||||
соответствующие действия, находим НГ и ВГ числа х. |
|
|
||
Запись удобно оформить в виде таблицы. |
|
|
||
Таблица записи НГ и ВГ каждого из чисел |
|
|
||
|
|
|
|
|
Компоненты |
|
НГ |
|
ВГ |
|
|
|
|
|
a |
|
9,20 |
|
9,22 |
b |
|
3,03 |
|
3,07 |
c |
|
2,32 |
|
2,34 |
a – b |
|
6,13 |
|
6,19 |
(a-b) ∙ c |
|
14,22 |
|
14,49 |
a + b |
|
12,23 |
|
12,29 |
x |
|
1,15 |
|
1,19 |
1 , 1 5 < x < 1 , 1 9 . 2 , 3 4 / 2 = 1 , 1 7 . 0 , 0 4 / 2 = 0 , 0 2 .
Ответ: x ≈ 1,17 (± 0,02).
4

Задания для индивидуальной работы.
По данным таблицы 2 найти значение выражения используя правила подсчета цифр.
Таблица 2 − Варианты для выполнения индивидуальных заданий
№ |
Выражение |
Значения |
№ |
Выражение |
|
Значения |
переменных |
|
переменных |
||||
|
|
|
|
|
||
|
|
a ≈ 3,59(±0,01); |
|
|
a ≈ 5,75(±0,01); |
|
2.1 |
|
b ≈ 3,66(±0,02); |
2.16 |
|
b |
≈ 4,31(±0,01); |
|
|
c ≈ 3,63(±0,01). |
|
|
c ≈ 9,45(±0,03). |
|
|
|
a ≈ 9,72 (±0,02); |
|
|
a ≈ 9,66(±0,02); |
|
2.2 |
|
b ≈ 9,29(±0,01); |
2.17 |
|
b |
≈ 5,49(±0,02); |
|
|
c ≈ 7,14(±0,01). |
|
|
c ≈ 1,28(±0,01). |
|
|
|
a ≈ 3,01(±0,01); |
|
|
a ≈ 6,02(±0,01); |
|
2.3 |
|
b ≈ 4,73(±0,01); |
2.18 |
|
b |
≈ 5,14(±0,01); |
|
|
c ≈ 3,74(±0,02). |
|
|
c ≈ 2,47(±0,02). |
|
|
|
a ≈ 5,12(±0,02); |
|
|
a ≈ 9,35(±0,01); |
|
2.4 |
|
b ≈ 2,29(±0,02); |
2.19 |
|
b |
≈ 8,30(±0,03); |
|
|
c ≈ 7,31((±0,01). |
|
|
c ≈ 2,25(±0,01). |
|
|
|
a ≈ 1,73(±0,01); |
|
|
a ≈ 9,21(±0,01); |
|
2.5 |
|
b ≈ 2,02(±0,02); |
2.20 |
|
b |
≈ 9,22(±0,02); |
|
|
c ≈ 9,86(±0,02). |
|
|
c ≈ 2,75(±0,03). |
|
|
|
a ≈ 1,29(±0,01); |
|
|
a ≈ 2,18(±0,01); |
|
2.6 |
|
b ≈ 9,45(±0,01); |
2.21 |
|
b |
≈ 3,56 (±0,01); |
|
|
c ≈ 5,48(±0,02). |
|
|
c ≈ 2,45(±0,02). |
|
|
|
a ≈ 5,02(±0,02); |
|
|
a ≈ 2,44(±0,01); |
|
2.7 |
|
b ≈ 9,27(±0,01); |
2.22 |
|
b |
≈ 9,49(±0,03); |
|
|
c ≈ 4,86(±0,01). |
|
|
c ≈ 1,44(±0,01). |
|
|
|
a ≈ 3,05((±0,01); |
|
|
a ≈ 5,54(±0,02); |
|
2.8 |
|
b ≈ 2,91(±0,02); |
2.23 |
|
b |
≈ 2,80(±0,01); |
|
|
c ≈ 9,63(±0,02). |
|
|
c ≈ 8,45(±0,02). |
|
|
|
a ≈ 7,93(±0,01); |
|
|
a ≈ 6,95(±0,02); |
|
2.9 |
|
b ≈ 1,61(±0,01); |
2.24 |
|
b |
≈ 5,08(±0,01); |
|
|
c ≈ 9,68(±0,02). |
|
|
c ≈ 3,24(±0,01). |
|
|
|
a ≈ 3,38(±0,03); |
|
|
a ≈ 7,42(±0,01); |
|
2.10 |
|
b ≈ 5,40(±0,01); |
2.25 |
|
b |
≈ 6,17(±0,02); |
|
|
c ≈ 8,14(±0,01). |
|
|
c ≈ 9,34(±0,02). |
|
|
|
a ≈ 7,15(±0,01); |
|
|
a ≈ 8,15(±0,02); |
|
2.11 |
|
b ≈ 8,59(±0,02); |
2.26 |
|
b |
≈ 1,55(±0,01); |
|
|
c ≈ 3,71(±0,01). |
|
|
c ≈ 5,3(±0,02). |
|
|
|
a ≈ 5,73(±0,01); |
|
|
a ≈ 1,93(±0,01); |
|
2.12 |
|
b ≈ 9,81(±0,02); |
2.27 |
|
b |
≈ 2,72(±0,01); |
|
|
c ≈ 5,85(±0,01). |
|
|
c ≈ 5,24(±0,03) |
|
|
|
a ≈ 3,41(±0,01); |
|
|
a ≈ 1,77(±0,01); |
|
2.13 |
|
b ≈ 1,64(±0,03); |
2.28 |
|
b |
≈ 2,93(±0,01); |
|
|
c ≈ 6,62(±0,02). |
|
|
c ≈ 3,9(±0,02). |
|
|
|
a ≈ 3,79(±0,01); |
|
|
a ≈ 3,25(±0,01); |
|
2.14 |
|
b ≈ 3,32(±0,02); |
2.29 |
|
b |
≈ 5,35(±0,01); |
|
|
c ≈ 3,93(±0,03). |
|
|
c ≈ 9,55(±0,03). |
|
|
|
a ≈ 7,33(±0,02); |
|
|
a ≈ 6,66(±0,01); |
|
2.15 |
|
b ≈ 7,40(±0,01); |
2.30 |
|
b |
≈ 8,63(±0,02); |
|
|
c ≈ 4,54(±0,02). |
|
|
c ≈ 5,63(±0,01). |
|
5
ПРАКТИЧЕСКАЯ РАБОТА № 2.
1. Абсолютная и относительная погрешности в задачах судовождения.
Абсолютная погрешность (Absolute error ) " " – разность между истинной величиной и ее приближенным значением. = А – а, где А -истинное число.
Например, если точное число 1,214 округлить до десятых, получим приближенное число 1,2. В данном случае абсолютная погрешность приближенного числа 1,2 равна
1,214 – 1,2: т. е. 0,014.
Но в большинстве случаев известно только приближенное значение рассматриваемой величины. Тогда абсолютная погрешность неизвестна.
В этих случаях указывают границу, которую она не превышает. Это число называют
граничной абсолютной погрешностью.
Граничную абсолютную погрешность приближенного числа а обозначают символом .
А ≈ а (±Δ).
Запись следует понимать так: точное значение величины А находится в промежутке между числами а - и а + Δ, которые называют соответственно нижней и верхней границами А и обозначают НГА и ВГА.
Пример: если А ≈ 2,3(± 0,1), то 2,2 < А < 2,4. Наоборот, если 7,3 < А < 7,4, то А ≈ 7,35(± 0,05).
Относительная погрешность (Relative error), "δ" – отношение абсолютной погрешности к величине приближенного числа.
Отношение граничной абсолютной погрешности к приближенному числу называют граничной относительной погрешностью: δ = / а.
Относительную и граничную относительную погрешности принято выражать в
процентах. |
|
Пример. |
12,3 < А <12,7. |
Ответ: |
а = 12,5 (± 0,2). = 0,2. |
|
δ = 0,2 / 12,5 = 0,016 = 1,6%. |
Пример. Накопительный зерновой терминал порта принимает груз через два весовых комплекса. Точность взвешивания одной тонны груза на первом комплексе - ± 0,015т. , на втором – ± 0,013т.
Определить относительную погрешность веса принятого груза, если через первый
комплекс прошло 10000т. зерна, |
через второй – 5000т. |
Решение: Определим абсолютную погрешность измерений каждого комплекса: |
|
Первый комплекс - 10 000 (± 150)т. |
|
Второй комплекс - |
5 000 (± 65) т. |
Определяем суммарную абсолютную погрешность обеих комплексов:
10 000 (± 150) + 5 000 (± 65) = 15 000 (± 215)т.
Находим относительную погрешность принятого груза:
Ответ: δ = 215 / 15000 = 0,01433 = 1,4%.
6
Задания для индивидуальной работы.
Накопительный зерновой терминал порта принимает груз через два весовых комплекса – А и Б. По данным табл. 3 определить относительную погрешность (δ) принятого груза.
Таблица 3 – Варианты для выполнения индивидуальных заданий
|
Комплекс А |
Комплекс Б |
|||
|
|
|
|
|
|
Вариант |
|
Точность |
|
Точность |
|
Количество зерна |
взвешивания |
Количество зерна |
взвешивания |
||
№ |
|||||
(т) |
1 тонны груза |
(т) |
1 тонны груза |
||
|
|||||
|
|
(±…т) |
|
(±…т) |
|
|
|
|
|
|
|
3.1 |
11652 |
0,013 |
17787 |
0,014 |
|
|
|
|
|
|
|
3.2 |
7044 |
0,012 |
15133 |
0,013 |
|
|
|
|
|
|
|
3.3 |
7404 |
0,015 |
7344 |
0,015 |
|
|
|
|
|
|
|
3.4 |
14064 |
0,013 |
8052 |
0,014 |
|
|
|
|
|
|
|
3.5 |
5784 |
0,01 |
11012 |
0,009 |
|
|
|
|
|
|
|
3.6 |
16856 |
0,01 |
18218 |
0,015 |
|
|
|
|
|
|
|
3.7 |
7044 |
0,015 |
18458 |
0,01 |
|
|
|
|
|
|
|
3.8 |
7155 |
0,012 |
18299 |
0,015 |
|
|
|
|
|
|
|
3.9 |
11261 |
0,014 |
9375 |
0,016 |
|
|
|
|
|
|
|
3.10 |
18504 |
0,01 |
18790 |
0,011 |
|
|
|
|
|
|
|
3.11 |
16433 |
0,011 |
9261 |
0,015 |
|
|
|
|
|
|
|
3.12 |
17396 |
0,015 |
7531 |
0,015 |
|
|
|
|
|
|
|
3.13 |
18187 |
0,014 |
9379 |
0,009 |
|
|
|
|
|
|
|
3.14 |
18423 |
0,014 |
9444 |
0,014 |
|
|
|
|
|
|
|
3.15 |
12445 |
0,014 |
9418 |
0,016 |
|
|
|
|
|
|
|
3.16 |
17879 |
0,012 |
10824 |
0,015 |
|
|
|
|
|
|
|
3.17 |
8972 |
0,013 |
14141 |
0,013 |
|
|
|
|
|
|
|
3.18 |
15907 |
0,015 |
5968 |
0,014 |
|
|
|
|
|
|
|
3.19 |
14325 |
0,01 |
9110 |
0,009 |
|
|
|
|
|
|
|
3.20 |
14283 |
0,016 |
5673 |
0,009 |
|
|
|
|
|
|
|
3.21 |
19515 |
0,016 |
16574 |
0,01 |
|
|
|
|
|
|
|
3.22 |
8119 |
0,009 |
6105 |
0,014 |
|
|
|
|
|
|
|
3.23 |
10753 |
0,011 |
15954 |
0,014 |
|
|
|
|
|
|
|
3.24 |
12383 |
0,011 |
9670 |
0,011 |
|
|
|
|
|
|
|
3.25 |
14111 |
0,011 |
15168 |
0,013 |
|
|
|
|
|
|
|
3.26 |
8620 |
0,015 |
9667 |
0,013 |
|
|
|
|
|
|
|
3.27 |
15893 |
0,011 |
19469 |
0,016 |
|
|
|
|
|
|
|
3.28 |
16987 |
0,014 |
12858 |
0,014 |
|
|
|
|
|
|
|
3.29 |
7500 |
0,014 |
18067 |
0,014 |
|
|
|
|
|
|
|
3.30 |
16054 |
0,012 |
17184 |
0,015 |
|
|
|
|
|
|
|
7
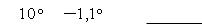
2. Интерполяция (таблицы).
В процессе своей работы судоводитель сталкивается с множеством задач, решение которых производится с помощью специальных таблиц. В зависимости от числа аргументов они бывают одно–, двух–, иногда трех–аргументными таблицами.
По способу нахождения необходимого значения таблицы бывают безинтерполяционные и интерполяционные. Самыми простыми являются безинтерполяционные таблицы. В них для определенного интервала аргумента приводится одно значение функции. В интерполяционных таблицах значение функции дано для некоторых фиксированных значений аргумента.
Рассмотрим пример работы с одноаргументной таблицей девиации магнитного компаса.
Пример. С помощью таблицы девиации магнитного компаса определить девиацию магнитного компаса (δ), если известно, что КК = 23,6º.
Решение: Выбираем девиацию для ближайших значений КК (20º и 30º).
КК |
δ |
|
|
20º |
+3,1º |
|
|
30º |
+2,0º |
|
|
За начальную девиацию примем значение соответствующее КК=20º. Чтобы определить девиацию для КК=23,6º необходимо провести интерполяцию.
Для этого составим пропорцию.
При изменении КК на 10º δ изменяется на – 1,1º.
Необходимо найти на сколько измениться δ при изменении курса на 3,6º.
х 3,6 ( 1,1) 0,40 10
Рассчитав изменение δ можно определить и само ее значение:
δ = +3,1 + (– 0,4) = +2,7º.
Ответ: δ =+2,7º.
В качестве примера многоаргументной таблицы рассмотрим "Таблицу поправок к моментам восхода и захода Солнца и Луны, сумерек и кульминаций светил" из пособия
МАЕ.
Пример. Дано: табличный интервал широт 5º, Δφ=3º 41’, табличная разность моментов (ΔТ) – 1ч22м.
Определить: с помощью таблицы (Приложение 1) определить поправку за широту к времени восхода Солнца.
Решение: Выбираем поправку для ближайших значений разности широт и разностей моментов:
Табличный |
5º |
Разность шрот Δφ |
||
интервал широт |
|
|
||
3º 30’ |
4º 00’ |
|||
|
||||
|
|
|
|
|
Табличные разности |
1ч20м |
41м |
52м |
|
моментов |
|
|
|
|
1ч24м |
42м |
54м |
||
|
|
|
|
|
8
