
МОС Задачник
.pdfДля нахождения поправки необходимо провести двойную интерполяцию по разности моментов по разности широт. Проведем сперва интерполяцию по Т.
При изменении Т на +4 минуты (1ч24м – 1ч20м) поправки меняются на +1м (для
Δφ=3º30’) и на +2м (для Δφ=4º00’). |
|
|
|
|
|
|
|
|
Найдем значение поправок при изменении |
Т на +2 минуты (1ч22м – 1ч20м). Составим |
|||||||
пропорции: |
|
|
|
|
|
|
|
|
|
4 м |
+1 |
4 м |
+2 |
|
|||
|
2 м |
x |
2 м |
x |
|
|||
х |
2 ( 1) |
0,5м |
х |
2 ( 2) |
|
1м |
||
|
4 |
|
|
|
|
4 |
|
|
Таким образом для Δφ=3º30' поправка будет равна |
41,5 минуты (41+0,5), а для |
|||||||
Δφ=4º00'– 53 минуты (52м +1 м).
Проведем интерполяцию по Δφ. При изменении Δφ на +30' поправка меняется на +11,5 минут. Найдем изменение поправки при изменении Δφ на +11' с помощью пропорции:
30' |
+11,5 |
|||
11' |
x |
|
||
х |
11 ( 11,5) |
|
4м |
|
|
||||
|
|
30 |
|
|
Рассчитав изменение поправки, найдем и само значение: 41,5 + 4 = 45,5 минут.
Ответ: +45,5 минут.
Задания для индивидуальной работы.
По данным таблицы 4, с помощью (Приложение 1) определить поправку за широту к времени восхода Солнца.
Таблица 4 – Варианты для выполнения индивидуальных заданий
№ |
Δφ |
Т |
Табличный интервал широт |
№ |
Δφ |
Т |
Табличный интервал широт |
№ |
Δφ |
Т |
Табличный интервал широт |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4.1 |
1º20' |
1ч38м |
2º |
4.11 |
4º38' |
1ч10м |
5º |
4.21 |
6º29' |
1ч27м |
10º |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.2 |
4 |
38 |
1 |
02 |
5 |
4.12 |
5 |
45 |
1 |
39 |
10 |
4.22 |
1 |
40 |
1 |
25 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3 |
8 |
22 |
1 |
17 |
10 |
4.13 |
1 |
30 |
1 |
27 |
2 |
4.23 |
4 |
55 |
1 |
18 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4 |
1 |
53 |
1 |
38 |
2 |
4.14 |
4 |
20 |
0 |
55 |
5 |
4.24 |
7 |
32 |
1 |
14 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.5 |
4 |
17 |
0 |
37 |
5 |
4.15 |
8 |
27 |
1 |
36 |
10 |
4.25 |
1 |
30 |
1 |
39 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.6 |
8 |
40 |
0 |
45 |
10 |
4.16 |
1 |
21 |
1 |
05 |
2 |
4.26 |
2 |
42 |
1 |
33 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.7 |
1 |
52 |
0 |
42 |
2 |
4.17 |
3 |
10 |
1 |
34 |
5 |
4.27 |
6 |
15 |
1 |
30 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.8 |
3 |
47 |
0 |
59 |
5 |
4.18 |
7 |
41 |
1 |
31 |
10 |
4.28 |
1 |
19 |
0 |
57 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.9 |
7 |
35 |
1 |
25 |
10 |
4.19 |
1 |
54 |
0 |
53 |
2 |
4.29 |
4 |
55 |
0 |
46 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.10 |
1 |
53 |
1 |
26 |
2 |
4.20 |
3 |
50 |
1 |
11 |
5 |
4.30 |
9 |
25 |
1 |
35 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9
ПРАКТИЧЕСКАЯ РАБОТА № 3.
1. Сферические треугольники в задачах судовождения.
Сферический треугольник – часть сферы, которая образуется при попарном пересечении трех дуг больших кругов. В сферических треугольниках и стороны и углы измеряются в градусной мере.
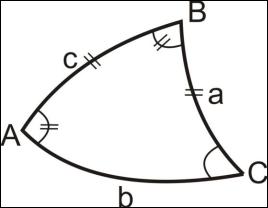
Вершины сферического треугольника обозначаются заглавными буквами A, B, C, а противолежащие им стороны одноименными малыми буквами a, b, c. (Рис.1.1). Стороны и углы при вершинах называются элементами сферического треугольника.
Рис. 1.1 – Сферический треугольник
Будем рассматривать треугольники Эйлера – сферические треугольники, элементы которых меньше 180˚.
При решении сферических треугольников необходимо знать как минимум три из шести его элементов. В сферическом треугольнике (Рис. 1.1), лежащие рядом элементы обозначим двумя черточками. В нашем случае угол "А" и сторона "a" будут крайними элементами, а сторона "c" и угол "B" – средними элементами. Для нахождения неизвестных элементов будем использовать четыре основные теоремы сферической тригонометрии:
Теорема косинуса стороны.
Во всяком сферическом треугольнике косинус стороны равен сумме произведения косинусов двух других сторон и произведения синусов этих сторон на косинус угла между ними: cos a cosb cos c sin b sin c cos A .
Теорема косинуса угла.
Во всяком сферическом треугольнике косинус угла равен сумме отрицательного произведения косинусов двух других углов и произведения синусов этих углов на косинус стороны между ними:
Теорема котангенсов (четырех рядом лежащих элементов).
В сферическом треугольнике для четырех рядом лежащих элементов котангенс крайнего угла, умноженный на синус среднего угла равен произведению котангенса крайней стороны на синус средней стороны, минус произведение косинусов средних
элементов: ctgA sin B ctga sin c cos B cos c |
(3.1) |
10

Формулу (8.1) можно упростить, воспользовавшись тригонометрическим тождеством:
ctg = 1 / tg. |
|
После преобразований получим: tg A = sin B / (sin c / tg a – cos B ∙ cos c) |
(3.2) |
Если в результате элемент А, найденный по формуле (3.1) получится отрицательным,
то к нему необходимо прибавить 180˚.
Теорема синусов.
Во всяком сферическом треугольнике отношения синусов углов к синусам противолежащих сторон равны: sin A / sin a sin B / sin b sin C / sin c (2.5)
Для определения неизвестных элементов будем пользоваться первыми тремя теоремами. Теорему синусов необходимо использовать только для проверки.
Пример. В сферическом треугольнике заданы две стороны и угол между ними: b = 37˚27,9′; A = 109˚48,6′; c = 140˚40,4′.
Определить: a, B, C.
Решение.
Если микрокалькулятор не дает возможность записывать числа в градусах и минутах, необходимо перевести значения заданных элементов в градусы. Для этого значения минут делим на 60 и прибавляем к значениям градусов.
b = 37˚27,9′ = 37,465˚; A = 109˚48,6′ = 109,810˚; c = 140˚40,4′=140,673˚.
Запишем основные теоремы для нашего примера:
cos a = cos b cos c + sin b sin c cos A;
ctg B sin A = ctg b sin c – cos A cos c;
ctg C sin A = ctg c sin b – cos b cos A.
Выразим неизвестные элементы и получим рабочие формулы: cos a = cos b cos c + sin b sin c cos A; tg B = sin A / (sin c / tg b – cos A cos c); tg C = sin A / (sin b / tg c – cos b cos A);
После подстановки заданных элементов получим:
cos a = – 0,7446 a = arcos (-0,7446) = 138 07,6′. tg B = 1,6657 B = arctg (1,6657) = 59 01,4′.
tg C = – 1,9871 C = arctg (-1,9871) = 116 42,8′.
Проверка: sin A / sin a = 1,409508; sin B / sin b = 1,409508; sin C / sin c = 1,409508. Ответ: a =138 07,6′; B = 59 01,4′; C = 116 42,8′
11
Задания для индивидуальной работы.
В задачах № 5.1 ÷ 5.30 заданы две стороны и угол сферического треугольника : a, b, C.
По данным таблицы 5, определить два угла и сторону: A, B, c.
Таблица 5 – Варианты для выполнения индивидуальных заданий
№ |
a |
b |
C |
№ |
a |
b |
C |
|
|
|
|
|
|
|
|
5.1 |
90º21,7' |
135º33,5' |
129º15,0' |
5.16 |
154º26,9' |
126º47,9' |
96º54,3' |
|
|
|
|
|
|
|
|
5.2 |
37 27,9 |
140 40,4 |
109 48,6 |
5.17 |
5 58,7 |
87 20,3 |
52 03,4 |
|
|
|
|
|
|
|
|
5.3 |
81 27,5 |
115 56,5 |
25 43,2 |
5.18 |
60 23,0 |
107 53,0 |
72 48,3 |
|
|
|
|
|
|
|
|
5.4 |
107 00,6 |
123 37,3 |
54 37,4 |
5.19 |
129 44,5 |
100 57,2 |
112 22,8 |
|
|
|
|
|
|
|
|
5.5 |
96 51,4 |
135 35,4 |
90 07,7 |
5.20 |
46 58,3 |
49 34,4 |
96 57,2 |
|
|
|
|
|
|
|
|
5.6 |
70 35,1 |
143 31,2 |
25 21,4 |
5.21 |
112 44,9 |
95 18,0 |
71 29,9 |
|
|
|
|
|
|
|
|
5.7 |
32 42,7 |
38 34,0 |
145 56,4 |
5.22 |
136 48,2 |
110 40,1 |
113 53,1 |
|
|
|
|
|
|
|
|
5.8 |
128 21,6 |
132 26,6 |
103 54,5 |
5.23 |
103 54,7 |
163 33,6 |
146 02,7 |
|
|
|
|
|
|
|
|
5.9 |
73 15,3 |
43 39,8 |
85 32,1 |
5.24 |
86 20,1 |
124 41,9 |
89 50,6 |
|
|
|
|
|
|
|
|
5.10 |
101 20,0 |
86 34,6 |
84 25,7 |
5.25 |
128 31,9 |
55 20,0 |
124 59,2 |
|
|
|
|
|
|
|
|
5.11 |
44 00,2 |
78 11,3 |
163 50,3 |
5.26 |
76 32,5 |
99 58,7 |
124 24,1 |
|
|
|
|
|
|
|
|
5.12 |
26 13,8 |
116 02,4 |
83 52,4 |
5.27 |
91 03,1 |
61 36,6 |
34 41,3 |
|
|
|
|
|
|
|
|
5.13 |
88 58,6 |
33 02,5 |
105 55,1 |
5.28 |
38 51,5 |
96 19,6 |
35 57,8 |
|
|
|
|
|
|
|
|
5.14 |
50 01,3 |
97 32,4 |
44 35,2 |
5.29 |
43 35,1 |
109 00,7 |
96 49,2 |
|
|
|
|
|
|
|
|
5.15 |
137 11,2 |
124 10,6 |
110 22,3 |
5.30 |
22 22,6 |
69 53,9 |
132 10,3 |
|
|
|
|
|
|
|
|
12

2. Решение прямоугольных и четвертных сферических треугольников.
Прямоугольные – сферические треугольники у которых хотя бы один угол равен 90˚ .
Четвертные – сферические треугольники у которых хотя бы одна сторона = 90˚.
Расчетные формулы значительно упрощаются, если подставить в них значения тригонометрических функций для угла 90˚. sin 90˚= 1; cos 90˚= 0; ctg 90˚= 0.
Пример. В сферическом треугольнике заданы два угла и сторона между ними:
A = 90˚; b = 61˚07,8′; С=77˚10,4′.
Определить: a, B, с. Решение.
Основные формулы для нашего примера: cos B = – cos A cos C + sin A sin C cos b; ctgA sin C = ctg a sin b – cos C cos b;
ctg C sin A = ctg c sin b – cos A cos b.
Упростим формулы и выразим неизвестные элементы: cos B = sin A sin C cos b;
0 = ctg a sin b – cos C cos b => |
tg a = sin b/(cos C cos b) |
|
ctg C = ctg c sin b. |
=> |
tg c = sin b tg C |
Проверка: sin A / sin a = 1,03042; |
sin B / sin b = 1,03042; sin C / sin c = 1,03042. |
|
Ответ: a =103˚57,5′; B = 108˚43,1′; c =52˚14,5′.
Задания для индивидуальной работы.
В задачах № 6.1 ÷ 6.30 заданы два угла A, B и сторона с сферического треугольника. По данным таблицы 6, определить стороны a,b и угол C.
Таблица 6 – Варианты для выполнения индивидуальных заданий
№ |
с |
А |
В |
№ |
с |
А |
В |
6.1 |
90º00,0' |
105º36,2' |
73º57,6' |
6.16 |
90º |
118º44,0' |
97º41,4' |
6.2 |
36 32,4 |
90 |
45 35,1 |
6.17 |
54 18,7 |
90 |
95 26,5 |
6.3 |
58 43,8 |
76 56,9 |
90 |
6.18 |
90 39,5 |
93 04,1 |
90 |
6.4 |
52 51,5 |
90 |
64 07,1 |
6.19 |
129 46,6 |
90 |
14 21,2 |
6.5 |
90 |
137 01,0 |
111 50,0 |
6.20 |
90 |
88 38,1 |
105 44,5 |
6.6 |
45 49,0 |
90 |
46 32,3 |
6.21 |
58 17,7 |
90 |
139 10,4 |
6.7 |
61 27,5 |
104 23,3 |
90 |
6.22 |
142 45,4 |
49 57,9 |
90 |
6.8 |
65 31,4 |
90 |
85 57,0 |
6.23 |
145 40,0 |
100 23,7 |
90 |
6.9 |
90 |
124 50,3 |
82 17,1 |
6.24 |
64 46,2 |
90 |
127 48,4 |
6.10 |
99 30,4 |
110 23,1 |
90 |
6.25 |
90 |
2 16,5 |
101 16,6 |
6.11 |
90 |
164 44,2 |
37 53,7 |
6.26 |
90 |
54 23,2 |
95 01,2 |
6.12 |
104 55,6 |
90 |
70 06,0 |
6.27 |
66 03,2 |
90 |
96 21,1 |
6.13 |
90 |
152 58,7 |
55 21,6 |
6.28 |
133 01,7 |
90 |
86 45,0 |
6.14 |
75 38,9 |
38 35,0 |
90 |
6.29 |
29 02,6 |
59 38,5 |
90 |
6.15 |
77 18,4 |
90 |
128 16,2 |
6.30 |
90 |
156 43,3 |
47 56,4 |
13
ПРАКТИЧЕСКАЯ РАБОТА № 4.
1. Выбор оптимального маршрута судна.
Ортодромия (ДБК) – линия кратчайшего расстояния между двумя точками на поверхности земного шара, представляет собой наименьший из отрезков дуги большого круга, проходящей через эти точки.
Локсодромия – линия постоянного курса.
Целесообразность плавания по ортодромии определяется существенностью разности длин локсодромии Sл и ортодромии Dо, проложенных из пункта отхода в пункт прихода:
D Sл Dо .
Расчет длины локсодромии (Mercator sailing formula).
Алгоритм решения данной задачи включает следующие действия:
1. Вычисление разности широт (РШ, Δφ) – Δφ = φ2 – φ1.
Полученное значение Δφ переводим в угловые минуты (морские мили). 2. Определение разности долгот (РД, Δλ) – Δλ = λ2 – λ1.
Если |λ2 – λ1| > 180˚, то при вычислении Δλ берется дополнение абсолютной величины до 360˚, знак меняется на противоположный. Полученное значение Δλ переводим в угловые минуты (экваториальные мили).
3. Расчет разности меридиональных частей (РМЧ, MD) в экваториальных милях: MD = 3437,75 × ln [tg (45˚ + φ2/2) / tg (45˚ + φ1/2)].
Примечание: Знаки Δφ и MD должны совпадать.
4. Определение локсодромического курса КЛ:
KЛ' = arccos (MD / √(Δλ2 + MD2)).
при Δλ > 0 КЛ = КЛ′ ; при Δλ < 0 КЛ = 360˚ – КЛ′.
14
5. Расчет локсодромического расстояния SЛ (в морских милях):
при |
│cos КЛ│≥ 0,01 |
→ SЛ = Δφ / cos КЛ ; |
при |
│cos КЛ │< 0,01 |
→ SЛ = │Δλ│ cos φ1. |
Курс судна задается рулевому и учитывается при прокладке на карте с точностью до 0.5˚, но при вычислении локсодромического расстояния необходимо использовать значение КЛ с точностью не ниже 0,001˚. Практически берем то значение КЛ , которое появилось после вычисления на индикаторе микрокалькулятора.
Расчет длины ортодромии.
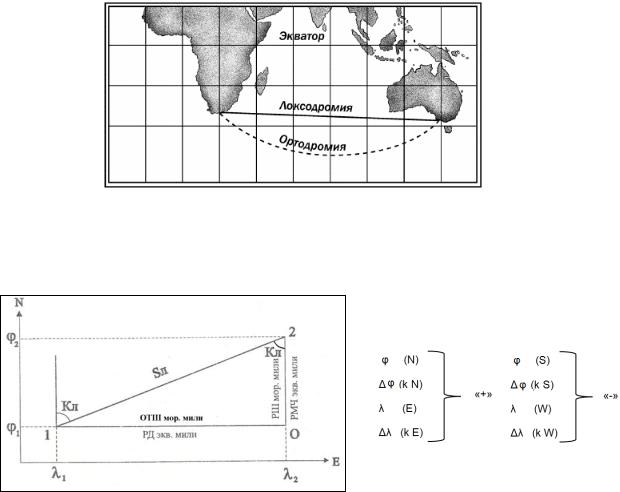
Расчет начального курса (Kн) и ортодромического расстояния (Dо) при плавании из точки А в точку В можно выполнить, рассмотрев сферический треугольник образованный пересечением меридианов проходящих через эти точки и дуги большого круга соединяющей точки А и В.
Пользуясь теоремами косинуса стороны и четырех рядом лежащих элементов,
величины Dо, Kн определяются следующим образом:
cos Dо = cos (90° – φA) · cos (90° – φB) + sin (90° – φA) · sin (90° – φB) · cos Δλ. ctg Kн' · sin | Δλ | = ctg (90° – φB) · sin (90° – φA) – cos (90° – φA) · cos Δλ.
Воспользуемся формулами приведения тригонометрических функций:
cos (90° – φA) = sin φA; sin (90° – φA) = cos φA; tg (90° – φA) = ctg φA. |
|
После преобразования получим конечные формулы для расчета величин Dо, Kн. |
|
Dо = arccos (sin A · sin B + cos A · cos B · cos Δλ). |
(4.1) |
Kн' = arcctg ( sin | Δλ | / (tg φB · cos φA – sin φA · cos Δλ. |
(4.2) |
Следует учитывать, что если Кн' получается отрицательным, то к нему необходимо прибавить 180˚.
–для получения Dо в морских милях, значение (4.1) умножаем на 60.
–для получения начального курса плавания по ортодромии Kн:
если Δλ > 0 (к Е), то: Кн = Кн'
если Δλ < 0 (к W), то: Кн = 360˚ – Кн'.
15
Задания для индивидуальной работы.
В задачах № 7.1 ÷ 7.30 по заданным координатам двух точек определить длину ортодромии Dо в морских милях и начальный курс плавания по ортодромии Kн.
Таблица 7 – Варианты для выполнения индивидуальных заданий
№ |
φ1 |
|
λ1 |
|
φ2 |
|
λ2 |
|
|
|
|
|
|
|
|
|
|
7.1 |
28°27' |
N |
095°28' |
W |
01°21' |
N |
134º11' |
E |
|
|
|
|
|
|
|
|
|
7.2 |
25 18 |
N |
087 29 |
E |
37 42 |
N |
041 18 |
W |
|
|
|
|
|
|
|
|
|
7.3 |
20 16 |
N |
120 02 |
W |
40 38 |
S |
016 35 |
W |
|
|
|
|
|
|
|
|
|
7.4 |
45 10 |
N |
067 56 |
W |
33 00 |
S |
079 25 |
E |
|
|
|
|
|
|
|
|
|
7.5 |
48 06 |
S |
106 41 |
W |
26 04 |
S |
007 40 |
E |
|
|
|
|
|
|
|
|
|
7.6 |
20 11 |
N |
125 59 |
W |
22 40 |
N |
045 34 |
E |
|
|
|
|
|
|
|
|
|
7.7 |
36 48 |
N |
099 42 |
W |
21 45 |
N |
035 40 |
E |
|
|
|
|
|
|
|
|
|
7.8 |
07 59 |
N |
131 50 |
W |
28 12 |
N |
124 57 |
E |
|
|
|
|
|
|
|
|
|
7.9 |
03 19 |
N |
040 50 |
W |
01 53 |
S |
058 25 |
E |
|
|
|
|
|
|
|
|
|
7.10 |
40 10 |
N |
175 03 |
W |
10 39 |
N |
047 39 |
E |
|
|
|
|
|
|
|
|
|
7.11 |
00 32 |
N |
053 31 |
W |
47 09 |
N |
108 46 |
E |
|
|
|
|
|
|
|
|
|
7.12 |
23 02 |
N |
081 29 |
W |
39 18 |
N |
044 01 |
E |
|
|
|
|
|
|
|
|
|
7.13 |
02 33 |
N |
048 46 |
W |
25 45 |
N |
132 20 |
E |
|
|
|
|
|
|
|
|
|
7.14 |
42 51 |
N |
108 21 |
W |
11 22 |
N |
019 09 |
E |
|
|
|
|
|
|
|
|
|
7.15 |
07 24 |
S |
091 24 |
W |
29 16 |
N |
056 40 |
E |
|
|
|
|
|
|
|
|
|
7.16 |
36 09 |
S |
052 39 |
W |
23 43 |
N |
016 15 |
E |
|
|
|
|
|
|
|
|
|
7.17 |
19 26 |
S |
087 04 |
W |
42 40 |
S |
007 05 |
E |
|
|
|
|
|
|
|
|
|
7.18 |
15 13 |
S |
166 54 |
W |
23 02 |
S |
161 35 |
E |
|
|
|
|
|
|
|
|
|
7.19 |
48 48 |
S |
143 09 |
E |
15 42 |
S |
095 16 |
E |
|
|
|
|
|
|
|
|
|
7.20 |
36 05 |
S |
128 50 |
E |
16 40 |
S |
040 26 |
E |
|
|
|
|
|
|
|
|
|
7.21 |
46 35 |
S |
095 16 |
E |
35 53 |
S |
029 34 |
E |
|
|
|
|
|
|
|
|
|
7.22 |
34 48 |
S |
039 22 |
W |
21 47 |
S |
029 52 |
E |
|
|
|
|
|
|
|
|
|
7.23 |
17 26 |
N |
021 05 |
E |
31 41 |
N |
039 16 |
W |
|
|
|
|
|
|
|
|
|
7.24 |
05 25 |
N |
142 05 |
W |
30 19 |
S |
106 57 |
W |
|
|
|
|
|
|
|
|
|
7.25 |
02 27 |
N |
098 01 |
E |
46 59 |
S |
132 00 |
W |
|
|
|
|
|
|
|
|
|
7.26 |
10 38 |
S |
093 32 |
E |
37 18 |
S |
099 23 |
W |
|
|
|
|
|
|
|
|
|
7.27 |
35 34 |
S |
005 06 |
E |
24 41 |
S |
104 50 |
W |
|
|
|
|
|
|
|
|
|
7.28 |
35 23 |
S |
019 48 |
E |
26 02 |
S |
120 02 |
W |
|
|
|
|
|
|
|
|
|
7.29 |
23 23 |
S |
110 58 |
E |
21 41 |
S |
119 02 |
W |
|
|
|
|
|
|
|
|
|
7.30 |
44 59 |
S |
007 20 |
W |
20 18 |
S |
002 00 |
W |
|
|
|
|
|
|
|
|
|
16
ПРАКТИЧЕСКАЯ РАБОТА № 5.
Обработка равноточных и неравноточных наблюдений.
В зависимости от условий измерений, наблюдения делятся на равноточные и неравноточные.
Измерения выполненные одним наблюдателем с помощью одного и того же прибора, одним методом, в течении короткого промежутка времени и при одинаковых внешних условиях называются равноточными.
Всем измерениям присущи погрешности:
–систематические;
–случайные;
–промахи.
Систематические погрешности изменяют свой знак и величину по определенному закону. Их влияние можно исключить, введя поправки в измерения или в прибор.
После исключения влияния систематических погрешностей, определяют и исключают промахи.
Промахом называется грубая ошибка, величина которой заметно превышает ошибки измерений или вычислений при данных условиях.
Случайные погрешности изменяют свой знак и величину от наблюдения к наблюдению без каких-либо известных закономерностей. Определить и предугадать конкретное значение случайной погрешности невозможно. Оценить их величину и уменьшить влияние на принимаемое для дальнейших расчетов значение измеряемого параметра можно путем соответствующей обработки серии равноточных измерений.
Наиболее исчерпывающе случайные погрешности описываются законом распределения. На практике обычно ограничиваются их числовыми характеристиками: математическим ожиданием и дисперсией или средней квадратической погрешностью (СКП).
1.Обработка равноточных наблюдений.
1.Обработку равноточных наблюдений начинаем с исключения из серии измерений
промахов.
Для этого исключим из серии измерений результат x′, подозреваемый на промах (наиболее отличающийся от других). По оставшимся измерениям определяем размах:
R = xmax – xmin. |
(5.1) |
Вычисляем разность x′ – x”,
где: x” – ближайшее к x′ измерение – xmax или xmin.
Проверка x′ на принадлежность к промаху производится с помощью неравенства:
│x′ - x”│ > Q×R.
17
Если неравенство выполняется, то x′ – промах. Исключаем его из результатов измерений.
В противном случае отброшенное измерение оставляем в серии и приступаем к вычислению числовых характеристик. Численное значение коэффициента Q выбирается из таблицы Приложение 2 по числу измерений n – 1, оставшихся после исключения подозреваемого на промах значения x′.
После того, как промах определен и исключен, необходимо проверить на промах измерение, наиболее отличающееся от оставшихся. Процедура повторяется до тех пор, пока не окажется, что наиболее отличающееся от остальных измерение не является промахом.
2. Проведем оценку математического ожидания. Наиболее точной из всех возможных оценок является
результатов измерений: |
|
1 |
n |
|
|
x |
|
||
|
|
|
x , |
|
|
|
|||
|
o |
n i 1 |
i |
|
|
|
|
|
|
где: xi – i-тое значение навигационного параметра; n – число измерений в серии.
среднее арифметическое из
(5.2)
Когда результаты измерений выражаются многозначными числами, среднее арифметическое целесообразно вычислить по формуле:
xo xу |
1 |
n |
|
(x x |
|
|
(5.3) |
|
|
|
у |
), |
|||
|
|
|
|||||
|
n i |
1 |
i |
|
|
||
|
|
|
|
|
|||
где: xу – удобно выбранное число.
3. Рассчитаем среднюю квадратическую погрешность (mx) одного измерения.
Мы рассматриваем равноточные наблюдения, следовательно mx1 = mx2 = ……..= mx.
а). по отклонениям от среднего арифметического (формула Бесселя):
где: vi = xi – x0.
mx |
|
|
1 |
|
|
|
(5.4) |
||
|
|
n 1 |
|||||||
|
|
|
|
|
|||||
б). по размаху R = xmax – xmin : |
|
|
|
|
|
|
|
|
|
m хmax - хmin |
(5.5) |
||||||||
х |
|
|
|
n |
|
||||
|
|
|
|
|
|||||
4. Рассчитаем СКП среднего арифметического: |
|
||||||||
mx |
|
mх |
(5.6) |
||||||
|
|
|
|
|
|
|
|||
|
|
|
n |
||||||
o |
|
|
|
|
|
||||
|
|
|
|
|
|
||||
Предельная погрешность измерений, подчиняющихся нормальному закону |
|||||||||
распределения, вычисляется по формуле: |
|
|
|
|
|
|
|
|
|
Дпр = ± 3 × mх. |
(5.7) |
||||||||
18
