Лекция № 8.Теорема Кронекера-Капели. Решение систем линейных уравнений методом Гаусса. Обратная матрица и способы ее нахождения. Матричный способ решения систем линейных уравнений.

Теорема (Кронекера – Капели) Чтобы система линейных уравнений была

совместной, необходимо и достаточно чтобы ранги основной и расширенной матриц были равны.

Общим способом решения системы линейных уравнений

(1)

является метод Гаусса. Суть его состоит в том, чтобы данную систему линейных уравнений преобразовать к эквивалентной системе, максимально ее упростив. Можно показать, что такие преобразования как: перестановка местами любых двух уравнений в системе; умножение любого уравнения на любое число ; умножение любого уравнения системы на любое число и прибавление его к любому другому уравнению системы, не изменяют множества решений системы, т.е. приводят к эквивалентной системе. Заметим, что перечисленные выше преобразования уравнений системы (1) фактически сводятся к элементарным преобразованиям матрици, из которых построена расширенная матрица системы (1). Поэтому преобразуем расширенную матрицук ступенчатому виду. В результате преобразований возможны следующие три случая.

1. При некотором преобразовании получаем строку матрицы, в которой все элементы до черты равны нулю, а элемент после черты отличен от нуля. Это говорит о том, что в системе есть уравнение

, ,

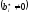которое не имеет решений. Следовательно, в этом случае система несовместна.

2. После отбрасывания нулевых строк, если таковые есть, получим квадратную матрицу треугольного вида . В ней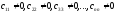. По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид.

Из последнего уравнения находим . Подставляя это значениев предпоследнее уравнение, найдем. Затем, подставив найденные значенияив предыдущее уравнение, получим. Продолжая далее этот процесс, получим.

Таким образом, в этом случае система (1) имеет единственное решение. Такие системы называют определенными.

3. После отбрасывания нулевых строк, если таковые есть, получим матрицу ступенчатого вида . По этой матрице можно записать систему уравнений, равносильную системе (1). Она имеет вид

.

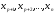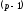Не ограничивая общности можно считать, что . Выразив из последнего уравнения системычерез, получим. Затем подставим найденное значениев предыдущее уравнение и выразимчерез. Подставивв предыдущее уравнение, выразимчерез. И так далее. Послешагов мы выразимчерези получим общее решение системы (1). Ясно, что в общем решении содержится бесконечно много решений системы (1), так как переменныемогут принимать любые значения. Их называют свободными переменными. Придавая свободным переменным конкретные значения мы будем получать различные частные решения системы (1). Системы уравнений, имеющие бесконечно много решений, называют неопределенными.

Легко видеть, что если система (1) является однородной, то она всегда совместна, так как имеет решение . В этом случае никакое из элементарных преобразований не меняет матрицу свободных членов. Поэтому при решении однородных систем методом Гаусса обычно приводят к ступенчатому виду матрицу системы, а не расширенную матрицу системы.

Пусть имеем квадратную матрицу . Обратной для нее называют такую матрицу, которая удовлетворяет условию.

Легко заметить, что не всякая матрица имеет обратную. Действительно, по свойству определителей с учетом определения обратной матрицы должны иметь . А поскольку, то ни один из определителейине может равняться нулю. Значит необходимым условием существования обратной матрицы для матрицыявляется ее невырожденность. Можно доказать, что это условие является и достаточным. Для этого просто укажем алгоритм получения обратной матрицы для любой невырожденной матрицы.

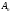1. Вычисляем .

2. Для каждого элемента матрицы вычисляем алгебраические дополнения.

3. Составляем из этих алгебраических дополнений матрицу .

4. Транспонируем матрицу , получая матрицу, называемую присоединенной к матрице.

5. Умножаем матрицу на число.

Полученная в результате матрица и будет обратной для. В этом можно убедиться проверкой.

Существует другой способ нахождения обратной матрицы – способ перегонки. Суть его в следующем. Пусть имеем невырожденную квадратную матрицу . Припишем к данной матрицесправа единичную матрицу, т.е. построим матрицуи с помощью элементарных преобразований над матрицами«перегоним» матрицу , стоящую справа от черты, на место матрицы, стоящей слева от черты. Тогда матрица, получившаяся справа от черты и будет обратной для. 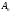В этом можно убедиться проверкой.

Если в системе (1) число уравнений совпадает с числом неизвестных , а матрица системыявляется невырожденной, то кроме метода Гаусса можно также применить матричный метод. Суть его состоит в следующем. Находим матрицу, обратную для матрицы, и умножаем ее слева на матричное уравнение системы. Получаем. Учитывая, что, а, приходим к уравнению, которое и дает нам искомое решение (в матричном виде). Очевидно, что этот метод можно применять только для решения систем с невырожденной матрицей. В противном случае для матрицынет обратной.