
- •1.1 Матрицы. Виды матриц. Операции над матрицами. Определители квадратных матриц и их свойства. Собственные числа матрицы.
- •Лекция № 7Элементарные преобразования матриц. Ранг матрицы. Матричная запись системы линейных уравнений. Решение систем линейных уравнений методом Крамера.
- •Лекция № 8.Теорема Кронекера-Капели. Решение систем линейных уравнений методом Гаусса. Обратная матрица и способы ее нахождения. Матричный способ решения систем линейных уравнений.
Лекция № 7Элементарные преобразования матриц. Ранг матрицы. Матричная запись системы линейных уравнений. Решение систем линейных уравнений методом Крамера.
Пусть имеем
матрицу
 .
Рассматривая элементы каждой строки
как координаты
.
Рассматривая элементы каждой строки
как координаты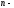 мерных
векторов
мерных
векторов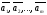 соответственно, матрицу
соответственно, матрицу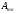 можно записать в виде матрицы-столбца
можно записать в виде матрицы-столбца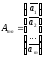 .
Наибольшее число линейно независимых
векторов во множестве {
.
Наибольшее число линейно независимых
векторов во множестве { }
называют строчным рангом матрицы
}
называют строчным рангом матрицы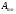 .
.
Если же в
матрице
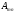 элементы каждого столбца рассматривать
как координаты
элементы каждого столбца рассматривать
как координаты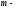 мерных
векторов
мерных
векторов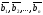 ,
то матрицу
,
то матрицу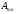 можно записать в виде матрицы-строки
можно записать в виде матрицы-строки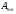 =(
=(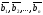 ).
Наибольшее число линейно независимых
векторов во множестве {
).
Наибольшее число линейно независимых
векторов во множестве {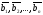 }
называют столбцовым рангом матрицы
}
называют столбцовым рангом матрицы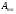 .
Можно доказать, что строчный и столбцовый
ранги любой матрицы равны. Их общее
значение называют рангом матрицы
.
Можно доказать, что строчный и столбцовый
ранги любой матрицы равны. Их общее
значение называют рангом матрицы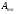 и обозначают символом
и обозначают символом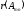 .
.
Однако находить ранг матрицы по определению часто бывает неудобно из-за трудоемкости. Обычно для определения ранга матрицы ее преобразовывают к ступенчатому виду, который сразу позволяет определить линейную зависимость или независимость ее строк или столбцов.
Матрицей
ступенчатого вида называют матрицу
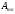 ,
обладающую свойством: если
,
обладающую свойством: если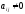 - первый ненулевой элемент
- первый ненулевой элемент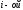 строки
строки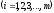 ,
то все элементы матрицы, стоящие ниже
и левее
,
то все элементы матрицы, стоящие ниже
и левее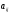 ,
равны нулю (т.е
,
равны нулю (т.е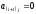 ,
,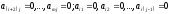 при всех
при всех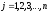 ).
При этом элементы
).
При этом элементы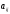 называют угловыми. Например, матрица
называют угловыми. Например, матрица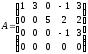 является матрицей ступенчатого вида.
В первой строке первым отличным от нуля
элементом является
является матрицей ступенчатого вида.
В первой строке первым отличным от нуля
элементом является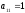 .
Все элементы, стоящие ниже его равны
нулю:
.
Все элементы, стоящие ниже его равны
нулю: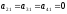 .
Во второй строке первым отличным от
нуля элементом является
.
Во второй строке первым отличным от
нуля элементом является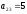 .
Все элементы, стоящие ниже и левее равны
нулю:
.
Все элементы, стоящие ниже и левее равны
нулю: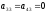 ,
,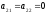 .
В третьей строке первый отличный от
нуля элемент
.
В третьей строке первый отличный от
нуля элемент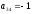 ,
а
,
а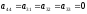 .
В четвертой строке все элементы нулевые.
Таким образом, угловыми элементами
матрицы
.
В четвертой строке все элементы нулевые.
Таким образом, угловыми элементами
матрицы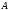 ,
имеющей ступенчатый вид, являются
,
имеющей ступенчатый вид, являются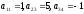 .
Матрица
.
Матрица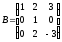 не является матрицей ступенчатого вида,
так как для первого отличного от нуля
элемента второй строки
не является матрицей ступенчатого вида,
так как для первого отличного от нуля
элемента второй строки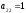 элемент
элемент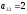 ,
стоящий ниже, отличен от нуля.
,
стоящий ниже, отличен от нуля.
Рассмотрим преобразования, не меняющие ранга матрицы, т.е. не меняющие линейной зависимости (независимости) строк или столбцов матрицы. К ним относятся следующие преобразования, которые называют элементарными:
отбрасывание нулевой строки (столбца);
изменение порядка строк (столбцов);
транспонирование матрицы;
умножение всех элементов строки (столбца) на любое число
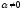 ;
;умножение всех элементов одной строки (столбца) на любое число и прибавление их к соответствующим элементам другой строки (столбца).
Можно доказать, что с помощью перечисленных выше преобразований любая матрица приводится к ступенчатому виду. При этом ее ранг будет равен числу угловых элементов матрицы.
Систему,
состоящую из
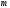 уравнений с
уравнений с неизвестными
неизвестными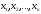 вида
вида
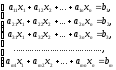 (1)
(1)
называют
системой линейных уравнений. В ней
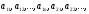
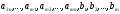 - заданные числа. Решением такой системы
называется набор чисел
- заданные числа. Решением такой системы
называется набор чисел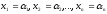 ,
при подстановке которых в систему,
каждое из уравнений превращается в
верное равенство. Решить систему
уравнений (1) – значит найти множество
всех решений или доказать, что система
не имеет решений. Система, имеющая хотя
бы одно решение, называется совместной;
в противном случае – несовместной.
,
при подстановке которых в систему,
каждое из уравнений превращается в
верное равенство. Решить систему
уравнений (1) – значит найти множество
всех решений или доказать, что система
не имеет решений. Система, имеющая хотя
бы одно решение, называется совместной;
в противном случае – несовместной.
Две системы линейных уравнений называют эквивалентными, если множества решений этих систем совпадают. В противном случае системы называют неэквивалентными.
Если
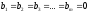 ,
то систему (1) называют однородной; в
противном случае (т.е. если хотя бы одно
из чисел
,
то систему (1) называют однородной; в
противном случае (т.е. если хотя бы одно
из чисел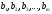 не равно нулю) – неоднородной.
не равно нулю) – неоднородной.
Матрицу
 называют матрицей системы (1); матрицу
называют матрицей системы (1); матрицу называют расширенной матрицей системы
(1); матрицу
называют расширенной матрицей системы
(1); матрицу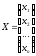 называют матрицей неизвестных, а матрицу
называют матрицей неизвестных, а матрицу - матрицей свободных членов. Нетрудно
заметить, что систему (1) можно записать
в матричной форме в виде
- матрицей свободных членов. Нетрудно
заметить, что систему (1) можно записать
в матричной форме в виде
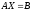 . (2)
. (2)
Если в системе (1) число
неизвестных совпадает с числом уравнений
(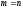 )
и
)
и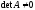 ,
то систему можно решить методом Крамера
по формулам
,
то систему можно решить методом Крамера
по формулам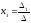 ,
,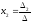 ,
…,
,
…,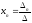 ,
где
,
где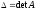 ,
,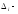 определители,
полученные из
определители,
полученные из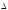 заменой
заменой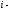 го столбца столбцом свободных членов
го столбца столбцом свободных членов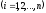 .
.
