Ряды с неотрицательными членами

При изучении знакопостоянных рядов ограничимся рассмотрением рядов с неотрицательными членами, т.к. при простом умножении на –1 из этих рядов можно получить ряды с отрицательными членами.

Теорема. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы частные суммы ряда были ограничены, т.е. последовательность частичных сумм была ограничена.

Доказательство.

Необходимость. Пусть ряд сходится, тогда последовательность его частичных сумм сходится. А сходящаяся последовательность – ограничена.

Достаточность. В силу того, что последовательность частичных сумм ряда является ограниченной и монотонной, то она сходится в силу теоремы о достаточном признаке существования предела (Монотонная ограниченная последовательность имеет конечный предел).

Признаки сравнения рядов

Теорема. Если и ‑‑ числовые ряды с положительными членами, причем при любомn, то из сходимости ряда следует сходимость ряда , а из расходимости ряда следует расходимость ряда .

Доказательство. Обозначим через и частичные суммы рядов и соответственно. По условию теоремы ряд сходится, поэтому все его частичные суммы ограничены, т.е. при всех , где– некоторое число. А так как, по условию,, то. Значит частичные суммы ряда тоже ограничены, а этого уже достаточно для сходимости ряда.

В некоторых случаях ряд называется мажорантой ряда , а ряд ‑‑ минорантойряда . Тогда теорему можно сформулировать следующим образом:

‑‑ Если мажоранта сходится, то и миноранта сходится.

‑‑ Если миноранта расходится, то и мажоранта расходится.

Пример . Исследовать на сходимость ряд .

Решение. Так как , а гармонический рядрасходится, то расходится и ряд.

Пример . Исследовать на сходимость ряд

Решение. В силу того, что , а рядсходится (это убывающая геометрическая прогрессия), то рядтоже сходится.

Теорема. Если и существует предел, где – число, отличное от нуля, то ряды и сходятся или расходятся одновременно.

Необходимо заметить, что оба рассмотренных признака имеют один и тот же недостаток: для исследования сходимости некоторого положительного ряда с помощью данных признаков необходимо подобрать другой ряд, сходимость (или расходимость) которого известна. Общих методов для нахождения таких рядов нет. Все зависит от интуиции, то есть от обширности запаса «эталонных» рядов у исследователя.

Признак Даламбера

(Жан Лерон Даламбер (1717–1783) –французский математик)

Теорема. Если существует предел , то приряд сходится, а при– расходится.

Если , то на вопрос о сходимости ряда остается открытым.

Доказательство. По определению предела последовательности существует номер, что для всехвыполняется неравенство

.

( )

Пусть , тогдаможно взять таким, что. Из неравенства ( . ) имеем

, или для всех. Получаем систему неравенств.

Отсюда, члены ряда, начиная с , меньше соответствующих членов убывающей геометрической прогрессии. Следовательно, ряд сходится.

Пусть теперь . Возьмем такое, что. Тогда из левого неравенства ( . ) следует, чтодля всех, т.е. члены ряда, начиная с-го, возрастают, поэтому предел общего члена ряда не равен нулю, значит – ряд расходится.

Пример . . Определить сходимость ряда .

Решение.

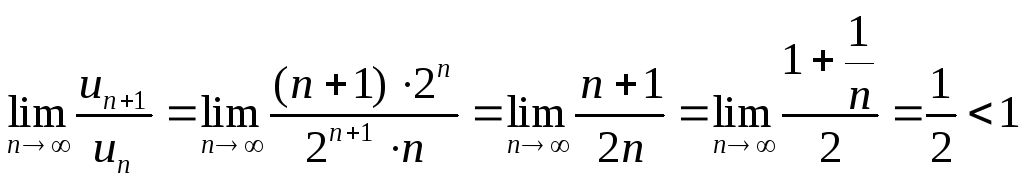. Следовательно, ряд сходится по признаку Даламбера.

Пример . . Определить сходимость ряда .

Решение.

, ряд сходится.