Ряды Основные определения

Определение. Сумма членов бесконечной числовой последовательности называетсячисловым рядом

.

( )

При этом числа будем называть членами ряда, аu_n – общим членом ряда.

Определение. Суммы ,n называются частными или частичными суммами ряда.

Очевидно, что частичные суммы образуют числовую последовательность: .

Определение. Ряд называетсясходящимся, если сходится последовательность его частных сумм, т.е.

( )

В противном случае ряд называется расходящимся. Число называетсясуммой ряда.

Пример .1. Рассмотрим ряд, составленный из членов бесконечной геометрической прогрессии:

( )

Частичная сумма этого ряда является суммойчленов геометрической прогрессии:

==, при.

Если , то, то

,

то ряд сходится и его сумма равняется .

Несложно проверить, что при ряд расходится.

Пример .2. Рассмотрим ряд .

Преобразуем . Отсюда,

.

После раскрытия скобок, все слагаемые, кроме первого и последнего, взаимно уничтожаются. Получим .

Поэтому . Значит, ряд сходится и его сумма равна единице.

Свойства рядов.

Свойство 1. Отбрасывание конечного числа членов ряда не влияет на его сходимость (или расходимость).

Действительно, все частичные суммы ряда, начиная с некоторой, изменятся на одно и то же постоянное число, равное сумме отбрасываемых членов.

Свойство 2. Если ряд сходится и его сумма равна, то рядтоже сходится, и его сумма равна.

Пусть ,. Тогда. Но по условию.

Поэтому , что и требовалось доказать.

Свойство 3. Если ряды исходятся и их суммы равны соответственнои, то рядтоже сходится, причем его сумма равна.

Пусть ,,частичные суммы рядов,исоответственно.

Если , а, то существует предел, т.е. ряд сходится и его сумма равняется.

Разность двух сходящихся рядов также будет сходящимся рядом.

Сумма сходящегося и расходящегося рядов будет расходящимся рядом.

Необходимый признак сходимости ряда

Свойство 4. Общий член сходящегося ряда стремится к нулю при, т.е..

Пусть ряд сходится и его сумма равна , т.е.. Очевидно, что, кроме того. Поэтому.

Здесь установили только необходимое условие сходимости. Если оно не выполняется, то ряд заведомо расходится.

Пример .3. Исследовать сходимость ряда .

Если общий член ряда не стремится к нулю, то ряд точно расходится.

Найдем 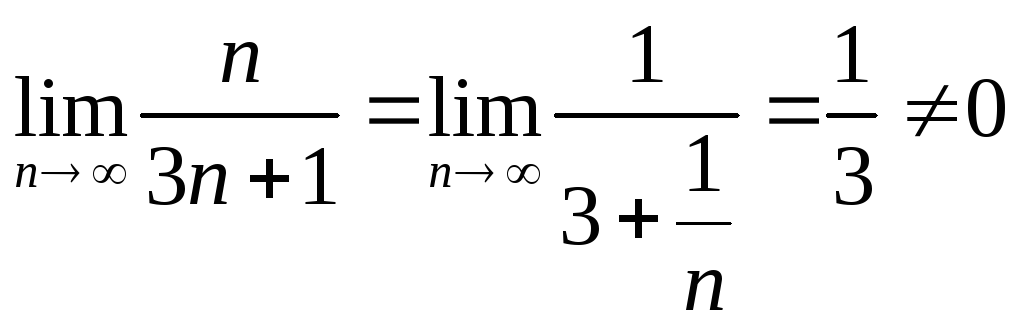‑‑ необходимый признак сходимости не выполняется, значит ряд расходится.

Пример .4. Исследовать сходимость (гармонического) ряда .

Для гармонического ряда выполняется необходимое условие сходимости, т.е. . Покажем, что он все же расходится. Будем доказывать от противного. Предположим, что ряд сходится и. Тогда, очевидно, и, следовательно,. Однако, т.е., а это противоречит условию сходимости гармонического ряда. Полученное противоречие означает, что наше предположение о сходимости гармонического ряда неверно.

Свойство 5. Если ряд сходится, то последовательность его частных сумм ограничена.

Однако, этот признак также не является достаточным.

Например, ряд расходится, т.к. расходится последовательность его частных сумм в силу того, что

Однако, при этом последовательность частных сумм ограничена, т.к. при любомn.