Курсач по ТАУ. Вариант_13.2011

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Чувашский государственный университет им. И.Н.Ульянова»

Кафедра ТОЭ

Курсовая работа

по теории автоматического регулирования

Вариант 13

Выполнила: студентка гр. ЭЭ-21-08

Елисеева В.В.

Проверил: к.т.н., старший преподаватель

Мочалов М.Ю.

г. Чебоксары - 2011 г.

1. Линеаризация

1.1 Постройте линеаризованную модель для звена, которое описывается нелинейным дифференциальным уравнением (значения Т=2.1, q₂=0.5, q₁=1.2, k=0.5):

В номинальном режиме установившееся значение у=у₀=0.5.

Большинство систем управления описывается нелинейными ДУ, но во многих случаях их можно линеаризовать, т.е. заменить исходные нелинейные уравнения на линейные.

Запишем для нашего случая уравнение динамики:

Этому уравнению соответствует следующее уравнение статики, которое определяется при постоянных входных воздействиях х₀ (все производные образуются в 0):

В основе линеаризации нелинейных уравнений лежит предположение о том, что в исследуемом динамическом процессе переменные изменяются так, что их отклонения от установившихся значений остаются все время достаточно малыми. Это позволяет производить линеаризацию, разлагая нелинейные функции, входящие в уравнения, в ряд Тейлора.

Разложив нашу функцию получим:

Вычтем из полученного уравнения почленно уравнение статики, получим искомое линеаризованное уравнение динамики данного звена:

1.2 Определите установившееся значение х=х_0.

Уравнение установившегося режима выглядит следующим образом:

Выразим из этого уравнения х_0:

1.3 Постройте передаточную функцию линеаризованного звена. Как называется такое звено?

Передаточная функция звена W(р) определяется как отношение изображения Лапласа выходных и входных величин при нулевых начальных условиях.

В нашем случае чтобы построить передаточную функцию необходимо сначала подставить вместо дифференцирования оператор р. Тогда уравнение примет следующий вид:

Уравнению соответствует следующая передаточная функция:

Видим что это апериодическое звено первого порядка. Приведем к требуемому виду:

Передаточная функции имеет вид:

1.4 Найдите импульсную характеристику (весовую функцию) этого звена.

Функция веса (весовая функция) представляет собой реакцию звена на δ-функцию (единичная импульсная функция).

Для того чтобы определить весовую функцию воспользуемся теоремой разложения. В нашем случае имеется один корень, поэтому импульсная функция будет иметь вид:

Корень нашего уравнения: р=-0.81. Найдем все составляющие:

Построим эту функцию:

1.5 Решив полученное линейное дифференциальное уравнение, найдите переходный процесс на выходе линеаризованного звена при ступенчатом входном сигнале х(t)=1(t).

Переходная функция или переходная характеристика представляет собой переходной процесс на выходе звена, возникающий при подаче на его вход единичного воздействия.

Ранее была найдена весовая функция. Переходную функцию можно определить по известной весовой, воспользуемся данным методом.

Начальные условия: у(0)=0. Определим С по этому условию в момент времени t=0.

Тогда запишем полученную весовую функцию:

2. Разомкнутые системы

2.1 Определите, какие простейшие звенья можно выделить в составе звена с передаточной функцией (значения коэффициентов а₁=-0,7, а₀=1.4, b₂=1.6, b₁=1.3, b₀=0.8):

Подставив свои данные получим следующую передаточную функцию:

Попробуем разложить функцию так, чтобы можно было выделить простейшие звенья:

Получилось что наша передаточная функция состоит из двух звеньев: форсирующего звена первого порядка (звено получается в результате различных параллельных соединений пропорционального и дифференцирующего или инерционного звеньев) и колебательного звена.

2.2 Чему равен коэффициент усиления этого звена в установившемся режиме?

В установившемся режиме все производные равны 0, поэтому коэффициент усиления равен передаточной функции W(0). В установившемся режиме р=0.

2.3 Является ли звено устойчивым? Почему?

Устойчивость является одним из необходимых условий, обеспечивающих нормальное функционирование автоматических систем.

Устойчивость систем АУ – свойство системы возвращаться в исходное состояние равновесия после прекращения изменения воздействия, которое вывело систему из этого состояния.

Для устойчивой линейной системы необходимо и достаточно чтобы действительные части всех корней характеристического уравнения системы были отрицательными или чтобы все корни характеристического уравнения системы располагались в левой части комплексной плоскости.

Найдем корни характеристического уравнения:

Видим, что вещественные корни уравнения отрицательны, т.е. корни лежат в левой полуплоскости и поэтому наша система устойчива.

2.4 Является ли звено минимально-фазовым?

В случае, если корни числителя и знаменателя передаточной функции W(p) звена лежат в левой полуплоскости, такое звено называется минимально-фазовым. Этим звеньям присущи меньшие по абсолютной величине фазовые сдвиги по сравнению со звеньями, у которых это условие не выполняется.

Определим корни числителя нашей передаточной функции (уже определили, что корни знаменателя – отрицательны):

Отсюда видим, что звено не является минимально-фазовым.

2.5 Постройте асимптотическую ЛАФЧХ этого звена.

Мы получили три простейших звена, которые соединены между собой последовательно (т.к передаточная функция – это произведение этих простейших звеньев).

Построим асимптотическую ЛАЧХ:

Найдем сопрягающие частоты и пронумеруем их в порядке возрастания: ω₁=0.71; ω₂=2.

При построении асимптотической ЛАЧХ при частотах меньше сопрягающей частоты ω_c под корнем оставляют только единицу (пренебрегая другими слагаемыми), при частотах больше сопрягающей частоты оставляют слагаемые с наивысшей степенью ω.

При ω< ω₁:

При ω₁<ω< ω₂:

При ω> ω₂:

_{Асимптотическая ЛАЧХ:}

_{Точная ЛАЧХ:}

_{2.6 Какой наклон имеет ЛАЧХ на нулевой частоте? На больших частотах? Почему?}

_{Наклон на нулевой частоте определяется только дифференцирующим и интегрирующим звеньями. Если имеется m дифференцирующих звеньев, то наклон будет 20m дБ/дек. Если есть n интегрирующих звеньев, то наклон : -20n дБ/дек.}

_{Позиционные звенья имеют нулевой наклон.}

_{Наклон на высоких частотах: -20m Дб/дек, где m – разность степеней знаменателя и числителя передаточной функции.}

_{В нашем случае, наклона на нулевой частоте нет, т.к. наше звено – позиционное.}

_{Наклон на высоких частотах: -20 Дб/дек, т.к. степень знаменателя вторая, а числителя – первая.}

_{2.7 Запишите модель этого звена в виде дифференциального уравнения.}

_{Наша передаточная функция выглядит следующим образом:}

_{Запишем ее в виде дифференциального уравнения:}

_{2.8 Запишите модель этого звена в пространстве состояний.}

_{Переменными состояния динамической системы с выходом у называются независимые переменные хi(t) такие, что значения выходных переменных y(t) в произвольный момент времени t1≥t0 однозначно определяется значениями xi(t0). Таким образом, чтобы найти реакцию системы на любой известный входной сигнал достаточно знать ее вектор состояния в начальный момент времени.}

_{Модель в пространстве состояния – это система дифференциальных уравнений первого порядка, к которой добавлены связи вектора состояния с входом и выходом системы.}

_{Для одномерных систем имеющих один вход и один выход существует простой способ построения модели в пространстве состояния по передаточной функции.}

_{Представим:}

Передаточная функция W₁(p) соответствует уравнению:

Передаточная функция W₂(р) соответствует уравнению:

Вводя переменные стояния: х₁=z, х₂=, и учитывая связь между ними: х₂=, получим систему:

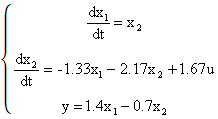
Данная система записывается в форме модели пространстве состояний с матрицами:

_{2.9 Постройте переходную характеристику этого звена.}

Воспользуемся теоремой разложения.

Корни нашего уравнения комплексно сопряженные:. Найдем все составляющие:

Мы нашли весовую функцию. Переходную функцию можно определить по известной весовой, воспользуемся данным методом.

_{3. Замкнутые системы}

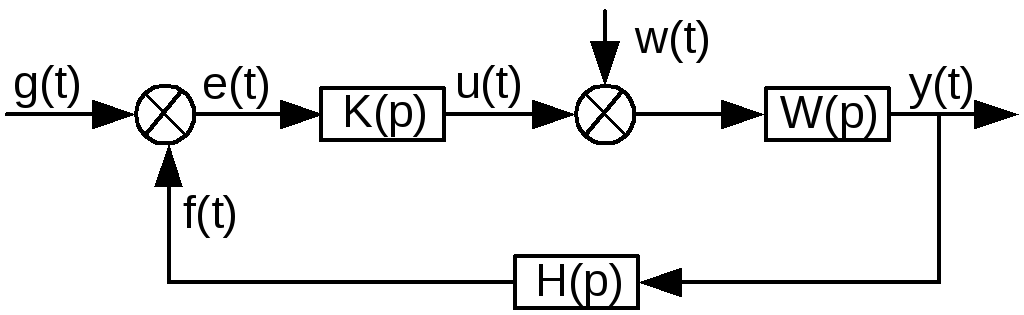
_{3.1 Пусть объект управления имеет передаточную функцию W(p), регулятор – передаточную функцю K(p), а измерительная система – передаточную функцию H(p). Нарисуйте типовую блок-схему системы автоматического регулирования, обозначив задающий сигнал g(t), сигнал управления u(t), регулируемый сигнал y(t), внешнее возмущение w(t), сигнал обратной связи f(t), сигнал ошибки e(t).}

_{3.2 Предположив, что К(р)=к=const и Н(р)=h=const, постройте передаточные функции (ПФ):}

_{-G(p) от входа g(t) к выходу y(t);}

_{-Gu(p) от входа g(t) к выходу u(t);}

_{-Gе(p) от входа g(t) к выходу е(t);}

_{-Gfe(p) от входа w(t) к выходу e(t);}

_{ПФ G(p) от входа g(t) к выходу y(t) – это передаточная функция всей замкнутой системы. Она состоит из ПФ по задающему и по возмущающему воздействию. Найдем и построим отдельно эти передаточные функции:}

_{- ПФ по задающему воздействию:}

_{- ПФ по возмущающему воздействию:}

_{ПФ Gu(p) от входа g(t) к выходу u(t):}

_{ПФ Ge(p) от входа g(t) к выходу e(t):}

_{ПФ Gfe(p) от входа w(t) к выходу e(t):}

_{3.3 Используя критерий Гурвица, определите, при каких значениях k и h замкнутая система устойчива.}

_{По критерию Гурвица, для того чтобы система была устойчива необходимо, чтобы все коэффициенты замкнутой системы были положительны. Характеристическое уравнение имеет вид:}

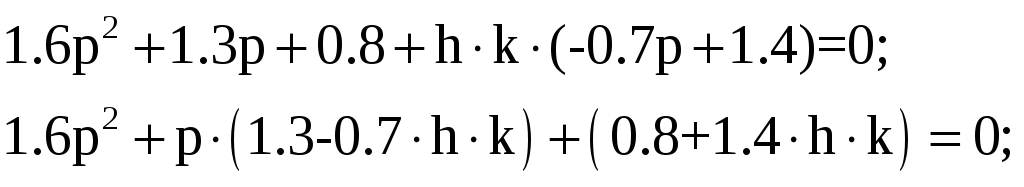
_{Согласно критерию Гурвица, необходимо, чтобы все коэффициенты и определители были положительными. Т.к. мы имеем уравнение второго порядка, то необходимо, чтобы положительными были коэффициенты.}

_{Получим систему:}

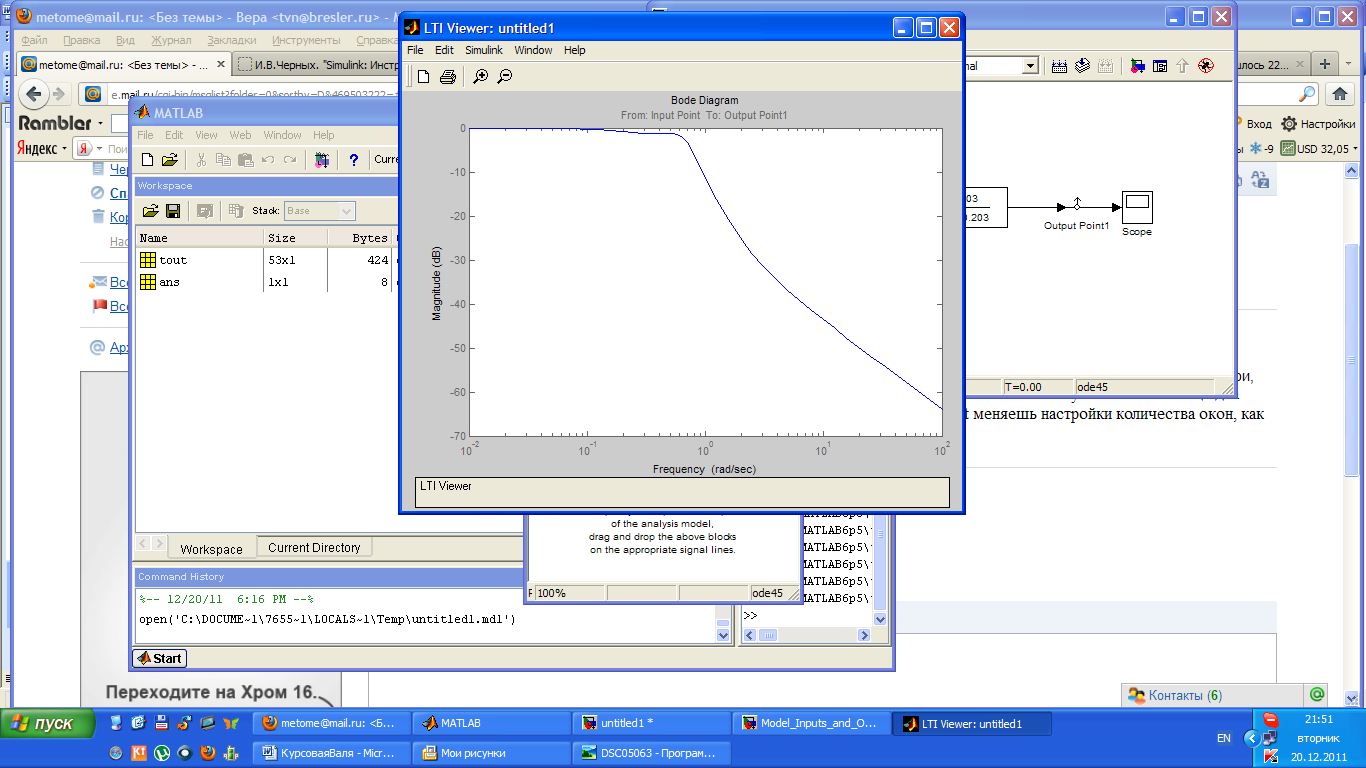
_{3.4 Приняв h=1, выберите k так, чтобы запас устойчивости по амплитуде был не менее 6 Дб, а запас по фазе – не менее 30º (используйте ЛАФЧХ разомкнутой системы без регулятора).}

_{ФЧХ пересекает линию φ=180˚ при амплитуде -5,54. Поднимем Опустим ЛАЧХ на 0,5 дБ.}

_{ЛАЧХ пересекает ось ординат при φ=212˚, т.е. запас по фазе обеспечен.}

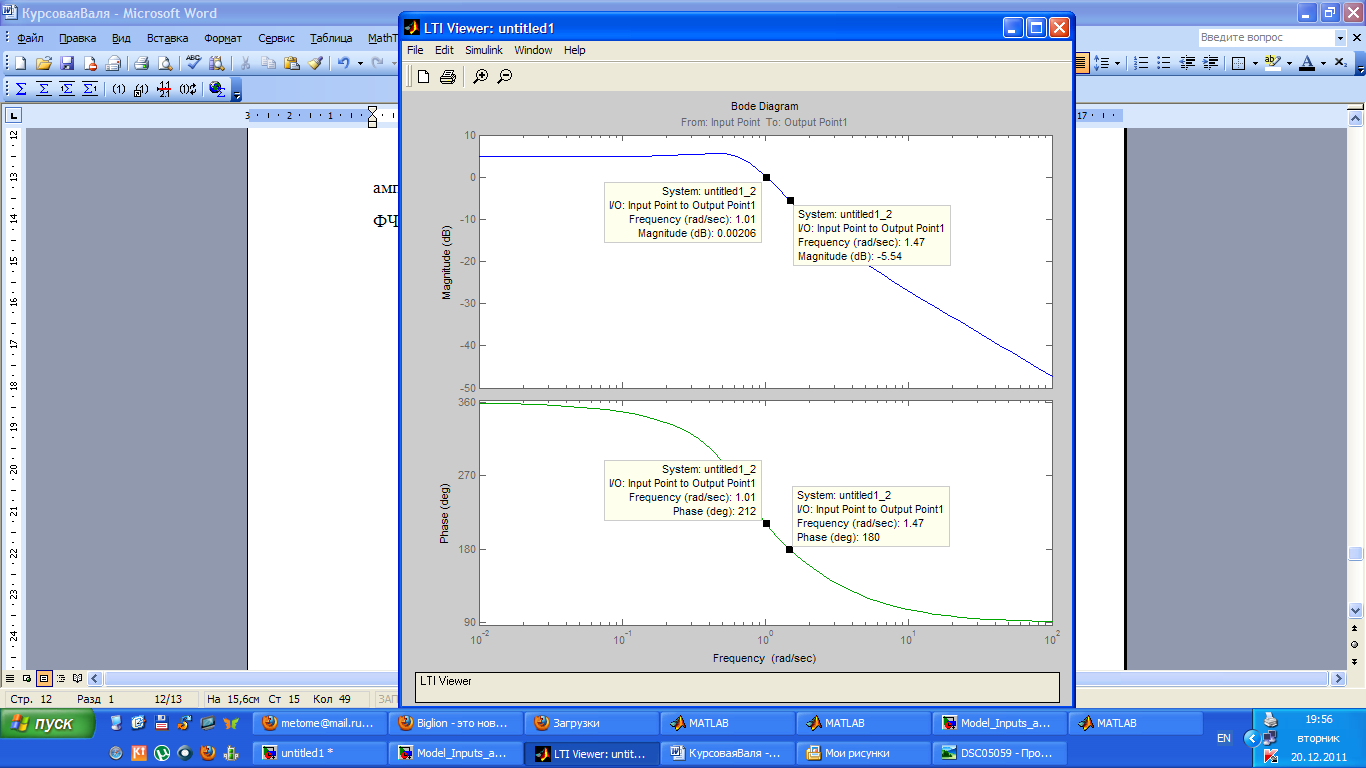
_{Найдем k.}

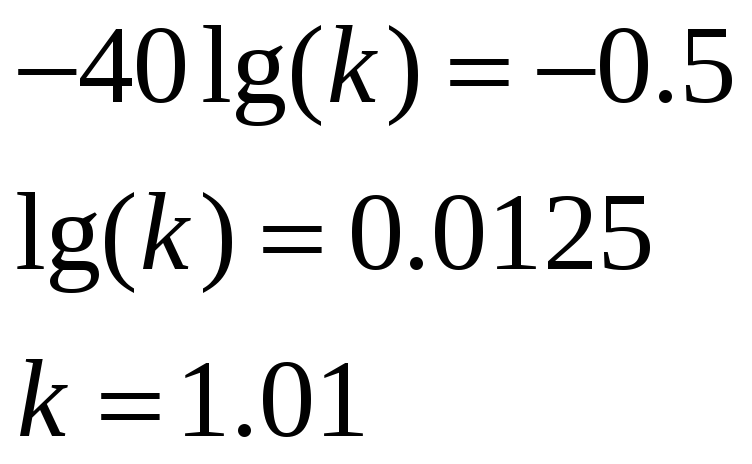
_{Коэффициент усиления практически равен единице.}

5. _{Постройте переходный процесс на выходе при выбранном значении k.}

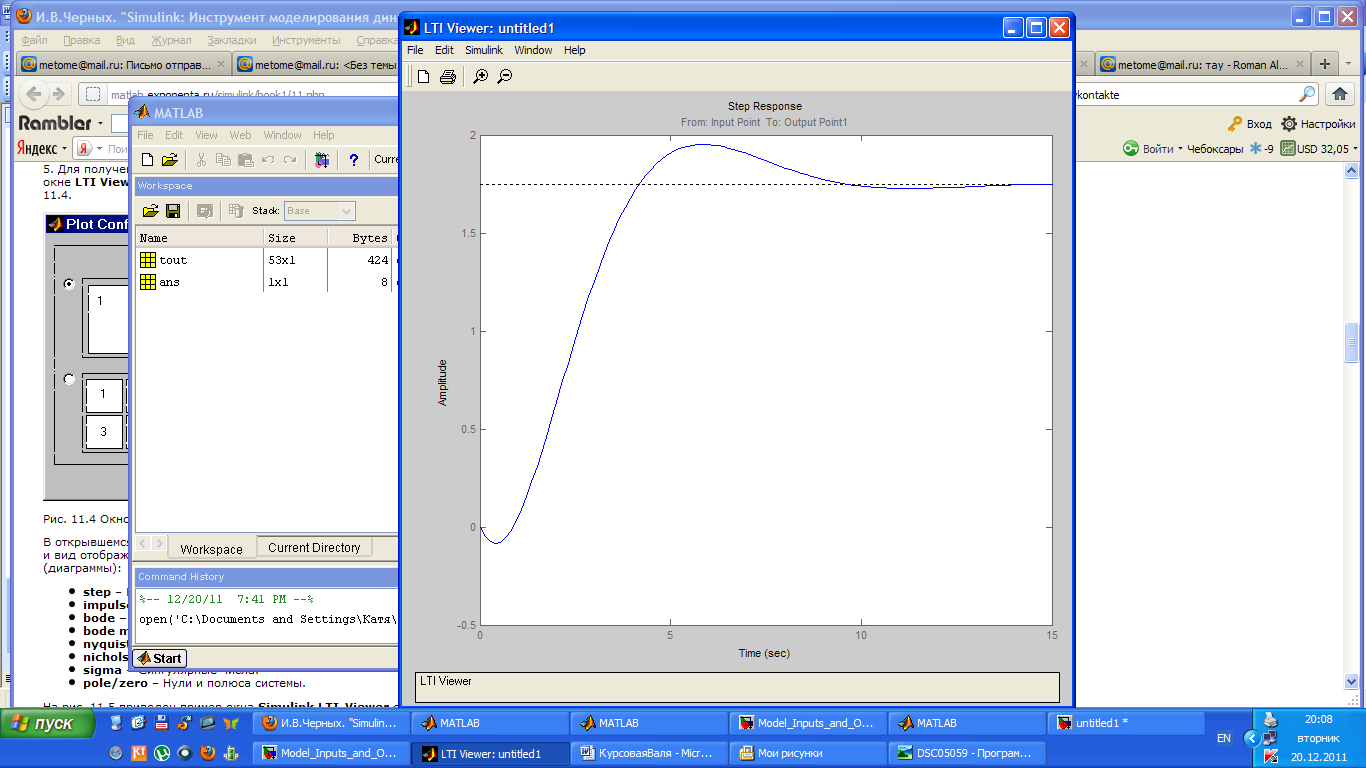
5. _{Оцените время переходного процесса и перерегулирование, покажите их на графике.}

_{Время переходного процесса – это время, после которого отклонение выхода системы от установленного значения не превышает 5%.}

_{Перерегулирование – это величина, которая показывает (в %) насколько максимум выходного сигнала во время переходного процесса больше установившегося значения.}

_{Установившееся значение равно 1,75}

_{Максимум выходного сигнала равен 1,95.}

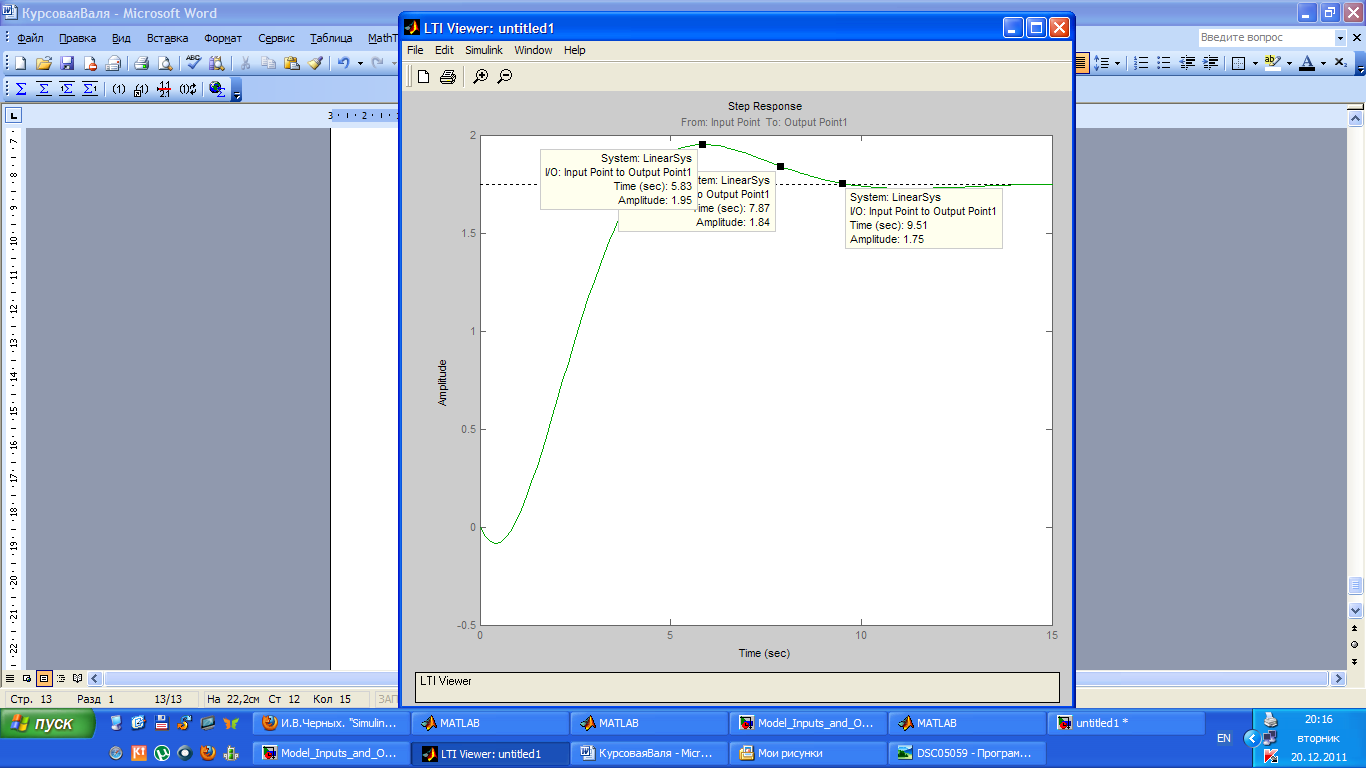
_{Тогда получим:}

_{tп = 7,87 – время переходного процесса.}

5. _{Является ли замкнутая система астатической? Почему?}

_{Системы называется астатической, если в установившемся режиме отсутствует статическая ошибка.}

_{Для того, чтобы система была астатической, нужно, чтобы передаточная функция по ошибке имела множитель p.}

_{Передаточная функция замкнутой системы для ошибки равна:}

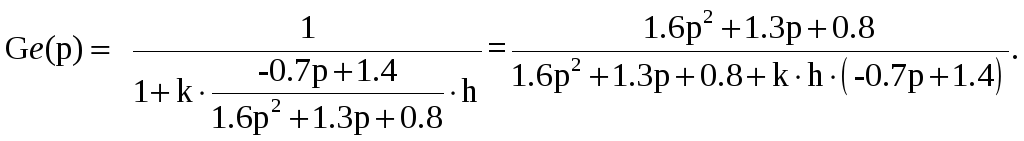
_{Отсюда:}

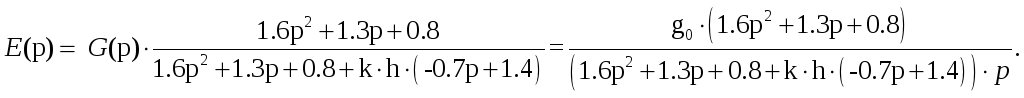_{Согласно теореме о конечном значении}

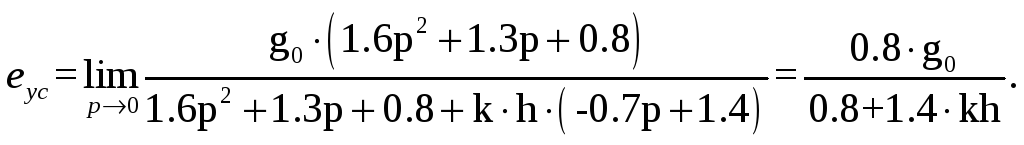
_{Т.е. мы имеем статическую ошибку и наша система не астатическая.}

5. _{Используйте пропорционально-интегральный регулятор (ПИ-регулятор) с передаточной фунуцией}

_{при α=1.}

_{С помощью критерия Гурвица определите, какие ограничения должны быть наложены на k, чтобы системы была устойчивой. Выберите коэффициент k, равный среднему арифметическому между минимальным и максимальным допустимыми значениями.}

_{Рассмотрим характеристическое уравнение.}

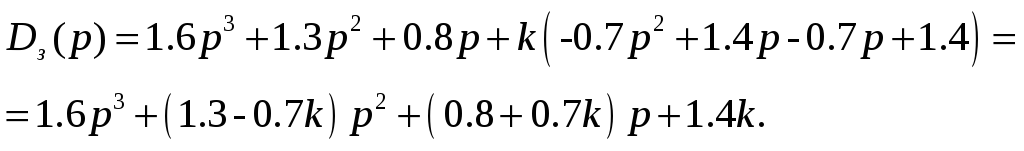
_{По критерию Гурвица:}

_{Получим:}

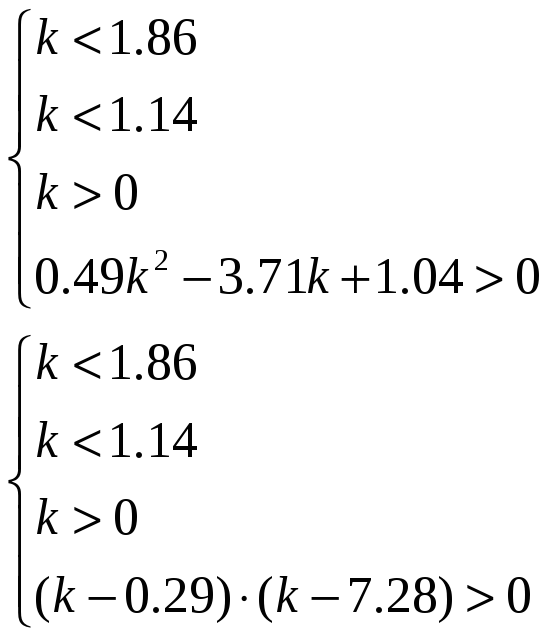
Получили, что

0<k<0.29.

Для дальнейших расчетов примем

_{3.9.Постройте переходный процесс на выходе при выбранном регуляторе. Оцените время переходного процесса и перерегулирование, покажите их на графике.}

_{Подставим полученное значение k в передаточную функцию.}

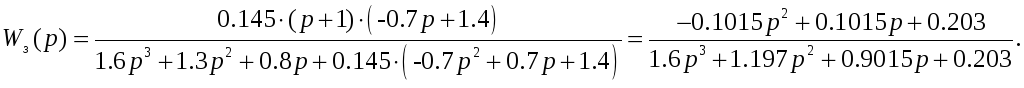
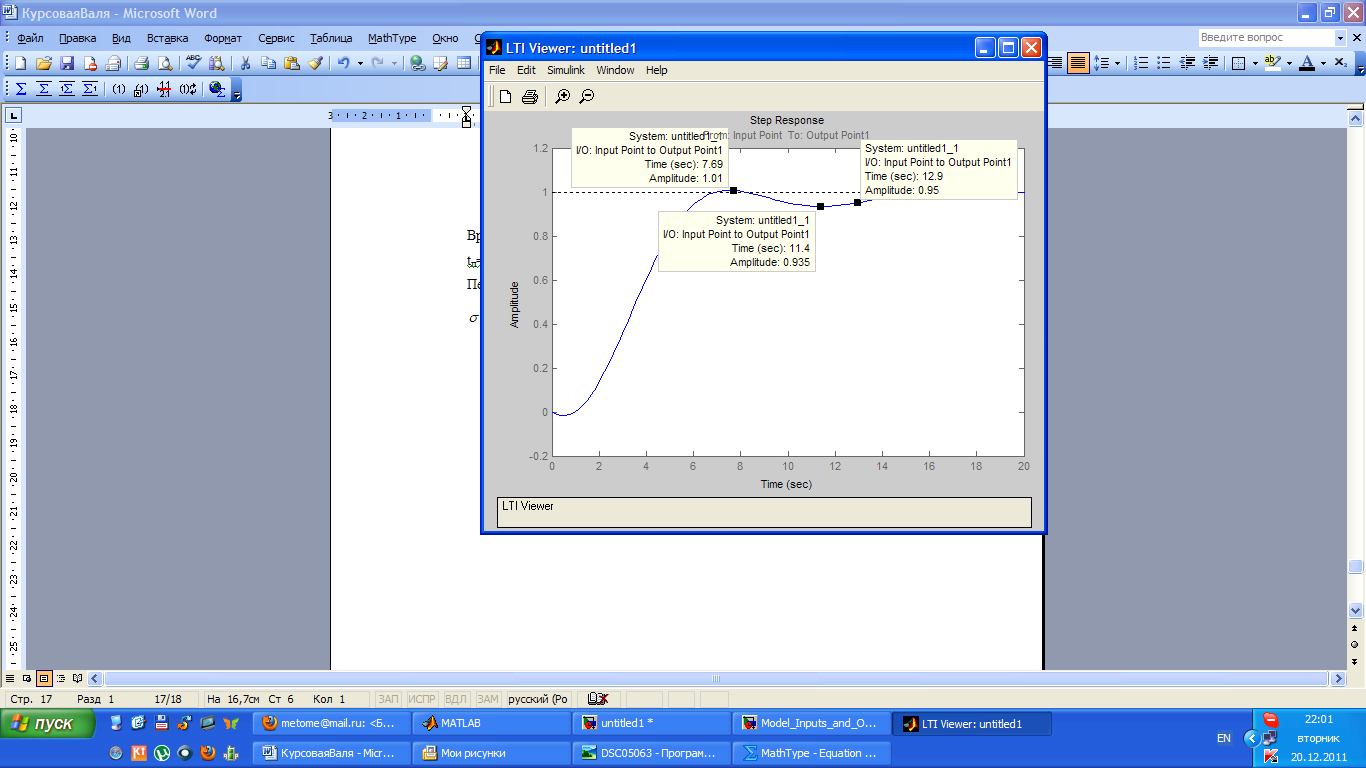
Время переходного процесса:

t_п=12,9 с

Перерегулирование:

5. Постройте амплитудную частотную характеристику полученной замкнутой системы и определите показатель колебательности М.

В нашем случае определить показатель колебательности невозможно, т.к. нет максимума характеристики.