Применение принципа Даламбера.

1.

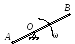Тонкий однородный стержень AB (AO=l₁, OB=l₂) массой m =1 кг вращается с постоянной угловой скоростью ω =5 с^-1 вокруг оси, перпендикулярной стержню. Определить модуль главного вектора сил инерции стержня, если размеры l₁ = 0,2 м, l₂ = 0,4 м.

2.

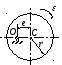
Определить главный момент сил инерции однородного диска радиуса r = 0,2 м массой m = 2 кг относительно оси вращения О, смещенной на расстояние e = 0,1 м от центра масс С. Диск вращается равноускоренно с угловым ускорением ε = 10 с^-2.

3.

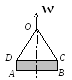
Строительную деталь массой m = 600 кг поднимают с ускорением w =1,5 м/c². Определить силу натяжения наклонных ветвей подъемных канатов.

4.

Два одинаковых тела с массой 1 кг каждый соединены между собой нитью и движутся по горизонтальной плоскости под действием силы F =40 Н. Коэффициент трения скольжения тел по плоскости f = 0,1. Определить натяжение нити.

5.

Два тела с одинаковыми массами m₁ = m₂ = 1 кг соединены стержнем и движутся по горизонтальной направляющей под действием сил F₁ = 3 кН и F₂ = 12 кН. Коэффициент трения скольжения тел по плоскости f = 0,2. Определить усилие в стержне.

6.

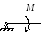Однородный стержень длиной l = 0,6 м начинает вращаться в горизонтальной плоскости из состояния покоя под действием пары сил с моментом М = 40 Нм. Определить модуль силы реакции шарнира в начальный момент движения.

7.

Три одинаковых груза массы m каждый связаны нерастяжимыми гибкими нитями по схеме, приведенной на рисунке. Пренебрегая трением, а также массой блока и нитей, определить усилие в нити, соединяющей первый и второй грузы.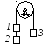

8.

Груз М₁ массой m₁ находится на шероховатой горизонтальной плоскости. К нему прикреплена нерастяжимая нить, перекинутая через идеальный блок А, на другом конце которой прикреплен груз М₂ массой m₂. Пренебрегая массой блока и нити, определить коэффициент трения f груза М₁ о плоскость, если грузы движутся с ускорением, равным по величине w.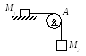

Применение принципа возможный перемещений.

1.

На клин 3 действует сила F = 100 Н. Определить с какой силой толкатель 2 прижимает деталь 1 к опорной плоскости в положении равновесия, если угол α =11⁰.

2.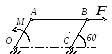

К шатуну АВ шарнирного параллелограмма ОАВС приложена горизонтальная сила F = 50 Н. Определить модуль момента М пары сил, которую необходимо приложить к кривошипу ОА длиной 10 см, для того, чтобы уравновесить механизм.

3.

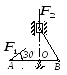
Определить модуль силы F₁, которую необходимо приложить к кривошипу АВ, для того, чтобы механизм находился в равновесии, если сила F₂ = 100 Н и расстояние ОА = 2 ОВ.

4.

Определить модуль момента М пары сил, который необходимо приложить к шкиву 3 для равномерного подъема груза 1 весом 900 Н. Радиусы шкивов см.

5.

К коромыслу О₁А четырехзвенного механизма приложен вращающий момент М₁. Определить момент М₂, передаваемый на коромысло О₂В, в положении механизма, изображенном на рисунке, если О₁А = 6 см, О₁О₂ = см, О₂В = см,