Применение теоремы об изменении кинетической энергии.

1.

Однородный стержень длиной l и массой m, который может вращаться вокруг горизонтальной оси А, отклонен от устойчивого положения равновесия на 90⁰ и отпущен без начальной скорости. Найти угловую скорость стержня в момент, когда он будет занимать вертикальное положение. Сопротивлением воздуха и трением пренебречь.

2. Однородный цилиндр, получив начальную скорость центра, равную v₀, катится без скольжения вверх по наклонной плоскости. Пренебрегая трением качения и сопротивлением воздуха, определить, на какую высоту поднимется центр цилиндра.

3.

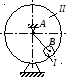Колесо І массой m₁ может катиться без скольжения в вертикальной плоскости внутри неподвижной шестерни ІІ и приводится в движение кривошипом АВ, длиной l и массой m. В начальный момент кривошип составлял угол α = 60⁰ с вертикалью и был отпущен без начальной скорости. Определить его угловую скорость в момент прохождения через равновесное положение. Кривошип считать однородным стержнем, колесо І – однородным диском. Трением пренебречь.

4. Точка приложения силы 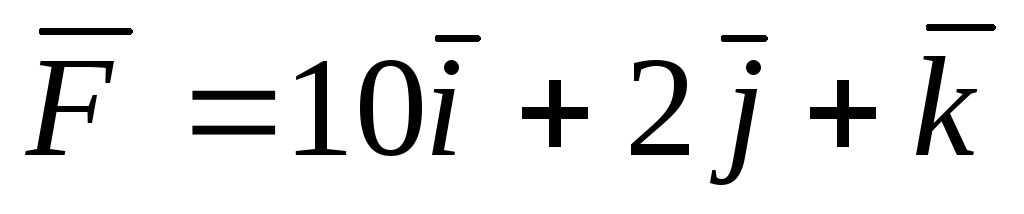(Н) движется согласно уравнениям

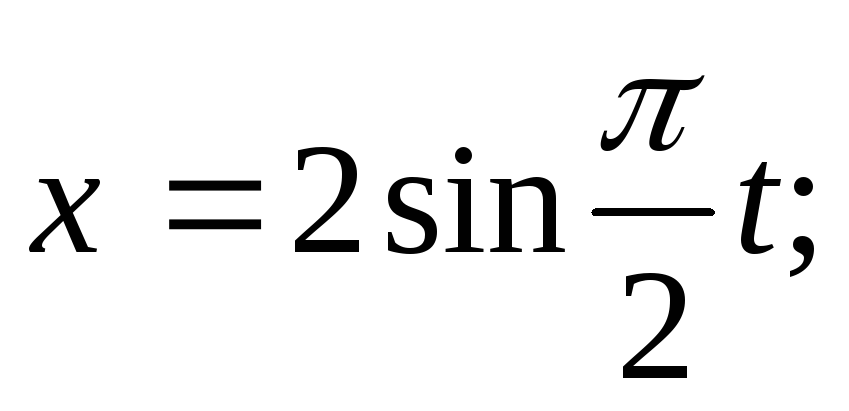
(x, y, z – в метрах; t – в секундах). Найти работу этой силы за время с.

с начала движения точки.

5.

В планетарном механизме кривошип ОА вращается с угловой скоростью ω₀. Радиусы колес . Определить кинетическую энергию колеса 3, если его масса равна

6.

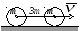Механическая система состоит из двух одинаковых колес массы m каждое и прямолинейного однородного стержня, соединяющего оси этих колес. Пренебрегая проскальзыванием колес по горизонтальной опорной плоскости и считая их однородными сплошными дисками, найти кинетическую энергию всей системы, если масса соединительного стержня равна 3m, а скорость центра одного из колес равна v.

7.

Определить кинетическую энергию механизма, состоящего из кривошипа ОА массы 3m и длины l, шатуна АВ массы m и шарнирно связанного с ним колеса массы m, катящегося без скольжения по горизонтальной плоскости. Кривошип ОА вращается с угловой скоростью ω и в рассматриваемый момент времени вертикален. Кривошип и шатун считать однородными тонкими стержнями; масса колеса равномерно распределена по его ободу.

8.

Найти кинетическую энергию эллипсографа, если ОА=АВ=АС=

=l, угловая скорость кривошипа ОА равна ω, масса звеньев составляет Кривошип ОА и линейку ВС считать тонкими однородными стержнями. Угол φ принять равным 45⁰.

9.

Однородное тонкое кольцо массы m и радиуса R катится без скольжения по горизонтальной плоскости, при этом центр С кольца имеет постоянную скорость . C кольцом с помощью шарнира В связан стержень АВ такой же массы m и длины l>2R. Конец А стержня перемещается по той же плоскости, что и кольцо. Определить кинетическую энергию механической системы, в положении, показанном на рисунке, когда шарнир В совпадает с наивысшей точкой кольца.

10.

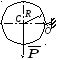
Однородный круглый диск веса P и радиуса R может вращаться вокруг горизонтальной оси О в вертикальной плоскости. В начальный момент радиус ОС горизонтален и диск отпущен без начальной скорости. Пренебрегая трением, определить угловую скорость ω диска в момент, когда диск повернется на угол 30⁰.

11.

Однородный прямолинейный стержень ОА длины l, закрепленный в вертикальной плоскости с помощью шарнира О и нити АВ, составляет угол α = 30⁰ с горизонтом. Пренебрегая сопротивлениями, найти наибольшую угловую скорость стержня при обрыве нити АВ.

12.

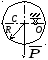Однородное тонкое кольцо веса P и радиуса R может вращаться вокруг горизонтальной оси О в вертикальной плоскости. В начальный момент времени линия ОС () горизонтальна и кольцо отпущен без начальной скорости. Пренебрегая трением, определить угловую скорость ω кольца в момент, когда оно повернется на угол 90⁰.

13.

Однородное тонкое кольцо радиуса R скатывается без скольжения по наклонной плоскости из состояния покоя. Центр кольца, пройдя расстояние , приобрел скорость v. Определить коэффициент трения качения f_k кольца о плоскость, если угол наклона плоскости к горизонту равен α.

14.

Ременная передача начинает движение из состояния покоя под действием постоянного момента пары сил М = 2,5 Нм. Моменты инерции шкивов относительно их осей вращения I₂ = 2I₁ = 1 кг м². Определить угловую скорость шкива 1 после трех оборотов, если радиусы шкивов R₂ = 2R₁ .

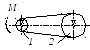
15.

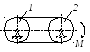Движение шкива 2 ременной передачи начинается из состояния покоя под действием постоянного момента М = 0,5 Нм.

После трех оборотов одинаковые по массе и размерам шкивы 1 и 2 имеют угловую скорость 2 с^-1. Определить момент инерции одного шкива относительно оси вращения.