Варіант 2
1. Довести збіжність ряду й знайти його суму:
.
2. Дослідити на збіжність ряди з додатними членами:
а)
;
б)
;
в)
;
г)
.
3. Дослідити на умовну й абсолютну збіжність ряди зі знакопочережними членами:
а)
;
б)
.
4. Використовуючи необхідну
ознаку збіжності ряду, довести
справедливість рівності:
.
5. Знайти область збіжності для таких функціональних рядів:
а)
;
б)
;
в)
.
6. Розкласти в ряд Маклорена або Тейлора функцію f(x) в околі точки х0. Указати область збіжності отриманого ряду до цієї функції:
.
7. Використовуючи розкладання
підінтегральної функції в степеневий
ряд, обчислити зазначений визначений
інтеграл з точністю до 0,001:
.
8. Використовуючи теореми про почленне інтегрування й диференціювання степеневих рядів, знайти суми рядів:
а)
;
б)
.
9. Розкласти в ряд Фур'є
східчасту періодичну функцію f(x), зробити
креслення:
10. Розкласти в ряд Фур'є
функцію f(x), задану на інтервалі (0; π),
довизначивши її парним або непарним
способом. Побудувати графік суми
отриманого ряду:
.
11. Скориставшись розкладанням функції f(x) у ряд Фур'є в зазначеному інтервалі, знайти суму числового ряду
.
Варіант 3
1. Довести збіжність ряду й знайти його суму:
.
2. Дослідити на збіжність ряди з додатними членами:
а)
;
б)
;
в)
;
г)
.
3. Дослідити на умовну й абсолютну збіжність ряди зі знакопочережними членами:
а)
;
б)
.
4. Використовуючи необхідну
ознаку збіжності ряду, довести
справедливість рівності
.
5. Знайти область збіжності для таких функціональних рядів:
а)
;
б)
;
в)
.
6. Розкласти в ряд Маклорена або Тейлора функцію f(x) в околі точки х0. Указати область збіжності отриманого ряду до цієї функції:
.
7. Використовуючи розкладання
підінтегральної функції в степеневий
ряд, обчислити зазначений визначений
інтеграл з точністю до 0,001:
.
8. Використовуючи теореми про почленне інтегрування й диференціювання степеневих рядів, знайти суми рядів:
а)
;
б)
.
9. Розкласти в ряд Фур'є
східчасту періодичну функцію f(x),
зробити креслення:
10. Розкласти в ряд Фур'є функцію f(x), задану на інтервалі (0; π), довизначивши її парним або непарним способом. Побудувати графік суми отриманого ряду:
.
11. Скориставшись розкладанням функції f(x) у ряд Фур'є в зазначеному інтервалі, знайти суму числового ряду
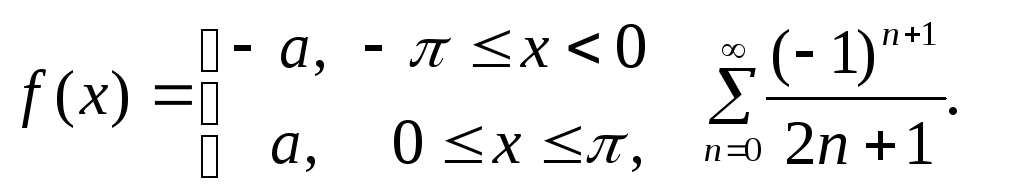
Варіант 4
1. Довести збіжність ряду й знайти його суму:
.
2 . Дослідити на збіжність ряди з додатними членами:
а)
;
б)
;
в)
;
г)
.
3. Дослідити на умовну й абсолютну збіжність ряди зі знакопочережними членами:
а)
;
б)
.
4. Використовуючи необхідну
ознаку збіжності ряду, довести
справедливість рівності
.
5. Знайти область збіжності для таких функціональних рядів:
а)
;
б)
;
в)
.
6. Розкласти в ряд Маклорена або Тейлора функцію f(x) в околі точки х0. Указати область збіжності отриманого ряду до цієї функції:
.
7. Використовуючи розкладання
підінтегральної функції в степеневий
ряд, обчислити зазначений визначений
інтеграл з точністю до 0,001:
.
8. Використовуючи теореми про почленне інтегрування й диференціювання степеневих рядів, знайти суми рядів:
а)
;
б)
.
9. Розкласти в ряд Фур'є
східчасту періодичну функцію f(x),
зробити креслення:
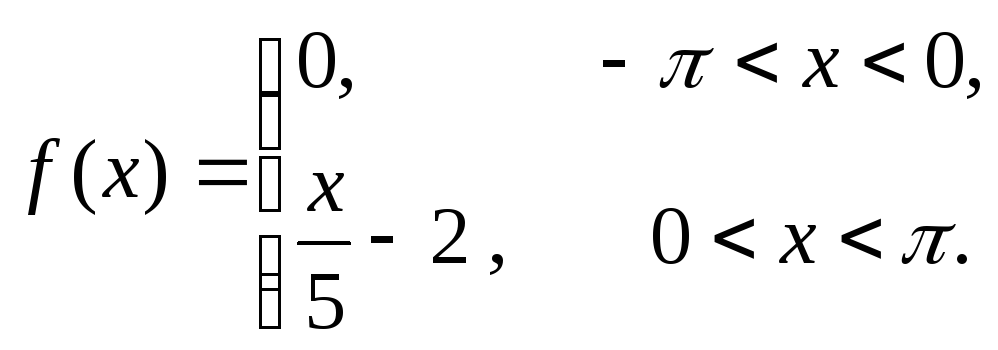
10. Розкласти в ряд Фур'є функцію f(x), задану на інтервалі (0; π), довизначивши її парним або непарним способом. Побудувати графік суми отриманого ряду:
.
11 Скориставшись розкладанням функції f(x) у ряд Фур'є в зазначеному інтервалі, знайти суму числового ряду
.