6. Розкласти в ряд Маклорена або Тейлора функцію f(X) в околі точки х0. Вказати область збіжності отриманого ряду до цієї функції:

.

За допомогою методу невизначених коефіцієнтів подамо дріб у вигляді суми найпростіших:

,

тоді

, тотожна рівність справедлива при будь-яких значеннях х.

.

Нескінченно спадна геометрична прогресія

при .

Таким чином,

область збіжності

область збіжності

Тоді

Область збіжності отриманого ряду визначимо із системи

, остаточно

7. Використовуючи розкладання підінтегральної функції в степеневий ряд, обчислити визначений інтеграл з точністю до 0,001:

.

Оскільки при всіх, то

область збіжності

Степеневий ряд в області збіжності можна почленно інтегрувати

Оскільки одержали знакопочережний ряд, що задовольняє всі умови ознаки Лейбніца, то за зауваженням до ознаки Лейбніца, модуль залишку такого ряду менше модуля першого відкинутого члена.

, де

.

Тобто при заміні суми ряду (S) частковою сумою (S_n) відкидаються всі доданки, які менше заданої точності (ε).

з точністю ε = 0,001.

8. Використовуючи теореми про почленне інтегрування й диференціювання степеневих рядів, знайти суми рядів:

а) ; б).

У прикладі пункту а зробимо заміну змінних sin x = y, одержимо ряд .

Визначимо область збіжності ряду (1) ; (2);

;

.

За ознакою Даламбера ряд (2) збігається, якщо . Дослідимо ряд (1) на кінцях області збіжності. Нехайу=-1, ряд (1) набере вигляду

(3)– знакосталий ряд, за граничною формою ознаки порівняння (порівнюємо з рядом) цей ряд збігається.

Нехай у = 1, підставимо в ряд (1):

, оскільки ряд (3) збігається, то останній ряд збігається, причому абсолютно (див. теорему про абсолютну збіжність).

Таким чином, ряд (1) збігається при всіх до суми.

Цей ряд можна почленно диференціювати усередині області збіжності:

;

як нескінченно спадна геометрична прогресія, де b₁ = y, q= – y.

Почленно інтегруємо останню рівність:

;

Ще раз почленно інтегруємо:

.

Отже , а

.Остаточно

.

Оскільки , то остання рівність справедлива при всіх

Розглянемо приклад пункту б:

Всі ці ряди збігаються при , це легко довести за ознакою Даламбера.

Визначимо суму ряду (сума нескінченно спадної геометричної прогресії).

, для визначення суми цього ряду використовуємо теорему про почленне інтегрування степеневих рядів в області збіжності.

Тоді .

.

.

.

Щоб визначити суму , двічі продиференціюємо:

9. Розкласти в ряд Фур'є східчасту періодичну функцію f(X), зробити креслення:

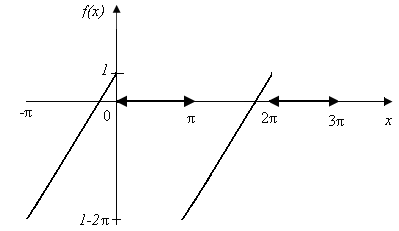
Період , функція загального вигляду.

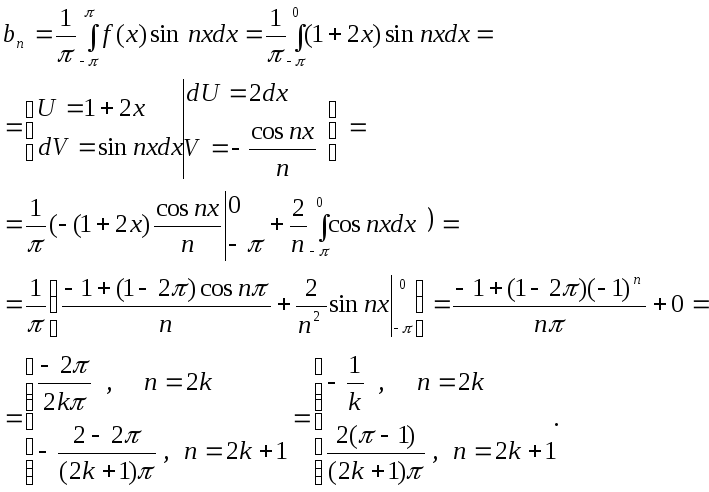
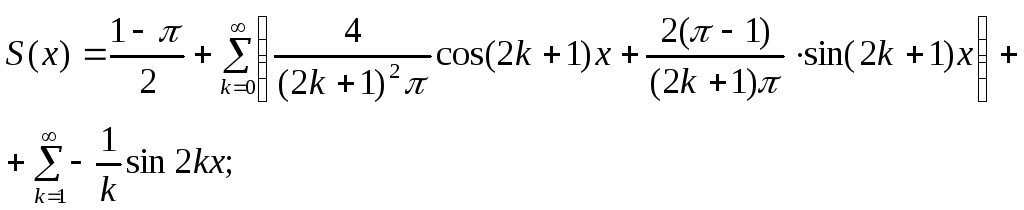
10. Розкласти в ряд Фур'є функцію f(x), задану на інтервалі (0; π), довизначивши її парним або непарним чином. Побудувати графік суми отриманого ряду:

(непарна).

Використовуючи теорему Діріхле, побудуємо графік суми ряду:

Період , оскільки функція непарна, то.

або

11. Скориставшись розкладанням функції f(x) у ряд Фур'є в зазначеному інтервалі, знайти суму даного числового ряду:

.

, функція загального вигляду.

.

.

Підберемо х таке значення, щоб . При

, тоді й

За теоремою Діріхле в точках неперервності функції , а в точках розриву.

При , тоді

Умови обов'язкового домашнього завдання 3

ВАРІАНТ 1

1.Довести збіжність ряду й знайти його суму:

.

2. Дослідити на збіжність ряди з додатними членами:

а) ; б);

в) ; г)

3. Дослідити на умовну й абсолютну збіжність ряди зі знакопочережними членами:

а) ; б)

4. Використовуючи необхідну ознаку збіжності ряду, довести справедливість рівності:

5. Знайти область збіжності для таких функціональних рядів:

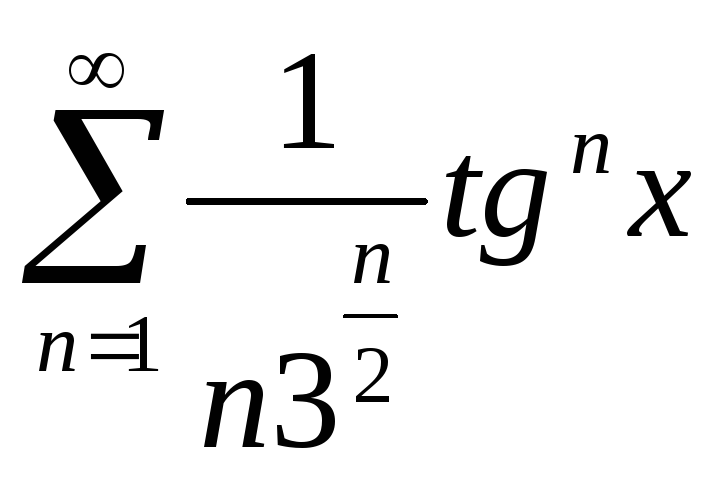а) ; б); в).

6. Розкласти в ряд Маклорена або Тейлора функцію f(x) в околі точки х₀. Указати область збіжності отриманого ряду до цієї функції: .

7. Використовуючи розкладання підінтегральної функції в степеневий ряд, обчислити зазначений визначений інтеграл з точністю до 0,001:

8. Використовуючи теореми про почленне інтегрування й диференціювання степеневих рядів, знайти суми рядів:

а) ; б).

9. Розкласти в ряд Фур'є східчасту періодичну функцію f(x), зробити креслення:

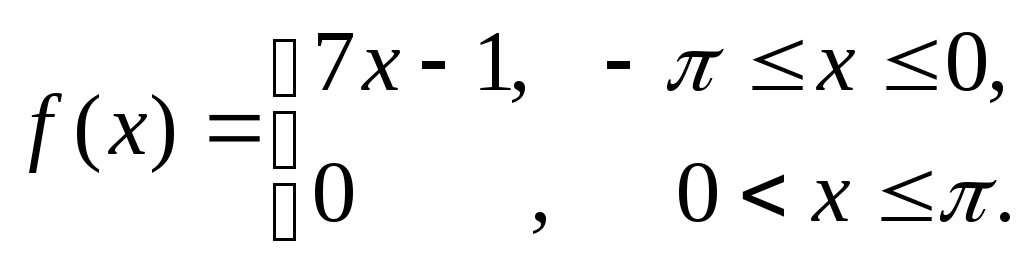
10. Розкласти в ряд Фур'є функцію f(x), задану на інтервалі (0; π), довизначивши її парним або непарним способом. Побудувати графік суми отриманого ряду: .

11. Скориставшись розкладанням функції f(x) у ряд Фур'є в зазначеному інтервалі, знайти суму числового ряду

.