Геометрия

1. Пространство 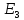. Скалярное, векторное и смешанное произведение векторов. Приложения к решению задач.

Скалярное произведение векторов: определение, вычислительная формула. Свойства.

Векторное произведение векторов: определение, вычислительная формула, свойства.

Смешанное произведение векторов: определение, вычислительная формула, свойства.

Условия коллинеарности и компланарности векторов через произведения векторов.

Площадь треугольника, объем тетраэдра. Векторный метод решения задач школьного курса геометрии.

(1) §8, 9, 53, 55, 56, 58; (3) раздел 1, §9; раздел 2, §4, 5; (5) §6, 7, 8, 43-46.

2. Взаимное расположение двух плоскостей, прямой и плоскости, двух прямых в пространстве (в аналитическом отношении).

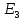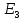Общее уравнение плоскости в . Плоскость – алгебраическая поверхность первого порядка. Исследование взаимного расположения двух плоскостей по их уравнениям. Задание и вывод уравнения прямой в . Исследование взаимного расположения прямой и плоскости по их уравнениям. Исследование взаимного расположения двух прямых в пространстве по их уравнениям. Примеры решения задач по изложенной теории.

(1) §57, 59-61, 63, 64; (3) раздел 2 §7-9, 11-13; (5) §48, 52, 54.

3. Группа движений (перемещений) плоскости. Классификация движений. Приложения движений к решению задач.

Определение преобразования движения. Движение первого и второго рода. Формулы движений плоскости. Свойства движений. Движения плоскости частного вида (параллельный перенос, осевая симметрия, поворот, скользящая симметрия): определения, формулы, свойства. Группа движений, подгруппы движений. Теоремы о классификации движений. Сведение движений к осевым симметриям. Задача на приложение движений.

(1) §39-44, 51; (3) раздел 1, §24-29, 35; (5) §28-31, 33.

4. Определение преобразования подобия плоскости. Группа преобразования подобия и ее подгруппы. Приложения преобразований подобия к решению задач.

Определение преобразования подобия. Частные виды подобия: гомотетия, движение. Гомотетия: определение, формулы, свойства. Теорема о представлении подобия в виде произведения гомотетии и движения. Аналитическое выражение преобразований подобия. Группа подобий и ее подгруппы. Задача на применение подобия.

(1) §39, 40, 46, 47, 51; (3) раздел 1 §24, 25, 31, 32, 35; (5) §28-31, 33.

5. Группа аффинных преобразований плоскости и ее подгруппы. Приложение аффинных преобразований к решению задач.

Определение аффинной системы координат на плоскости. Определение аффинного преобразования плоскости, задание аффинного преобразования, его формулы. Свойства аффинных преобразований. Группа аффинных преобразований и ее подгруппы. Задача на применение аффинных преобразований.

(1) §48, 50, 51; (3) раздел 1 §24, 25, 34, 35.

6. Проективная плоскость и ее модели. Группа проективных преобразований. Приложения к решению задач.

Перспективное соответствие между плоскостью и связкой. Определение расширенных прямой, плоскости, пространства. Модели проективной плоскости. Принципы двойственности. Теоремы Дезарга. Определение проективного преобразования проективной плоскости. Группа проективных преобразований. Приложение проективных теорем к решению задач на построение одной линейкой.

(2) §1, 4, 7, 8, 11, 13, 25; (4) раздел 3 §1, 4, 7-9, 14, 22; (6) §1-4, 11, 14, 16, 27.

7. Изображения плоских и пространственных фигур в параллельной проекции. Позиционные и метрические задачи.

Параллельные проектирование. Свойства параллельного проектирования. Изображение плоских фигур в параллельной проекции (треугольник, четырехугольник, правильный прямоугольник, круг). Изображение правильных треугольника и четырехугольника, вписанных в окружность. Изображения пространственных фигур (призма, пирамида, цилиндр, конус, шар) в параллельной проекции. Полные и неполные изображения фигур. Пример решения позиционной или метрической задачи на плоском изображении.

(2) §26-33; (4) раздел 3 §28-29, 31-34; (6) §38, 40,41.