Добавил:

Loll384 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Технический Университет

Предмет:

Математика

Файл:

nikolaeva_lineinaya_algebra_konspekt_lekciy_chast1

.pdf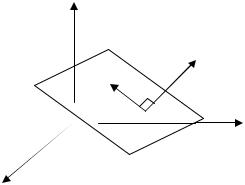

Скачиваний:

Добавлен:

05.09.2020

Размер:

842.16 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>

Z					Пусть M ( x, y, z ) – произвольная точка на
				n	плоскости	α .
		M		n	Тогда AM	= ( x − x0 , y − y0 , z − z0 )	и
					Тогда AM	= ( x − x0 , y − y0 , z − z0 )	и
					( AM , n) = 0 (рис. 45).
α			A		( AM , n) = 0 (рис. 45).
					Y Вычислив скалярное произведение, по-

	О
					лучим:
X					A( x − x0 ) + B ( y − y0 ) + C ( z − z0 )		(3.38)
		Рис. 45			A( x − x0 ) + B ( y − y0 ) + C ( z − z0 )		(3.38)
		Рис. 45

Координаты точек, лежащих в плоскости α , связаны соотношением (3.38). Если же M α , то AM не перпендикулярен n ( AM , n) ¹ 0 , значит, координа-

ты такой точки не удовлетворяют полученному уравнению. Поэтому (3.38) – уравнение плоскости, проходящей через заданную точку перпендикулярно за-

данному вектору. Заметим, что это уравнение линейно относительно	x, y, z.
Раскрыв скобки в (3.38), получим Ax + By + Cz − Ax0 − By0 − Cz0 = 0 .
Обозначим D = − Ax0 − By0 − Cz0 , тогда уравнение (3.38) примет вид:
Ax + By + Cz + D = 0.	(3.39)

(3.39) – общее уравнение плоскости в пространстве, n = ( A, B,C ) – ее нормаль.

ОПРЕДЕЛЕНИЕ. Любой ненулевой вектор n , перпендикулярный плос-

кости α , называется ее нормальным вектором, или нормалью.

ОСОБЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОСТИ

Выясним, какие особенности в расположении плоскости влечет за собой равенство нулю одного или нескольких коэффициентов в уравнении (3.39).

1)Ax + By + Cz = 0 координаты точки O (0,0,0) удовлетворяют уравнению, значит, плоскость проходит через начало координат.

2)By + Cz + D = 0 n = (0, B,C ) ^ i = (1,0,0), так как (n,i ) = 0 . Но n ^ α ,

значит, плоскость α OX .

3)Ax + Cz + D = 0 n = ( A,0,C ) ^ j = (0,1,0) , так как (n, j ) = 0 . Значит,

плоскость α OY .

4)Ax + By + D = 0 n = ( A, B,0) k = (0,0,1) , так как (n, k ) = 0 . Значит, плоскость α OZ .

5)By + Cz = 0 α OX , O (0,0,0) α α проходит через OX .

6)Ax + Cz = 0 α OY , O (0,0,0) α α проходит через OY .

7)Ax + By = 0 α OZ , O (0,0,0) α α проходит через OZ .

n = (0,0,C ) i		R
8) Cz + D = 0 R	R n OZ α OZ или α XOY .

n = (0,0,C ) j

n = (0, B,0) i		R
9) By + D = 0 R	R n OY α OY или α XOZ .
n = (0, B,0) k

n = ( A,0,0) k		R
10) Ax + D = 0 R	R n OX α OX или α YOZ .
n = ( A,0,0) j

11)Ax = 0 x = 0 – плоскость YOZ .

12)By = 0 y = 0 – плоскость XOZ .

13)Cz = 0 z = 0 – плоскость XOY .

УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ

Пусть плоскость α не параллельна ни одной из координатных осей и не проходит через начало координат. Тогда она отсекает на координатных осях отрезки a, b, c (рис. 46). Выведем уравнение такой плоскости.

			Рассмотрим Ax + By + Cz + D = 0 –
Z			общее уравнение плоскости.
C c			Так как A(a,0,0) α , то
			Aa + D = 0 A = −			D	.
			Aa + D = 0 A = −				.
О	B	Y				a
О	B	Y	Аналогично B (0,b,0) α
A	b		Аналогично B (0,b,0) α
A	b
a				D
X			Bb + D = 0 B = −	D	; C (0,0,c) α
X	Рис. 46		Bb + D = 0 B = −		; C (0,0,c) α
	Рис. 46			b

Cc + D = 0 C = - D .

Подставив А, В, С в общее уравнение, получим

x -

y -

z + D = 0, D ¹ 0

(3.40)

b c

(3.40) – уравнение плоскости в отрезках.

ПРИМЕР. Вычислить объем тетраэдра, образованного плоскостями

2x − 3y − 4z + 12 = 0, x = 0, y = 0, z = 0.

Перепишем уравнение плоскости в ви-

де (3.40):

-6

2x - 3y - 4z = -12 -

=1 –

уравнение данной плоскости в отрез-

ках. Поэтому (рис. 47)

a = 6, b = 4, c = 3 V =

× 6 × 4 ×3 =12 .

Рис. 47

УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТРИ ТОЧКИ

Пусть в некоторой пдск заданы три точки, не лежащие на одной прямой: A( x1, y1, z1 ), B ( x2 , y2 , z2 ), C ( x3 , y3 , z3 ) . Известно, что через них проходит единственная плоскость α .

Чтобы вывести ее уравнение, рассмотрим произвольную точку этой плоскости

M ( x, y, z ). Тогда AM , AB, AC –		компланарные векторы, и их смешанное про-
изведение равно нулю: ( AM , AB, AC ) = 0 . Тогда по формуле (2.9) получим
	x - x1	y - y1	z - z1
	x - x1	y - y1	z - z1
	x2 - x1	y2 - y1	z2 - z1	= 0	(3.41)
	x3 - x1	y3 - y1	z3 - z1

(3.41) – уравнение плоскости, проходящей через три точки.

ЗАМЕЧАНИЕ. Если точки лежат на одной прямой, то векторы AB и AC коллинеарны и их соответствующие координаты пропорциональны. Поэтому в определителе (3.41) две строки пропорциональны и по свойству 6 определителей он тождественно равен нулю, что означает, что координаты любой точки M ( x, y, z ) удовлетворяют уравнению (3.41). Это иллюстрация того факта, что

через прямую и любую точку можно провести плоскость.

ПРИМЕР. Написать уравнение плоскости, проходящей через точки

A(1,2, −3), B (0,1, −1), C (7, −3,5) .

x −1	y − 2	z + 3	= 0 2( x −1) + 20( y − 2) + 11( z + 3) = 0 2x + 20 y +11z − 9 = 0 .
x −1	y − 2	z + 3
−1	−1	2
6	−5	8

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

ОПРЕДЕЛЕНИЕ. Углом между плоскостями называется любой из двух смежных двугранных углов, образованных плоскостями при их пересечении. Если плоскости параллельны, то угол между ними равен 0 или π радиан.

Рассмотрим плоскости α1 : A1x + B1 y + C1z + D1 = 0, n1 = ( A1, B1,C1 ) и

α2 : A2 x + B2 y + C2 z + D2 = 0, n2 = ( A2 , B2 ,C2 ).

(

2 )

UR UUR

n , n

,α2 ) = (n1, n2 ) cosϕ =

Очевидно,

ϕ = (α1

UUR

или

cosϕ =

A1 A2 + B1B2 + C1C2

A 2

+ B

+ C 2

A 2

+ B

2 + C 2

Если α1 α2 , то

n1 n2

(n1, n2 ) = 0

–

условие перпендикулярности плоско-

стей.

Если α α

UUR

, то n n

–

условие параллельности плоскостей.

ПРИМЕР. Найти угол между плоскостями

α1 : 2x + 4 y + 5 = 0, и α2 : 2x − y + 2z = 0 .

UR	UUR		4	− 4
n	= (2, 4,0), n	= (2, −1, 2) cosϕ =	4	− 4	= 0 плоскости перпендикулярны.
n	= (2, 4,0), n	= (2, −1, 2) cosϕ =			= 0 плоскости перпендикулярны.
1	2		3	20
			3	20

ПРЯМАЯ ЛИНИЯ В ПРОСТРАНСТВЕ

Всякая линия в пространстве есть результат пересечения двух поверхностей. В частности прямую линию можно рассматривать как результат пересе-

чения двух плоскостей

α1 : A1x + B1 y + C1z + D1 = 0, n1 = ( A1, B1,C1 )

α2 : A2 x + B2 y + C2 z + D2 = 0, n2 = ( A2 , B2 ,C2 ).

Если α1 не параллельна α2 , то есть n1 не коллинеарен уравнений

A1x + B1 y + C1z + D1 = 0A2 x + B2 y + C2 z + D2 = 0

определяет прямую линию в пространстве.

n2 , то система

(3.42)

Уравнения (3.42) называются общими уравнениями прямой в пространстве.

		Очевидно, одна и та же прямая может быть
		результатом пересечения разных пар плоско-
		стей (рис. 48), поэтому прямую в пространст-
		стей (рис. 48), поэтому прямую в пространст-
		ве можно задать различными способами.
	L	Уравнения (3.42) неудобны в использовании,
	L	так как не дают представления о расположе-
Рис. 48		нии прямой относительно выбранной систе-
Рис. 48		мы координат.
		мы координат.

Поэтому выведем более удобные уравнения, эквивалентные (3.42), то есть из бесконечного множества плоскостей, проходящих через данную прямую, выберем в некотором смысле более заметную пару.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ

Пусть

в некоторой

пдск

задана

прямая L ,

проходящая

через точку

A( x0 , y0 , z0 ) параллельно ненулевому вектору

s = (m, n, p) . Такой вектор на-

зывается направляющим вектором этой прямой.

M ( x, y, z ) L

Для произвольной точки

вектор

AM s AM = t s, где t – не-

который числовой множитель. Кроме

того,

AM = r

− r0 , r –

радиус-вектор

точки M , r0 –

радиус-вектор точки A

Рис. 49

(рис. 49).

r = r0 + t s

Отсюда

(3.43)

(3.43) –

векторное уравнение прямой в пространстве. Из (3.43) получаем:

x = x0 + mt

+ nt

(3.44)

y = y0

+ pt

z = z0

(3.44) –

параметрические уравнения прямой в пространстве, t R –

параметр.

Выразим из каждого уравнения (3.44) параметр:

t =

x − x0

y − y0

z − z0

Тогда

x − x0

y − y0

z − z0

(3.45)

(3.45) –

канонические уравнения прямой в пространстве, то есть уравнения пря-

мой, проходящей через точку A( x0 , y0 , z0 ) параллельно вектору s = (m, n, p) .

Заметим, что уравнения (3.45) задают прямую						как результат пересечения плос-
костей
x − x		=	y − y		0
	0				0
	m		n
	m		n
x − x			z − z	0		,
	0	=		0
		=
	m		p

одна из которых параллельна OZ , а вторая – OY или как

x − x			=		y − y
	0					0
	m				n
	m				n
y − y		0			z − z	0
		0		=		0	,
	n			=	p		,
	n				p

где первая плоскость параллельна OZ , а вторая – OX .

Если прямая L проходит через две заданные точки B ( x1, y1, z1 ) и C ( x2 , y2 , z2 ) , то BC направляющий вектор этой прямой, поэтому из (3.45) получим:

x − x1	=	y − y1	=	z − z1	(3.46)
x2 − x1		y2 − y1		z2 − z1

(3.46) – уравнения пространственной прямой, проходящей через две заданные точки.

УГОЛ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ

Рассмотрим прямые, заданные в некоторой пдск каноническими уравнениями:

L	1	:	x − x1	=	y − y1
			m1		n1

L2 : x − x2 = y − y2 m2 n2

= z − z1 , s = (m , n , p )
				UR
					1	1	1
				1	1	1	1
		p1
=	z − z2			UR	= (m , n , p			).
	z − z2		, s
			, s
2					2	2	2
		p2

ОПРЕДЕЛЕНИЕ. Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.

UR UR

, s2 ). Если

Из определения следует, что (L1

2 ) = (s1

(L1,L 2 ) = ϕ , то

UR UR

cosϕ =

(s1, s2 )

m m + n n + p p

m 2

+ n 2

+ p 2

2 + n 2

+ p 2

L1 L 2

s1 s2

(s1,

s2 ) = 0 m1 m2 + n1

n2 + p1 p2 = 0 – условие

перпендикулярности прямых.

s s

–

условие параллельности прямых в

пространстве.

ПРИМЕР. Найти угол между прямой L1

x −1

y + 1

и прямой L

2 ,

-3

проходящей через точки A(-1,3,3)

и B (2,3, -1) .

UUUR

18 + 12

= (6,2, -3), s

= AB

(3,0, -4) cosϕ

7 ×5

Заметим, что уравнение прямой L2

имеет вид:

x + 1

y − 3

z − 3

. В данном

-4

случае ноль в знаменателе

писать принято: он означает, что направляющий

вектор прямой (и сама прямая) параллелен плоскости XOZ . Эта прямая являет-

ся результатом пересечения плоскостей

x + 1

z − 3

и y − 3 = 0 .

-4

ПРИВЕДЕНИЕ ОБЩИХ УРАВНЕНИЙ ПРЯМОЙ В ПРОСТРАНСТВЕ К КАНОНИЧЕСКОМУ ВИДУ

Рассмотрим прямую L , заданную общими уравнениями (3.42) в пространстве:

A1x + B1 y + C1z + D1 = 0A2 x + B2 y + C2 z + D2 = 0 .

Привести эти уравнения к каноническому виду можно двумя способами:

1)найти координаты какой-либо точки A( x0 , y0 , z0 ) , лежащей на L , ее направляющий вектор s и написать уравнения (3.45);

2)найти координаты двух точек, лежащих на L , и воспользоваться уравнениями (3.46).

1 способ. Координаты точки A – любое частное решение системы линейных уравнений (3.42). Эта система имеет бесконечное множество решений, так

как ранги основной и расширенной матриц rA = rA = 2 , а число неизвестных n = 3 .

s	– направляющий вектор прямой L , поэтому s n1, s n2 , где n1 = ( A1, B1,C1 )
–	нормаль плоскости α1 , а n1 = ( A2 , B2 ,C2 ) – нормаль плоскости α2 . Из опреде-

ления векторного произведения векторов следует, что тогда s n1 × n2 . Так как s – произвольный вектор, параллельный L , то будем считать, что s = n1 ´ n2 .

x + 2 y − 5z − 5 = 0

ПРИМЕР. Привести уравнения прямой к канониче-

x − y + 3z + 1 = 0

скому виду.

Найдем какое-нибудь частное решение этой системы: пусть, например,

z = 0

x + 2 y = 5

3y = 6

y = 2 x = 1 , то есть точка

A(1, 2, 0)

лежит на

− y = −1

прямой.

= (1,2,

UUR

= (1,

−1,3)

UUR

−5), n2

= n1

× n2

−5

= i

− 8 j − 3k .

−1

Таким образом,

x −1

y − 2

– канонические уравнения данной прямой.

−3

−8

2 способ. Найдем два произвольных частных решения системы уравнений, задающей прямую.

В рассмотренном примере A(1,2,0) L . Пусть теперь

							x + 2 y = 20		3y = 30 y = 10 x = 0 ,
						z = 3			3y = 30 y = 10 x = 0 ,
							x − y = −10
тогда B (0,10,3) L AB = s1 = (−1,8,3) –										направляющий вектор прямой, кото-
рый		отличается					от найденного	ранее		только знаком. Поэтому уравнения
	x −1	=	y − 2	=	z		совпадают (с точностью до знака) с уже найденными.
	−1	=		=			совпадают (с точностью до знака) с уже найденными.
	−1	8		3

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

ОПРЕДЕЛЕНИЕ. Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость.

Пусть в некоторой пдск заданы плоскость

α : Ax + By + Cz + D = 0,							R
							n = ( A, B, C )
и прямая	x − x		y − y			z − z
		=		0	=		R	= (m, n , p)
L :	0						, s		(рис. 50).
	m		n			p

R R

(n, s)

− ϕ

cos

− ϕ = sinϕ =

Am + Bn + Cp

A2 + B2 + C 2

+ n2 + p2

Рис. 50

1) α L n s

–

условие перпендикулярности прямой

и плоскости (рис. 51).

Рис. 51

R R

2) α L n

s (n, s ) = 0

Am + Bn + Cp = 0 −

– условие параллельности прямой и

α	плоскости (рис. 52).
	плоскости (рис. 52).
Рис. 52

ОПРЕДЕЛЕНИЕ ОБЩИХ ТОЧЕК ПРЯМОЙ И ПЛОСКОСТИ

Чтобы найти общие точки прямой

L :

x − x0

y − y0

z − z0

и плоскости

α : Ax + By + Cz + D = 0 , надо решить систему линейных уравнений:

Ax + By + Cz + D = 0

y − y

z − z

x − x

<<< < Предыдущая 1 2 3 4 5 6 78 / 98 9 > Следующая >>>