Добавил:

Loll384 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Омский Государственный Технический Университет

Предмет:

Математика

Файл:

nikolaeva_lineinaya_algebra_konspekt_lekciy_chast1

.pdf

Скачиваний:

Добавлен:

05.09.2020

Размер:

842.16 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

ТЕОРЕМА 2. Пусть a ,b , c – некомпланарные векторы. Тогда любой вектор d может быть представлен в виде

d = xa + yb + zc , x, y, z R , (2.2)

причем единственным образом.

Представление вектора d в виде (2.2) называется разложением его по

трем некомпланарным.

Доказать самостоятельно.

ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ. КООРДИНАТЫ ВЕКТОРА

Осью называется направленная прямая.

ОПРЕДЕЛЕНИЕ. Ортом оси l называется единичный вектор l0 , направление которого совпадает с направлением оси.

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией точки М на ось l называ-

ется основание М1 перпендикуляра, опущенного из М на l .

ОПРЕДЕЛЕНИЕ. Ортогональной проекцией вектора AB на ось l назы-

вается длина отрезка А1В1 этой оси, заключенного между ортогональными проекциями его начала и конца, взятая со знаком «+», если направление век-

тора A1B1 совпадает с направлением оси, и со знаком «–», если эти направления противоположны (рис. 8).

	B	C
		F
A	ϕ	D	ψ
		D	E
			E
A1	B1	C1(D1) F1	l
A1	B1	C1(D1) F1	E1
		Рис. 8

прl AB = A1B1 , прl CD = 0, прl EF = − E1F1 .

ОПРЕДЕЛЕНИЕ. Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).

UUUR	UUUR	3π	UUUR
		3π
ϕ = (AB, l ),	(CD, l ) =		, ψ = (EF , l )	(рис. 8).
ϕ = (AB, l ),	(CD, l ) =	2	, ψ = (EF , l )	(рис. 8).
		2

UUUR

UUUUR

UUUR

3π

пр AB

A B

cosϕ > 0, так как

ϕ − острый угол; пр CD =

cos

= 0;

1 1

UUUR

UUUUR

UUUR

cos (π −ψ ) =

UUUR

= −

cosψ < 0, такψ − тупой угол (рис.8).

прl EF

E1F1

Очевидно, проекцию вектора на ось можно найти по формуле

UUUR

прl AB =

cosϕ, ϕ = (AB,l ).

Можно показать, что проекция линейной комбинации векторов равна такой же линейной комбинации их проекций:

R	R	R	R	α , β R .
прe (α a + β b ) = α прe a + β прe b,

В частности, проекция суммы векторов равна сумме их проекций:

			R	R	R			R
			прe (a + b ) = прe a +			прe b .
Рассмотрим		прямоугольную		декартову			систему		координат ХОY. Обо-
значим	i – орт оси ОХ, j		– орт оси OY. Выберем точку A , и пусть x, y – про-
екции ее на ОХ и OY,то есть координаты этой точки (рис. 9).
Y				OA –		радиус-вектор точки A и
Y
				OA = OA1 + OA2 , но
	y							= 1 OA1 = xi.
A2		A		OA i,			i	= 1 OA1 = xi.
j	i	A1	X	Аналогично OA2 = y j OA = xi + y j
		A1		Аналогично OA2 = y j OA = xi + y j
О		x		–	разложение				OA по ортам коорди-
				–	разложение				OA по ортам коорди-
				натных осей i, j (разложение единст-
	Рис. 9			венно по теореме 1).
Аналогично в пространственной системе OXYZ									(i, j, k – орты коорди-
натных осей) (рис. 10):

OA = OB + OA3 = OA1 + OA2 + OA3 , OA1 = xi, OA2 = y j, OA3 = zk OA = xi + y j + zk

– разложение OA по ортам координатных осей (единственно по теореме 2).

Z
A3	z
	A
k
O	j A2 Y
i	y
A1
x	B

Рис. 10

Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором OA можно связать три числа x, y, z (или два числа x, y , если вектор плоский), которые являются коэффициентами разложения этого вектора по ортам координатных осей, а также являются проекциями этого вектора на координатные оси.

ОПРЕДЕЛЕНИЕ. Координатами вектора OA в любой пдск называются коэффициенты в разложении этого вектора по ортам координатных осей.

Таким образом, можно дать еще одно определение вектора.

ОПРЕДЕЛЕНИЕ. Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).

	ПРИМЕР. Если OA = 2i + 3 j + 4k ,	то	OA =(2,3,4) и наоборот, если
OB = (4,3, 2) , то OB = 4i + 3 j + 2k.
	Так как, с одной стороны, вектор –	объект, имеющий длину и направле-
ние,	а с другой, – упорядоченная тройка	чисел, то, зная длину и направле-
ние,	можно определить его координаты и		наоборот. Направление вектора

в заданной системе координат характеризуется его направляющими косину-

сами (рис. 11):

cosα = cos(a,OX ), cos β = cos(a,OY ), cosγ = cos(a,OZ ) .

Пусть a = ( x, y, z )

x2 + y2 + z2 , cosα =

, cos β =

, cosγ =

Из этих формул очевидно следует ос-

новное свойство направляющих коси-

нусов:

cos2 α + cos2 β + cos2 γ = 1.

O β

Если известны длина

и направ-

ляющие косинусы вектора, то его ко-

Рис. 11

ординаты вычисляются по формулам:

x =

cosα , y =

cos β , z =

cosγ .

Пусть AB – произвольный вектор в сис-

A( xa , ya , za )

теме OXYZ, OA,OB –

радиус-векторы

B ( xb , yb , zb )

его начала и конца,

A( xA , yA , zA ), B ( xB , yB , zB ), (рис.12).

Тогда

AB = OB − OA, OB = xB i + yB j + zB k,

Рис. 12

OA = xA i + yA j + zA k

OB − OA = ( xB − xA )i + ( yB − yA ) j + ( zB − zA )k

(см. свой-

ства

линейных

операций

над

векторами).

Таким

образом,

AB = ( xB − xA , yB − yA , zB − zA ) , то есть для определения координат вектора надо из координат его конца вычесть координаты начала.

ОПРЕДЕЛЕНИЕ. Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).

	e2	Если (e1,e2 ,e3 ) – базис, то (e2 ,e1,e3 ) –
	e2	другой базис, так как изменился поря-
		другой базис, так как изменился поря-
	e1	док следования векторов.
	e1
		ОПРЕДЕЛЕНИЕ. Базис называ-
	e3	ется прямоугольным декартовым, если
		базисные векторы взаимно перпенди-
	Рис. 13	кулярны и длина каждого равна 1.
	Такой базис принято обозначать	(i, j, k ) .

Из теоремы 2 следует, что всякий вектор a может быть разложен по базису (e1,e2 ,e3 ) , то есть представлен в виде: a = x e1 + y e2 + z e3 . Числа x, y, z называются координатами a в базисе (e1,e2 ,e3 ) .

ОПРЕДЕЛЕНИЕ. Базисом на плоскости называется любая упорядочен-

ная пара неколлинеарных векторов.

Если (e1,e2 ) – базис,

то представление вектора в виде a = x e1 + y e2

на-

зывается разложением

по базису (e1,e2 )

и x, y – координаты a

в этом ба-

зисе.

ОПРЕДЕЛЕНИЕ.

Базисом на прямой называется любой ненулевой век-

тор этой прямой.

ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ

Рассмотрим задачу: дан отрезок

AB . Найти точку D , которая делит

в заданном отношении

k :

= k (рис. 14).

Введем

прямоугольную

декартову

систему координат (пдск) OXYZ, то-

гда

A( xA , yA , zA ), B ( xB , yB , zB ).

Обозначим

OA = a, OB = b, OD = d

UUUR

R UR

Рис. 14

= d

− a, DB = b − d.

Так

как

AD DB

(лежат на

одной

прямой)

= k

то

UUUR UUUR

a + kb

AD = k DB

− a = k (b − d ) (1 + k )d

= a + kb

d =

. Переходя от это-

1 + k

го векторного равенства к равенству соответствующих координат, получим:

x =	xA + kxB	, y		=	yA + kyB	, z		=	zA + kzB	.	(2.3)

D	1 + k		D		1 + k		D		1 + k

ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k = 1, поэтому

x	=	xA + xB	, y =	yA + yB		, z		=	zA + zB	(2.4)
							ср
ср	2		ср		2			2

ЗАМЕЧАНИЕ 2. Если k < 0 ,					k ¹ -1, то точка D лежит за пределами
AB : так как AD = k DB , то при k < 0					AD −↓ DB.

В этом случае

Пусть

UUUR

k = −2

= 2

AD = −2DB (рис. 15).

Рис. 15

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ.

Скалярным произведением векторов a и b называет-

R R

ся скаляр (число), равный

× cosϕ, ϕ = (a,b).

Скалярное произведение обозначается так: (a,b) =

cosϕ

или

a ×b =

cosϕ .

Так как

cosϕ = прR a

(рис. 16) или

cosϕ = прR b ,

то (a,b) =

прR a =

прR b .

Рис. 16

СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ

1.(a,b) = (b, a) – очевидно из определения.

2.(a + b,c) = (a,c) + (b,c).

ДОКАЗАТЕЛЬСТВО:

(a + b,c) = c прcR (a + b) = c (прcR a + прcR b) = c прcR a + c прcR b = (a,c) + (b,c).

3. α (a,b) = (α a,b), α Î R.

ДОКАЗАТЕЛЬСТВО:

а) α = 0 – очевидно.

б) α > 0. αa -- a (a,b)=(αa,b)=ϕ; α =α (αa,b) = α ab cosϕ =α (a,b).

R R	R R		R R	R R	R R	R R

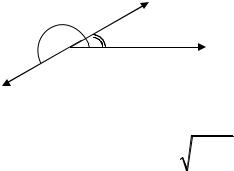
в) α < 0. В этом случае

R R

π + ϕ

α a −↓ a (α a,b) = π + ϕ;

= −α

R R

(α a,b) =

cos(π + ϕ ) =

= −α

(− cosϕ )

R R

α a

= α (a,b).

R R

4. (a, a) =

(a, a) .

Отсюда следует, что

(a, a) > 0 Û a ¹ O , (a, a) = 0 Û a = O.

Необходимым и достаточным условием перпендикулярности векторов

является равенство нулю их скалярного произведения:

5. a ^ b Û (a,b) = 0.

ДОКАЗАТЕЛЬСТВО:

а) пусть a ^ b cosϕ = 0 (a,b) = 0.

б) пусть (a,b) = 0

= 0

или

= 0 , или cosϕ = 0 .

В первом и втором случаях один из сомножителей –

нулевой вектор. Его

направление не определено, поэтому можно считать, что a ^ b . В третьем слу-

чае ϕ = π	или ϕ =	3π	, то есть a b .

2	2

Используя свойства 4 и 5, составим таблицу вычисления скалярного произведе-

ния базисных векторов i, j, k :

	Скалярное	i	j	k
	произведение
	i	1	0	0

	j	0	1	0

	k	0	0	1

Пусть в некоторой пдск a = xa i + ya

j + za k,

b = xb i + yb j + zb k . Найдем скалярное

произведение этих векторов:

R R

(a,b) = (

xa i

+ ya j

+ za k )× (

xb i

+ yb j

+ zb k ) = xa xb

+ xa yb (i, j ) + xa zb (i, k ) + ya xb ( j,i ) +

+ ya yb

R R

= xa xb + ya yb

+ za zb .

+ ya zb ( j, k ) + za xb (k,i ) + za yb (k, j ) + za zb

Таким образом, (a,b) = xa xb + ya yb + za zb (2.5)

ПРИМЕР. Найти, при каком значении x векторы a = ( x,0, 2) , b = (2,5,3)

перпендикулярны.

Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведе-

ние по формуле (2.5): (a,b) = 2x + 0 + 6 = 0 x = −3.

ПРИМЕР. Найти угол между биссектрисой

AD и медианой AM ABC ,

если A(0, −1,0), B (2,1, −4),C (−1, −3, −1).

Так как

(a,b) =

cosϕ ,

(a,b)

R R

то

cosϕ =

(2.6)

Найдем координаты векторов AD и AM . Точка M – середина BC , по-

UUUUR

этому по формулам (2.4) M

, −1, −

,0, −

По теореме о биссектрисе внутреннего угла треугольника CD = AC = k .

Чтобы найти k , вычислим длины AC и AB :

DB AB

AC = (−1, −2, −1), AB = (2, 2, −4)

UUUR

= 1 + 4

+ 1 =

= 4

+ 4

+ 16

= 2 6

UUUR

UUUR UUUR

k =

AB = 2 AC

DB = 2CD

= 2.

Разделим отрезок CB в данном отношении по формулам (2.3):

xB + 2xC

= 0, y

yB + 2 yC

= −

zB + 2zC

= −2 ,

UUUR

отсюда

D 0, −

, −2

AD =

0, −

, −2 .

UUUUR UUUR

UUUUR

UUUR

Заметим, что

Это замечание позволит нам не

(AM , AD)= (2 AM ,3AD)= ϕ .

иметь дело с дробями, так как

UUUUR

UUUR

+ 0

2 AM

= (1,0, −5), 3AD =

(0, −2, −6) cosϕ =

								π
	a - 2b		R	=1,	R	= 2,	R R
ПРИМЕР. Найти	a - 2b	, если	a	=1,	b	= 2,	(a,b)= .
								3
								3

Воспользуемся свойствами 1–4 скалярного произведения:

R R

a - 2b

= (a

- 2b)

- 4(a,b) + 4

=1 - 4 × 2 ×

+ 4 × 4 =13.

Отсюда

a - 2b

13.

ЗАМЕЧАНИЕ. Так как работа силы F по перемещению материальной точки вдоль вектора s вычисляется по формуле A = F s cosϕ , то A = (F , s ) .

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

ОПРЕДЕЛЕНИЕ. Тройка некомпланарных векторов (a,b,c), имеющих

общее начало, называется правой (левой), если с конца третьего вектора c вра-

щение первого вектора a ко второму вектору b по кратчайшему пути наблюдается против (по) часовой стрелки (рис. 17).

(a,b,c) – левая тройка,

(b, a,c) – правая тройка,

(c, a,b) – левая тройка.

Рис. 17

(i, j, k ) – правая тройка (рис. 18).

i j

Рис. 18

ОПРЕДЕЛЕНИЕ. Векторным произведением вектора a на вектор b на-

зывается вектор c , удовлетворяющий условиям:

1.	c a, c b ( c перпендикулярен плоскости векторов a и b ).
2.	Направление c таково, что тройка (a,b,c) – правая.

	R		R	R	R R
3.	c	=	a	b
					sinϕ, ϕ = (a,b).

Векторное произведение обозначается так: c = a × b или c = a, b .

ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.

Sпар− ма = a ´ b .

Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.

Заметим, что

R R

sin2 ϕ =

(1 - cos2 ϕ ) =

cos2 ϕ =

R R

a ´ b

- (a,b)

Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле

R R
	=	R	2	R	2	R R	2
		R	2	R	2	R R	2
a × b		a		b		− (a,b)	.	(2.7)

ПРИМЕР. Найти площадь параллелограмма, построенного на векторах a = (-1, 2, 4), b = (0, -1,1).

= 21;

R R

= 2; (a, b ) = 2 .

По формуле (2.7):

S =

a ´ b

21× 2 - 4

38.

ЗАМЕЧАНИЕ 2. Направление вектора c можно также (кроме п.2) опре-

делить по правилу винта: направление вектора

совпадает с направлением

поступательного движения винта в правой резьбой при вращении его в

сторону поворота первого вектора a			ко второму вектору b по кратчайшему
пути (рис. 19).
		a	R	R	× b
		a	c = a		× b
		b			b
		b
					a
R	R	× b
c = a		× b

Рис. 19

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>