5. Непрерывные случайные величины.

Функция распределения. Плотность распределения.

Числовые характеристики непрерывных случайных

Величин

Случайная величина непрерывного типа может принимать все значения из некоторого интервала числовой оси. Например, стреляя из одного и того же орудия на одном и том же прицеле и при не измененных условиях, мы наблюдаем «рассеивание» снарядов. Расстояние места падения снаряда от места его вылета есть случайная величина, получающая различные численные значения при различных выстрелах. Другим примером может служить колебание напряжения в сети в определенных пределах в зависимости от неподдающихся предварительному учету случайных обстоятельств.

Непрерывная случайная величина имеет бесчисленное множество возможных значений, сплошь заполняющих некоторый промежуток, поэтому невозможно составить ряд распределения такой «случайной» величины. Однако различные области возможных значений имеют определенную вероятность.

Для количественной характеристики непрерывной случайной величины используется функция распределения

F(х) = Р (Х < х),

которая представляет собой вероятность события Х < х , где х – некоторая текущая переменная.

Функцию F (x) называют интегральной функцией распределения. Функция распределения полностью характеризует случайную величину с вероятностной точки зрения, т.е. является одной из форм закона распределения.

Отметим свойства функции распределения.

1. Функция распределения F(x) является неубывающей функцией, т.е. при x₂ > x₁ выполняется неравенство F (х₂) > F (x₁).

2. Значения интегральной функции распределения находится в пределах от 0 до 1. Действительно, F ( - ) = 0 как вероятность невозможного события, а F(+) = 1 как вероятность достоверного события .

3. Вероятность того, что случайная величина Х заключена в пределах

х₁ < Х < х₂,

равна разности значений интегральной функции распределения в верхнем и нижнем пределах, то есть

P (x₁ < X < x₂) = F (x₂) - F(x₁).

В справедливости этого легко убедиться, рассматривая события

А = {X < x₂}, B = {X < x₁}, С = {x₁ < X < x₂}.

Очевидно , что А = В + С и события В и С несовместны, поэтому

Р(А) = Р(В) + Р(С).

Но

Р(А) = Р(Х < x₂) = F(x₂),

Р(B) = Р(Х < x ₁) = F(x ₁),

Р(C) = Р(x₁ < X < x₂ ).

Таким образом,

Р(x₁< X < x₂) = F(x₂) –F(x₁).

4. Если Х – непрерывная случайная величина с функцией распределения F(x), то вероятность того, что Х примет заранее заданное значение, равна нулю.

Действительно,

.

Для непрерывных случайных величин равенство нулю вероятности не означает ,что это событие невозможное.

Графиком интегральной функции распределения вероятностей является не убывающая кривая, непрерывная или имеющая конечное число точек разрыва первого рода.

Для характеристики распределения вероятностей непрерывной случайной величины вводится понятие плотности распределения вероятностей по аналогии с плотностью распределения массы внутри сплошного распределения массы внутри сплошного материального тела:

или

Если функция F(x) непрерывна и дифференцирована, то

f(x) = F(x),

поэтому имеет место соотношение

,

из которого становится ясным термин «интегральная функция распределения».

Перечислим основные свойства плотности распределения вероятностей f(x).

1. Поскольку F (x) неубывающая функция, то f (x)  0. Геометрически это означает, что график плотности вероятности f (x), который называется кривой распределения, лежит над осью абсцисс.

2. Так как интегральная функция распределения вероятностей при

  < х < + ,

удовлетворяет неравенствам

0< F(x) < 1,

то

.

Это означает, что для кривой распределения ось абсцисс является асимптотой.

3. Поскольку

,

и

F(+) = 1,

то

.

Геометрически это означает, что полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

В частном случае ,если множество значений непрерывной случайной величины принадлежит конечному интервалу (а, b), то интеграл от плотности вероятности f (x), взятый в интервале (а, b), равен 1:

Действительно, в этом случае

F( b) = F( X< b) =1?

так как событие Х <b является достоверным, и

F (a) = P (X< a) = 0,

так как событие Х < a является невозможным.

Если Х и Y - независимые случайные величины, имеющие плотности распределения f₁ (x) и f₂ (x) соответственно, то плотность распределения суммы Z = X +Y находится по формуле

,

т.е. плотность распределения суммы независимых случайных величин есть свертка плотностей распределения слагаемых.

Во многих вопросах практики нет необходимости характеризовать случайную величину плотностью, а достаточно указать только отдельные числовые параметры, которые характеризуют наиболее существенные особенности распределения.

Среди числовых характеристик случайных величин наиболее часто применяются математическое ожидание и дисперсия.

Математическое ожидание характеризует положение случайной величины на числовой оси, то есть указывает некоторое среднее значение, около которого группируются всевозможные значения случайной величины.

Для непрерывной случайной величины математическое ожидание М(Х) выражается формулой

+

М(Х) =  х f (x) dx.

-

Дисперсия случайной величины есть характеристика рассеивания, разбросанности значений случайной величины около её математического ожидания. Для вычисления дисперсии непрерывной случайной величины служат формулы

,

или

.

5.1. Случайная величинаXзадана функцией распределения

Вычислить вероятности попадания случайной величины Xв интервалах (1,5; 2,5) и (2,5; 3,5).

Решение. По определению функция распределениявероятностей случайной величиныXявляется вероятностью событияX <x:

F(x) = P(X < x).

Поскольку

P(X < β) = P(X < α) + P(α  X < β),

то

P(α  X < β) = F(β) - F(α).

Вычислим значения функции распределения:

F(1,5) = (1,5 - 1)/2 = 0,25,

F(2,5) = (2,5 - 1)/2 = 0,75,

F(3,5) = 1.

Тогда

P(1,5 <X <2,5) = 0,75 - 0,25 = 0,5;

P(2,5 <X <3,5) = 1 - 0,75 = 0,25.

5.2.Случайная величинаXзадана функцией распределения

Найти вероятность того, что в результате четырех испытаний случайная величина Xровно три раза примет значения из интервала (0,3; 0,7).

Решение.Случайная величинаXравномерно распределена на отрезке [0,1]. Для решения задачи применяется схема Бернулли из четырех испытаний с вероятностью успеха в одном испытании, равномp. Успехом в одном испытании будет попадание значения случайной величиныXв интервал (0,3; 0,7). Найдемp:

p = P(0,3<X<0,7)=F(0,7)-F(0,3)=0,7-0,3=0,4.

По формуле Бернулли:

P₄(3) =C(0,4)³·0,6 = 0,1536.

5.3.Функция распределения случайного времениXбезотказной работы прибора имеет вид

где T > 0. Найти:

а) вероятность безотказной работы прибора в течение времени t  T;

б) плотность распределения случайной величины X;

в) математическое ожидание М(X) и дисперсию D(X) случайной величины X.

Решение.

а) Вероятность безотказной работы прибора в течение времени t  TозначаетP(0 X T).Используя функцию распределения, найдём

P(0 X T) = F(T)-F(0)=1-e^-10,63.

б) Плотность распределения вероятностей определяется по аналогии с определением плотности массы в точке:

Таким образом,

в) Математическое ожидание и дисперсия являются числовыми характеристиками случайных величин.

По определению математического ожидания получим

Воспользуемся более удобной формулой для нахождения дисперсии:

5.4.Известно, что вероятность выхода из строя электронной лампы в течениеxдней, с точностью до величины порядка малости более высокого, чемx, равнаk·xнезависимо от величиныxдней, которые лампа проработала до интервала времениx.Какова вероятность выхода из строя лампы в течениеlдней?

Решение.Введем в рассмотрение случайную величинуXдней – промежуток времени, в течение которого лампа теряет работоспособность. Функция распределения

F(x) = P(X < x),

означает вероятность того, что лампа выйдет из строя за время, меньшее xдней. Если мы найдемF(x), тоF(l) будет означать вероятность выхода из строя лампы в течениеlдней (т.е.X<l).

Для нахождения F(x) составим уравнение. Вероятность

P(x + x > X > x)

– это вероятность события С, состоящего в том, что промежуток времени, в течение которого лампа перегорит, большеxи меньшеx +x. Это событиеСравно произведению (одновременному выполнению) двух независимых событий:

А = {лампа не перегорит за времяxдней} = {X x}

и

В = {лампа перегорит за времяxдней}.

По условию P(B) =k ·x. ПосколькуC =A·B, то

P(C) = P(AB) = P(A)·P(B),

т.е.

P(x + x>X>x) = P(X>x)·k·x = [1 - F(x)]k·x.

С другой стороны,

P(x + x >X > x) = F(x + x) - F(x).

Отсюда следует:

Пусть x0, тогда получим дифференциальное уравнение с разделяющимися переменными

Проинтегрируем это уравнение:

При x = 0 получим

F(0) = 1 -С·e⁰ = 0,

т.е. С = 1. Окончательно

F(x) = 1 - e^-kx,

тогда вероятность выхода из строя лампы в течение lдней будет равна

1 - e^-lx.

Распределение вида

F(x) = 1 - e^-kx, (k  0)

называется показательным (экспоненциальный закон). Срок службы элементов электронной аппаратуры часто описывается таким законом распределения.

5.5. Вычислить математическое ожидание и дисперсию случайной величины Х, имеющей равномерное распределение на отрезке [a, b].

Решение. Если известно, что возможное значение случайной величины Х лежит в пределах некоторого определенного интервала и, кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (то есть обладают одной и той же плотностью вероятности ), то такая случайная величина Х распределена по закону равномерной плотности. Плотность вероятности в этом случае имеет вид:

Вычислим математическое ожидание

и дисперсию по формуле

где

поэтому

5.6.Вычислить математическое ожидание и дисперсию случайной величины Х, имеющей показательное распределение с параметром .

Решение. Показательное распределение - это распределение с плотностью вероятности

f(x)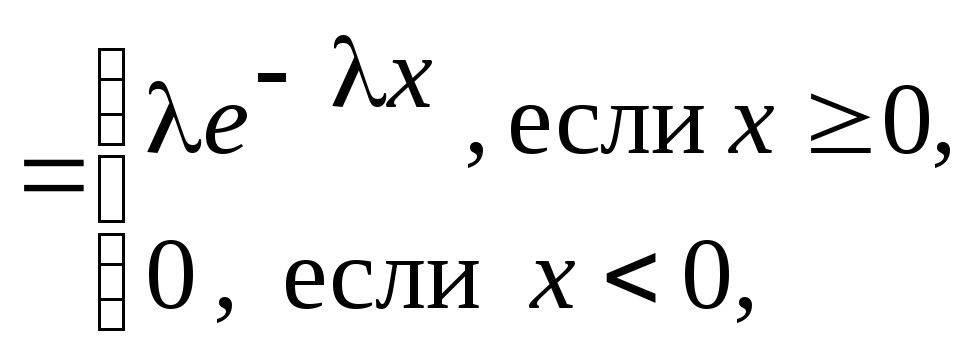

где - параметр распределения. Поэтому математическое ожидание имеет вид

M (X) = .

Для нахождения дисперсии случайной величины найдем математическое ожидание квадрата этой случайной величины:

M(X²) = .

Тогда дисперсия случайной величины Х будет равна

5.7. Вычислить математическое ожидание и дисперсию распределения Релея с параметром .

Решение. Плотность вероятности случайной величины Х, распределенной по закону Релея с параметром >0, имеет вид

.

По определению математического ожидания для непрерывной случайной величины Х имеем

,

(при вычислении этого интеграла применяется замена переменной

затем применяется интегрирование по частям).

Дисперсия случайной величины Х вычисляется по формуле

D(X) = M(X²) – [M (X)]²,

таким образом, дисперсия случайной величины X равна

5.8. Вычислить математическое ожидание и дисперсию случайной величины Х, распределенной по нормальному закону.

Решение. Нормальный закон распределения характеризуется плотностью вероятности вида:

Вычислим математическое ожидание:

Применяя замену переменной

t= (x - a) (δ),

имеем:

Первый из двух интегралов равен нулю. Второй представляет собой интеграл Эйлера – Пуассона:

.

Следовательно,

M (X) = a.

Параметр а в нормальном распределении представляет собой математическое ожидание случайной величены Х и называется центром рассеивания.

Вычислим дисперсию случайной величины Х:

После замены переменной

t= (x - a)/(δ)

приходим к интегралу

.

Интегрируя по частям получим:

.

Первое слагаемое в скобках равно нулю:

(здесь применялось правило Лопиталя).

Второе слагаемое в скобках, как мы видели выше, равно , поэтому

D (X) = σ ².