___________________________________________Тема 7. Теория___

Тема 7. Определенные и несобственные интегралы Определенный интеграл

Введение понятия определенного интеграла связано с решением практической задачи – вычисление площади криволинейной трапеции.

Пусть на отрезке задана непрерывная функция, для определенности. Найдем площадь, ограниченную осью ОХ, прямыми и линией. Можно также говорить о площадипод кривой или оплощади криволинейной трапеции.

Для этого разобьем трапецию произвольным образом на частичные трапеции линиями, параллельными ОУ: , а затем заменим каждую прямоугольником со сторонойи высотой, где-произвольно выбранная на частичном отрезке точка.

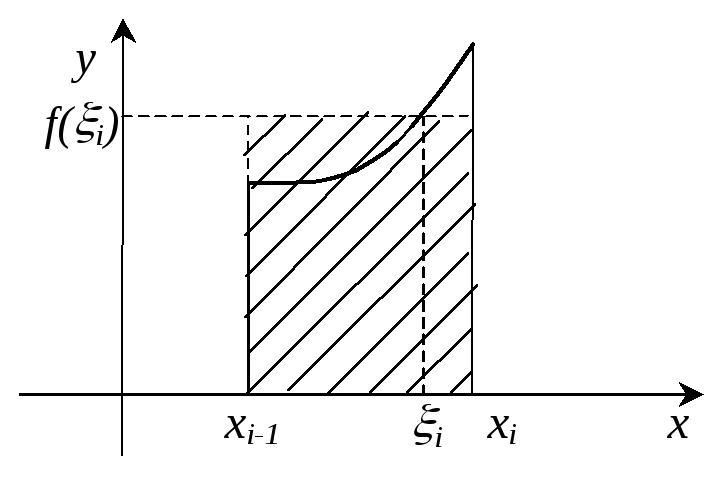
Составим сумму площадей всех прямоугольников, она будет приближенно равна площади всей криволинейной трапеции: . Такая сумма называетсяинтегральной. Очевидно, будет тем более точно определять площадь криволинейной трапеции, чем на большее число частичных трапеций будет разбита исходная криволинейная трапеция. А прис условиемэти площади совпадут.

 Если существует конечный предел интегральной суммы , при(), который не зависит от способа разбиения области на частичные отрезки и выбора точек, то он называетсяопределенным интегралом функции на отрезке [a, b ] и обозначается

.

Здесь: f(x) – подинтегральная функция, x – переменная интегрирования, – нижний ,– верхний пределы интегрирования.

 - Несмотря на сходство в обозначениях и терминологии, определенный и неопределенный интегралы существенно различные понятия: если - представляетсемейство функций, то -определенное число. 

 - Заметим, что не имеет значения, какой буквой обозначена переменная интегрирования, т.к. смена обозначений не влияет на интегральную сумму

.

Свойства определенного интеграла.

1 - если поменять местами верхний и нижний пределы интегрирования, определенный интеграл поменяет знак.

2 - интеграл с одинаковыми пределами интегрирования равен нулю по определению.

3 ;

.

Аналогичные свойства есть и у неопределенного интеграла. Они показывают, что интегрирование – линейная операция и может быть распространена на любое конечное число слагаемых: .

4 Свойство аддитивности. Если - функция, интегрируемая на

и , где, то она интегрируема наи

Иными словами, отрезок интегрирования можно разделить на части какой-либо точкой и интеграл по всему отрезку заменить суммой интегралов по двум полученным отрезкам.

5 Свойство алгебраической площади. Определенный интеграл есть число того же знака, что и подынтегральная функция. То есть, при вычислении площадей с помощью определенного интеграла можно получить отрицательную площадь.

 Теорема-о среднем значении функции на отрезке.

Если непрерывна на отрезке (), то на этом отрезке существует хотя бы одна точка (), такая, что функция принимает в ней своесреднее значение

.

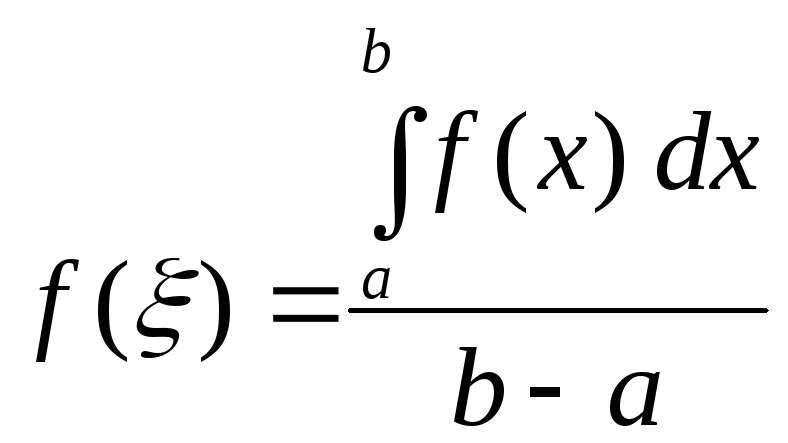Г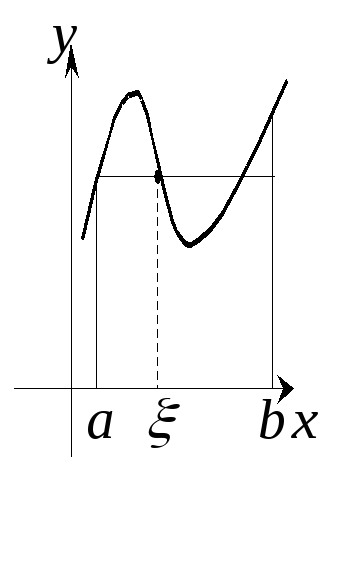еометрический смысл теоремы: пусть , тогда существует, по крайней мере, одна точка, такая, что площадь криволинейной трапеции, ограниченной сверху непрерывной кривойбудет равна площади прямоугольника с тем же основанием (b – a) и высотой, равной :

.