Примеры к теореме 1

• Рассмотрим квадратный многочлен и найдем его корни.дискриминант. Отрицательный дискриминант означает, что многочлен имеет комплексные корни.. Введеммнимую единицу . По общему правилу корни- комплексно-сопряженные числа. Можно записать их и так:. Таким образом, многочлен второго порядка имеет два корня.

• Рассмотрим многочлен 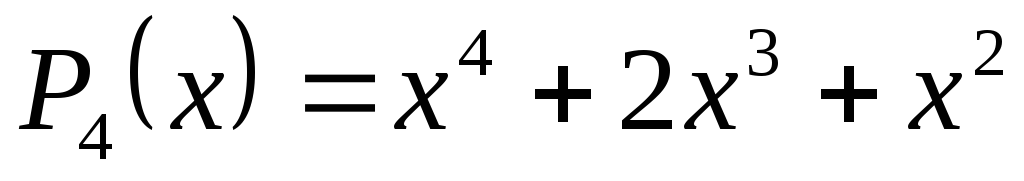и определим его корни.

	После алгебраических преобразований ясно, что многочлен четвертого порядка имеет два корня и два корня. Такие корни называютсякратными. В данном случае кратность каждого из корней - два.

 - Обратите внимание! Кратность корня указывается степенью сомножителя, из равенства нулю которого он получается.

 Теорема 2.Многочленn-го порядка можно представить в виде произведения ("разложить по корням"):

,

где -действительные корни многочлена; -кратность соответствующего действительного корня;

- квадратный трехчлен с дискриминантом, т.е. имеющий пару комплексно-сопряженных корней; - кратность каждого комплексного корня.

Примеры к теореме 2

• Разложить по корням многочлен: .

	Приравняем многочлен нулю и найдем его корни.
	Корни действительные, разные.
	Разложение по теореме 2. 

 Разложить по корням многочлен: .

;	Приравняем многочлен нулю и найдем его корни (по известной формуле разности кубов).
	Первый корень – из равенства нулю первого сомножителя. Корень действительный. Еще два комплексно-сопряженных корня - из равенства нулю второго сомножителя.
	Разложение по теореме 2. 

 Разложить по корням многочлен: .

;	Простое применение алгебраических преобразований: вынесение общего множителя за скобки и разложения по формуле разности
квадратов позволяют сразу определить корни и получить разложение многочлена. Все корни действительные. Корень имеет кратность 4,и− однократные, простые.
	Разложение по теореме 2. 

Разложение правильных рациональных дробей

на сумму простейших дробей

Любая рациональная дробь может быть представлена как сумма многочлена (целой части) и элементарных дробей. Под элементарными дробями понимают дроби следующих четырех видов:

(а)	(б)	(в)	(г)
Здесь А, В– const			;

 Теорема.Правильную несократимую рациональную дробь можно представить в виде суммы элементарных дробей, вид и количество которых зависит от вида и количества корней многочлена, стоящего в знаменателе этой дроби.

Пусть знаменатель дроби разложен по корням

,

и среди его корней нет совпадающих с корнями числителя – дробь несократима. Приведем таблицу соответствия сомножителей в разложении знаменателя (т.е. его корней) и элементарных дробей в представлении рациональной дроби.

Сомножитель в разложении знаменателя	Соответствующая ему сумма элементарных дробей
,
Действительному корню кратности соответствует ровноштук элементарных дробей вида (а) и (б).
,
Паре комплексно-сопряженных корней кратности соответствует ровноштук элементарных дробей вида (в) и (г).