2. Метод интегрирования по частям

Исходная формула интегрирования по частям:

 -

Основная идея метода интегрирования по частям: разбить подынтегральное выражение заданного интеграла на части итаким образом, чтобы интегралоказалсяпроще исходного.

Характерным в этом способе интегрирование есть то, что существует класс функций под знаком интеграла, для которого разбиение на части вполне предопределено. Это произведение трансцендентных функций на многочлен. Пусть - многочленn-го порядка. Например, - линейный,- квадратный, и т. д.

Схема разбиения на части подинтегральной функции зависит от вида трансцендентной части.

 В первом случае для экспоненты e ^αx и тригонометрических функций sin αx и cos αx () в качестве частиU(x) выбирается многочлен P_n (x), так как при дифференцировании степень многочлена понижается на единицу.

Исходный интеграл	Разбиение на части	По формуле
		- степень многочлена понижается на единицу.

После однократного интегрирования по частям получают интеграл того же вида, но с более низкой степенью многочлена. После n-кратного интегрирования по частям, когда от многочлена n-го порядка остаётся только константа, приходят к интегралам вида ,,, сводящимся к табличным умножением на α под знаком дифференциала.

 Во втором случае учитывается, что многие трансцендентные функции при дифференцировании превращаются в степенные и, выбирая в качестве части U(x) трансцендентную функцию, несмотря на повышение степени многочлена при интегрировании, интеграл превращается в интеграл от рациональной функции.

Исходный интеграл	Разбиение на части	По формуле
		; =.
(и другие обратные тригонометрические функции).

Примеры

Интегрирование по частям.

 ==	Разбиваем интеграл на части в соответствии с рекомендациями (первый случай).
=	По формуле интегрирования по частям.
==.	Алгебраические преобразования приводят к окончательному ответу.

 ==		Разбиваем интеграл на части в соответствии с рекомендациями (второй случай).
=		По формуле интегрирования по частям.
= =	Для вычисления интеграла применяем "внесение под знак дифференциала":  

 Метод интегрирования по частям можно применять совместно с методом замены переменных.

	Заменяем переменную x на t 2, −по формуле понижения степени.
		Полученный интеграл разбиваем на сумму двух интегралов. Первый – табличный: , второй вычисляем по частям.
=		Разбиваем интеграл на части в соответствии с рекомендациями.
			По формуле интегрирования по частям. 

3. Интегрирование рациональных дробей

Подрациональной дробьюпонимается отношение двух многочленов

.

	если , то рациональная дробьнеправильная , в ней можно выделить целую часть – многочлен степени (m – n). Выделяют целую часть путем деления многочлена на многочлен или другими алгебраическими преобразованиями.
	если , то рациональная дробьправильная.

Во многих практических задачах рассматривается интеграл от рациональной дроби , для нахождения которого рассмотрим вначале некоторые свойства многочленов.

Некоторые сведения из теории комплексных чисел

и действительных многочленов

Справка о комплексных числах.

Комплексное число: , комплексно-сопряженное ему число(или наоборот). Здесь- действительные числа,-мнимая единица. Очевидно, что и т.д. Можно убедиться, что.

• Действительный многочлен (полином):

,

где - коэффициенты при степеняхх, действительные числа.

, - линейный,- квадратный и т.д.

• Каждое число , которое обращает многочлен в ноль:, называется корнем этого многочлена. Или: корни многочлена это решения уравнения.

Теоремы о действительных многочленах.

 Теорема 1.Многочленn-го порядка имеет ровноnкорней, которые могут быть как действительными, так и комплексными числами.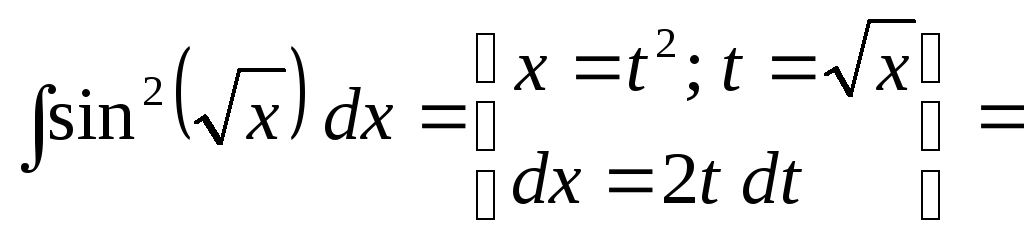