3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры

Бинарные отношения и их свойства описаны в предыдущем (втором) вопросе.

Матрица смежности описана в вводном (нулевом) и предыдущем (втором) вопросах.

Граф отношения описан в предыдущем (втором вопросе).

Отношение эквивалентности

Отношение эквивалентности (смежности) — бинарное отношение, обладающее свойствами рефлексивности, симметричности и транзитивности.

Если на множестве задано отношение , то множество разбивается на классы эквивалентных между собой элементов, которые называются классами эквивалентности (сам процесс разбиения множества на классы эквивалентных элементов называется факторизацией). В силу свойства транзитивности любые два класса эквивалентности либо совпадают, либо не пересекаются. Каждый класс эквивалентности можно рассматривать как один элемент нового множества — множества классов эквивалентности. Это множество классов эквивалентности называется фактор-множеством множества по отношению эквивалентности и обозначается . Так как классы эквивалентности не пересекаются, то каждый из этих классов однозначно определяется указанием любого его элемента.

Примеры:

1. Отношение сравнимости по модулю , заданное на множестве целых чисел, является отношением эквивалентности. Фактор-множество по этому отношению называется группой вычетов множества целых чисел по модулю и обозначается или (под понимается множество всех целых чисел, делящихся на : 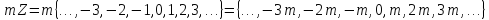). Каждый класс смежности — это множество целых чисел, которые дают одинаковый остаток от деления на 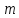, его можно задать любым его представителем, например, можно писать , но под каждым из этих чисел понимать не только его, но и весь класс смежности, к которому оно принадлежит. В частности, — это фактор-множество множества всех целых чисел по подмножеству чётных чисел, 0 означает множество всех чётных чисел (один класс смежности), 1 — множество нечётных чисел (второй класс смежности).

2. Отношение «иметь тот же возраст», заданное на множестве всех людей, есть отношение эквивалентности. «Эквивалентные» люди принадлежат к одной и той же возрастной группе. Фактор-множество — номера годов.

3. В множестве всех студентов страны можно рассмотреть отношение принадлежности одному учебному заведению. Тогда эквивалентны студенты одного учебного заведения, а фактор-множество — множество этих учебных заведений. Среди студентов одного вуза можно рассматривать отношения принадлежности одному факультету или принадлежности одному курсу, или обучения в одной группе. В этих случаях классы эквивалентности — это студенты одного факультета, или одного курса, или одной группы, а фактор-множества — множество факультетов, или множество курсов, или множество групп этого вуза (каждую группу можно упомянуть, указав, например, её старосту).

4. В множестве дней одного года можно рассмотреть отношение принадлежности одному месяцу или отношение принадлежности одному дню недели. Тогда классы эквивалентности — это дни одного и того же месяца или дни, приходящиеся на один день недели, а фактор-множества — это 12 месяцев или 7 дней недели, то есть множество из семи элементов: понедельника, вторника, …, воскресенья.

Отношение эквивалентности можно интерпретировать как отношение достижимости на неориентированном графе. Тогда классам эквивалентности будут соответствовать компоненты связности графа: любые вершины из разных компонент связности не достижимы друг из друга, а вершины одной компоненты связности достижимы. Фактор-множеством является множество компонент связности.

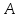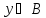Напомним, что отображением множества в множество называется сопоставление каждому элементу множества некоторого элемента из множества , то есть функция , сопоставляющая каждому элементу некоторый элемент : ; при этом называется образом элемента , а — прообразом элемента .

Отображение называется мономорфизмом, или инъекцией, или отображением «в», если у каждого элемента имеется не более одного прообраза.

Отображение называется эпиморфизмом, или сюръекцией, или проекцией, или отображением «на», если у каждого элемента имеется хотя бы один прообраз.

Отображение называется изоморфизмом, или биекцией, или взаимно однозначным соответствием, если оно является одновременно и сюръекцией, и инъекцией. Иными словами, это отображение, при котором у каждого имеется прообраз, причём только один (таким образом, при таком соответствии существует и обратное соответствие, обозначаемое : , которое каждому элементу сопоставляет его прообраз при отображении : ).

Два множества и называются эквивалентными, или равномощными (что записывается символом ), если между ними можно установить взаимно однозначное соответствие (грубо говоря, эквивалентные множества — это такие, у которых одинаковое число элементов; это понятие позволяет сравнивать даже бесконечные множества).

Говорят, что множество имеет меньшую мощность, чем множество , а множество — большую мощность, чем множество , если не существует биекции между и 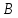, но существует биекция между и некоторым собственным подмножеством множества .

Мощность множества — символ, который сопоставляется всем множествам одинаковой мощности. Обозначение мощности множества или («двойное абстрагирование») или какой-нибудь греческой буквой, например, . В частности, мощностью конечного множества считается число его элементов. Например, если — множество клеток шахматной доски, то , а если — множество дней недели, то .

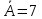Справедлива теорема Ф. Бернштейна «о трихотомии»: для любых двух множеств с мощностями и соответственно обязательно выполняется одно из 3 соотношений: (то есть любые два множества сравнимы по количеству их элементов).

Очевидно, что отношение эквивалентности множеств обладает всеми свойствами понятия эквивалентности:

1. .

2. Если , то .

3. Если и , то .

Счётные множества — множества, равномощные с натуральным рядом, то есть с множеством ; их мощность обычно обозначается символом 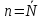. Иными словами, счётные множества — это те множества, элементы которых можно расположить в одной последовательности (индекс и есть то натуральное число, которое сопоставляется элементу счётного множества). Например, множество всех чётных чисел счётно; соответствующая биекция 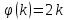, или . Интересно, что множество всех рациональных чисел тоже счётно (напоминаем, что рациональным числом называется отношение двух целых чисел 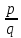). Иными словами, справедлива теорема: .

Доказательство. Запишем сначала все дроби, у которых сумма числителя и знаменателя равна 2 (такое число одно: ), затем те, у которых сумма числителя и знаменателя равна 3 (то есть ), затем те, у которых она равна 4 (), следующие 4 дроби таковы: , и так далее. В этой последовательности, очевидно, появятся все положительные дроби (так как у каждой дроби есть некоторая сумма числителя и знаменателя), но каждая дробь появится бесконечно много раз (некоторые дроби сократимы). Однако мы можем удалить из получившейся последовательности все сократимые дроби, и тогда получим последовательность всех положительных рациональных чисел, в которой каждое число встречается только один раз. Чтобы расположить в одну последовательность все рациональные числа — положительные, отрицательные и 0, составим из последовательности новую последовательность по правилу: . В последовательности расположены все рациональные числа, причём каждое — по одному разу, а это означает, что их множество счётно.

Кроме того, следуя следующим простым шагам, можно построить дерево из всех положительных рациональных дробей:

• Начинаем с в вершине дерева.

• Значение нижнего левого узла относительно текущего : .

• Значение нижнего правого узла относительно текущего : .

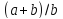Рисунок 19

Мощность континуума — мощность множества всех вещественных чисел . Также термин «континуум» может обозначать само множество вещественных чисел , или даже любое континуальное множество (любое бесконечное множество, равномощное множеству действительных чисел).

Пример множества, имеющего мощность континуума: множество всех точек отрезка ; его мощность обозначается символом .

Теорема. , то есть множество точек отрезка 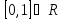несчётно, но имеет счётное подмножество (таким образом, точек на отрезке принципиально больше, чем натуральных чисел).

Доказательство. Предположим, что подмножество точек отрезка счётно. Осталось доказать, что не существует биекции этого отрезка на счётное множество. Предположим противное: что такая биекция отрезка существует, то есть все точки отрезка можно расположить в одну последовательность 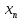. Каждое число отрезка можно записать в виде бесконечной десятичной дроби, причём однозначно, если исключить записи, в которых после некоторой цифры все последующие цифры равны 9. Обозначим последовательные десятичные цифры числа через , то есть , где означает -ую цифру числа . Составим бесконечное десятичное число , каждая цифра которого отличается на 1 от соответствующего десятичного знака числа , то есть число (знак «» или «» перед единицей можно выбирать произвольно, если только соответствующая цифра 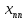не является нулём или девяткой). Это число принадлежит отрезку и поэтому должно совпадать с одним из чисел , например . Но оно не может совпадать с 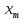, так как десятичная цифра с номером у чисел и — разная (они отличаются на единицу по построению). Полученное противоречие доказывает, что предположение неверно, и теорема доказана.

Следствия.

1. Все отрезки имеют мощность континуума. Действительно, биекция между и задаётся формулой .

2. Любой интервал имеет мощность континуума. Для доказательства достаточно установить биекцию между и 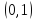. Построим её так:

3. Множество точек любой окружности имеет мощность континуума: очевидна биекция между окружностью и полуоткрытым интервалом , а по предыдущему существует биекция между и .