Циклическая группа

Теорема. Пересечение любого множества подгрупп данной группы само является подгруппой этой группы.

Пусть — произвольное непустое подмножество группы . Рассмотрим всевозможные подгруппы , которые содержат в качестве подмножества. Одной из них будет, в частности, сама группа (уже было сказано о том, что у каждой структуры есть две несобственные подструктуры — сама структура и нейтральный элемент). В силу предыдущей теоремы пересечение всех таких подгрупп будет какой-то подгруппой , которая называется подгруппой, порождённой множеством , и обозначается .

Группа — 1) подгруппа исходной группы , порождённая множеством , 2) результат пересечения всех подгрупп исходной группы , содержащих в качестве подмножества.

Циклическая группа — 1) подгруппа исходной группы , порождённая элементом (то есть состоит из одного элемента — ), 2) группа, которая может быть порождена одним элементом .

Мультипликативная группа (аддитивная группа ) называется циклической, если она состоит из всех целых степеней (всех целых кратных) одного элемента , то есть

Теорема. Циклическая группа , порождённая элементом , состоит из всех целых степеней (целых кратных) элемента (все степени принадлежат группе ).

Если группа совпадает с одной из своих циклических подгрупп (то есть состоит из степеней одного из своих элементов), то сама эта группа называется циклической, а элемент, из степеней которого состоит циклическая группа, — её образующим.

Теорема. Всякая подгруппа циклической группа сама циклическая.

Всякая циклическая группа абелева (коммутативная), так как степени одного и того же элемента коммутируют между собой.

Примеры:

1. Аддитивная группа — циклическая. Её образующий элемент — число (всякое число кратно числу 1). Это конечная группа.

2. Аддитивная группа — циклическая. Её образующий элемент — число (всякое число кратно числу 1). Также можно выбрать в качестве образующего число . Это бесконечная группа.

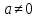3. Мультипликативная группа степеней числа — циклическая.

4. Группа, элементами которой являются корни -ой степени из 1 в множестве комплексных чисел с групповой операцией умножение, является циклической. Действительно, это конечная группа -ого порядка. Её элементы , .

Декартово произведение групп

Прямое (декартово) произведение групп — новая группа, обозначаемая , элементами которой служат наборы (или, что то же самое, кортежи) элементов из данных групп. означает, что , причём , , а групповая операция «» состоит в том, что, если , то .

Это, действительно, группа, так как роль нейтрального элемента играет кортеж , где — нейтральный элемент -ой группы, а обратные элементы задаются формулой (очевидно, что ).

— -я степень группы означает -кратное умножение её самой на себя.

Пример. — абелева группа, состоящая из двух элементов 0 и 1 с групповой операцией сложения по модулю 2 «». Поэтому состоит из последовательной длины символов 0 или 1 с поэлементным сложением по модулю 2. Например, в : . Заметим еще, что в для любого элемента справедливо равенство , так что противоположный (обратный) элемент для любого элемента равен самому этому элементу: .