
- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
Аналогично
простым числам простые элементы в кольце
 имеют специальное название.
имеют специальное название.
Приводимый
над полем многочлен
 — многочлен
— многочлен
 в кольце
в кольце
 ,
для которого выполняется
,
для которого выполняется
 для подходящих непостоянных многочленов
для подходящих непостоянных многочленов
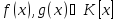 .
В противном случае
.
В противном случае
 называется неприводимым над
называется неприводимым над
 .
.
Замечание.
Приводимость или неприводимость данного
многочлена существенно зависят от поля
 .
.
Примеры.
-
Многочлен
 неприводим над полем
неприводим над полем
 ,
но приводим над полем
,
но приводим над полем
 :
:
 .
. -
Многочлен
 неприводим над полем
неприводим над полем
 ,
неприводим над
,
неприводим над
 ,
но приводим над
,
но приводим над
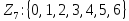 .
.
Действительно, в
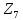 — 3 и 4 — корни многочлена
— 3 и 4 — корни многочлена
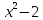 :
:




Замечание.
Из равенства
 ясно, что линейные многочлены (то есть
первой степени,
ясно, что линейные многочлены (то есть
первой степени,
 )
неприводимы над любым полем.
)
неприводимы над любым полем.
Над
полем
 (комплексные числа) неприводимы только
линейные многочлены (вспомним основную
теорему алгебры: любой многочлен имеет
хотя бы один корень, вещественный или
комплексный, откуда следует, что любой
многочлен в
(комплексные числа) неприводимы только
линейные многочлены (вспомним основную
теорему алгебры: любой многочлен имеет
хотя бы один корень, вещественный или
комплексный, откуда следует, что любой
многочлен в
 раскладывается на линейные множители).
раскладывается на линейные множители).
Над
полем
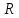 (вещественные числа) неприводимы, кроме
линейных, квадратные многочлены с
отрицательным дискриминантом.
(вещественные числа) неприводимы, кроме
линейных, квадратные многочлены с
отрицательным дискриминантом.
Над
полем
 (рациональные числа) существуют
неприводимые многочлены любой степени.
(рациональные числа) существуют
неприводимые многочлены любой степени.
Утверждение.
Любой непостоянный многочлен
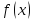 в
в
 можно представить в виде произведения
константы
можно представить в виде произведения
константы
 и
неприводимых многочленов с единичными
старшими коэффициентами. Это разложение
единственно с точностью до порядка
множителей.
и
неприводимых многочленов с единичными
старшими коэффициентами. Это разложение
единственно с точностью до порядка
множителей.
Замечание. Это утверждение верно для многочленов от любого члена переменных над любым полем.
Теорема
Безу. Пусть
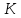 — коммутативное кольцо,
— коммутативное кольцо,
 ,
,
 ,
тогда
,
тогда
 делит
делит
 в том и только в том случае, когда
в том и только в том случае, когда
 в
в
 .
.
Доказательство.
Необходимость
очевидна (если
 в
в
 ,
то есть
,
то есть
 ,
то есть
,
то есть
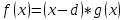 ,
то есть
,
то есть
 ).
).
Для
доказательства достаточности отметим,
что для любого
 :
:


Действительно,
 при делении на
при делении на
 даёт в остатке 0, а в частном
даёт в остатке 0, а в частном
 .
Тогда, очевидно,
.
Тогда, очевидно,
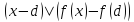 для
для
 ,
если же
,
если же
 ,
то
,
то
 .
Теорема доказана.
.
Теорема доказана.
17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
Если
 — неприводимый многочлен над полем
— неприводимый многочлен над полем
 ,
то кольцо классов вычетов кольца
,
то кольцо классов вычетов кольца
 по модулю
по модулю
 является кольцом без делителей нуля
(это следует из последней теоремы 12-го
вопроса). Однако справедливо более
сильное утверждение.
является кольцом без делителей нуля
(это следует из последней теоремы 12-го
вопроса). Однако справедливо более
сильное утверждение.
Теорема.
Кольцо классов вычетов
 по модулю неприводимого многочлена
по модулю неприводимого многочлена
 есть поле.
есть поле.
Доказательство.
Пусть
 — любой представитель любого класса
вычетов (не совпадающего с
— любой представитель любого класса
вычетов (не совпадающего с
 ).
Так как
).
Так как
 — неприводимый многочлен, то многочлены
— неприводимый многочлен, то многочлены
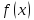 и
и
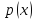 — взаимно просты, следовательно их
— взаимно просты, следовательно их
 .
А тогда, так как
.
А тогда, так как
 — евклидово кольцо, то в нём найдутся
многочлены
— евклидово кольцо, то в нём найдутся
многочлены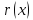 и
и
 такие, что
такие, что
 ,
отсюда ясно, что
,
отсюда ясно, что
 (так как разность
(так как разность
 ,
то есть кратна
,
то есть кратна
 ).
Поэтому
).
Поэтому
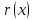 принадлежит классу, обратному к классу,
содержащему
принадлежит классу, обратному к классу,
содержащему
 ,
то есть
,
то есть
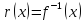 .
Таким образом, все классы, кроме нулевого,
обратимы, то есть
.
Таким образом, все классы, кроме нулевого,
обратимы, то есть
 — поле. Теорема доказана.
— поле. Теорема доказана.
Ясно,
что поле
 над полем
над полем
 является подполем поля
является подполем поля
 .
В этом случае поле
.
В этом случае поле
 называется расширением (или надполем)
поля
называется расширением (или надполем)
поля
 .
.
Элементы
поля
 можно представить в виде многочленов,
степени которых меньше, чем
можно представить в виде многочленов,
степени которых меньше, чем
 (представителей соответствующих классов
вычетов).
(представителей соответствующих классов
вычетов).
Сложение
таких многочленов осуществляется как
обычно, а после умножения надо переходить
к остатку от деления на
 ,
то есть от любого многочлена можно
отнять кратное
,
то есть от любого многочлена можно
отнять кратное
 .
.
На
практике используют замену степеней
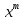 (если
(если
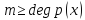 )
линейными комбинациями меньших степеней
)
линейными комбинациями меньших степеней
 .
Действительно, пусть:
.
Действительно, пусть:

Тогда

и далее:

Таким
образом
 выражен через степени не выше
выражен через степени не выше
 ,
то есть не выше степени
,
то есть не выше степени
 .
.
Пример.
Пусть поле
 .
Очевидно, что в
.
Очевидно, что в
 многочлен
многочлен
 — неприводим. Возьмём элемент этого
поля
— неприводим. Возьмём элемент этого
поля
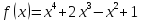 и сравним его по модулю с
и сравним его по модулю с
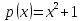 .
.

Тогда

 .
.
Заметим
ещё, что любое расширение
 поля
поля
 можно рассматривать как векторное
пространство над
можно рассматривать как векторное
пространство над
 .
Если
.
Если
 образовано, как в теореме 1 (текущего
вопроса), то базис этого векторного
пространства состоит из многочленов
(точнее, классов, которым принадлежат
эти многочлены):
образовано, как в теореме 1 (текущего
вопроса), то базис этого векторного
пространства состоит из многочленов
(точнее, классов, которым принадлежат
эти многочлены):
 ,
где
,
где
 .
Размерность этого пространства называют
степенью расширения
.
Размерность этого пространства называют
степенью расширения
 над
над
 и обозначают
и обозначают
 .
.
 — степень расширения
— степень расширения
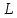 над
над
 .
Обозначение:
.
Обозначение:
 .
.
Пример.
 .
.
Теорема.
Любое конечное поле
 — надполе поля
— надполе поля
 характеристики
характеристики
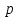 состоит из
состоит из
 элементов, где
элементов, где
 — степень расширения.
— степень расширения.
Доказательство.
Пусть
 .
Это значит, что векторное пространство
.
Это значит, что векторное пространство
 над полем
над полем
 имеет базис из
имеет базис из
 элементов:
элементов:
 .
Но тогда всякий элемент
.
Но тогда всякий элемент
 однозначно представим в виде линейной
комбинации базисных элементов:
однозначно представим в виде линейной
комбинации базисных элементов:
 ,
причём каждый коэффициент
,
причём каждый коэффициент
 ,
может принимать
,
может принимать
 различных значений. Отсюда следует, что
число таких линейных комбинаций равно
различных значений. Отсюда следует, что
число таких линейных комбинаций равно
 .
Теорема доказана.
.
Теорема доказана.
