
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры
- •Литература
|
Экзаменационные вопросы |
© Kovalenko Leonid |
|
по дискретной математике |
|
|
Весь материал взят с книг и научных работ. Ничего не придумано☺ |
|
0. |
Введение. Граф................................................................................................................ |
2 |
1. |
Сеть. Потоки в сети. Теорема Форда — Фалкерсона................................................ |
12 |
2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность,
биективность. Примеры........................................................................................................ |
16 |
3. Бинарное отношение. Свойства. Матрица смежности и граф отношения.
Отношение эквивалентности. Примеры............................................................................. |
24 |
4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры...................... |
30 |
5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа.
Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп |
||||||
Нейтральный элемент. Обратная подстановка. Число |
|
|
|
|
36 |
|
................................................................................................................................................. |
|
|
|
|
|
|
6. |
Группа подстановок. Симметрическая группа |
|
. Умножение |
подстановок. |
||
|
|
элементов группы |
................ |
40 |
||
.................................................................................................................................................7. |
|
|
|
|
|
|
Цикл. Теорема о представлении подстановки в виде произведения независимых |
||||||
циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа |
41 |
|||||
|
|
|
|
|
|
|
8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. |
|||||||||||||||||||||||
идеалах в кольце |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 |
||||
Примеры. Подкольцо. Единица кольца. Поле. Примеры.................................................. |
|
|
|
|
|
|
|
|
|
||||||||||||||
9. Идеал. Главный идеал. Теорема об идеалах поля (только |
|
и ). Следствие об |
|||||||||||||||||||||
|
|
|
|
Классы.................................................................................................................вычетовпомодулю |
|
(поидеалу |
|
|
|
|
|
|
|
|
49 |
||||||||
|
|
|
|
|
|
).Свойства.Малаятеорема |
|||||||||||||||||
10.Сравнения. |
|
|
|
|
теория чисел) ............................................... |
|
|
|
|
|
|
|
|
|
50 |
||||||||
Ферма. Функция Эйлера. Теорема Эйлера ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
11. |
Характеристика кольца. Теорема о характеристике кольца без делителей 0. |
||||||||||||||||||||||
— простой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры. Кольцо классов вычетов. Примеры................................................................... |
|
|
|
|
|
|
|
|
|
|
|
54 |
|||||||||||
12. |
Простой идеал. Необходимое и достаточное условие того, что идеал кольца |
|
|||||||||||||||||||||
|
.............................................................................................................................. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
55 |
|
13. |
Поле классов вычетов. Минимальное поле. Примеры............................................ |
|
|
|
|
|
|
|
55 |
||||||||||||||
16. |
Приводимые и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
56 |
|||||||
14. |
Евклидово кольцо. Свойства (8 свойств). Примеры................................................ |
|
|
|
|
|
|
|
|
|
|||||||||||||
15. Кольцо многочленов |
|
. Условия того, что кольцо |
|
|
|
— евклидово кольцо.... |
58 |
||||||||||||||||
17. |
|
|
|
|
|
неприводимые многочлены в кольце |
|
|
. Примеры. Теорема о |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
разложении |
|
в |
|
на произведение неприводимых |
множителей. Теорема Безу |
...... |
59 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
/ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расширение поля (надполе). Теорема о том, что кольцо классов вычетов |
|
|
||||||||||||||||||||
|
по модулю неприводимого многочлена есть поле. Степень расширения. |
Число |
|||||||||||||||||||||
|
|
= |
|||||||||||||||||||||
элементов этого поля |
............................................................................................................ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
||||||
18. |
Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и |
||||||||||||||||||||||
умножения.............................................................................................................................. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62 |
||
Литература......................................................................................................................... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|||
0. Введение. Граф Граф (в широком смысле) — конечный набор объектов любой природы, которые
называются вершинами, некоторые пары из которых могут быть соединены. |
|||||||||
|
|
|
|
|
|
|
( , ) |
|
|
Граф — множество вершин |
|
и набор неупорядоченных и упорядоченных пар |
|||||||
вершин, где — |
|
, |
|
— |
|
. Обозначается |
|
. Неупорядоченная пара |
|
вершин называется ребром, упорядоченная пара — дугой.
Смежные (соседние) вершины — две вершины, которые соединены ребром.
Смежные (соседние) рёбра (дуги) — два ребра (две дуги), у которых есть общая вершина.
Кратные рёбра (дуги) — рёбра (дуги), соединяющие одну и ту же пару вершин. |
||||||||||||
Петля — ребро, которое начинается и кончается в одной и той же вершине. |
||||||||||||
|
и |
|
1 |
, 2 |
|
|
1 = ( 1, 2) |
только в отношении ребра (дуги) и |
||||
Инцидентность — понятие, используемое |
|
|||||||||||
вершины |
или1 |
два |
|
1 |
|
|
2 |
|
1 |
|
||
вершины:если |
|
|
— вершины,а |
|
|
— соединяющееихребро(дуга), тогда |
||||||
вершина |
|
|
ребро |
|
инцидентны, вершина |
|
|
и ребро |
|
тоже инцидентны. Две |
||
|
|
|
|
ребра (дуги) инцидентными быть не могут. Понятие инцидентности |
||||||||
для орграфов сохраняется (то есть начальная или конечная вершина — не имеет значение), но различается в особых случаях — положительная инцидентность (дуга исходит из вершины) и отрицательная инцидентность (дуга заходит в вершину).
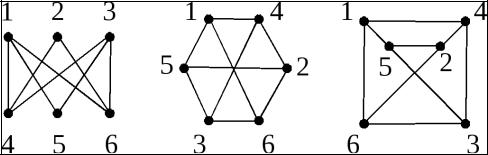
Изоморфизм двух графов — понятие, используемое в случае, если существует перестановка вершин, при которой два графа совпадают. Иначе говоря, два графа называются изоморфными, если существует взаимно-однозначное соответствие между ихвершинамиирёбрами,котороесохраняетсмежностьиинцидентность(тоестьграфы отличаются только названиями своих вершин). В случае матрицы смежности: графы являются изоморфными, если путём перестановки строк и столбцов матрицы смежности первого графа удаётся получить матрицу смежности второго графа.
|
|
|
Рисунок 1. Все три графа — изоморфны |
|
Порядок графа — число вершин в графе: . |
|
|||
считают |
|
|
|
|
Размер графа — число рёбер (дуг) в графе|: | . |
|
|||
Степень |
|
вершины — количество инцидентных| | |
ей рёбер (при этом петли |
|
дважды).
Изолированная вершина — вершина, которая не является концом ни одного ребра.
Висячая вершина (или лист) — вершина, которая является концом ровно одного ребра.
Путь — конечная последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром или дугой. Длина пути — число составляющих его рёбер и дуг.
Простой путь — путь, в котором рёбра (дуги) не повторяются. Элементарный путь — простой путь, в котором вершины не повторяются.
Цикл — путь, в котором первая и последняя вершины совпадают. Длина цикла — число составляющих его рёбер и дуг.
Простой цикл (или контур) — цикл, в котором только первая и последняя вершины совпадают, а все остальные — нет.
Цепь (или маршрут) — путь без повторяющихся рёбер.
Простая цепь (или простой маршрут) — цепь без повторяющихся вершин.
Расстояние между вершинами — минимальная длина пути, который соединяет эти вершины.
Связность означает наличие пути между любой парой вершин.
Бинарное отношение на множестве вершин графа, заданное как «существует путь из в », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа.
Если у графа ровно одна компонента связности, то граф связный.
Компонента связности графа — всякий максимальный связный подграф не орграфа. Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов.
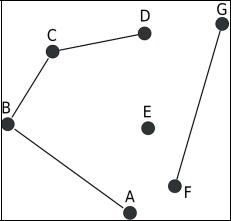
Рисунок 2. Граф с тремя компонентами связности { , , }
Мост (перешеек) — ребро графа, удаление которого увеличивает число компонент связности. (На рисунке выше все рёбра — мосты.)
Гамильтонов маршрут — простой маршрут в графе, содержащий все вершины графа ровно по одному разу.
Гамильтонов цикл — простой цикл в графе, содержащий все вершины графа ровно
по одному разу (кроме первой, естественно). |
|
|
1 − 2 − 3 − 4 − 2 − 5 − |
||
6 − 1 — |
1 − 2 − 3 − 4 − 7 −15− 21−−52−−65− 1 |
|
|||
На следующем рисунке последовательности вершин: |
− 2 − 3 − 4 − 2 − 5 |
— |
|||
маршрут, |
и |
— простые пути1, |
|
||
цикл (но не контур), |
|
— простой цикл (контур). |
|
||
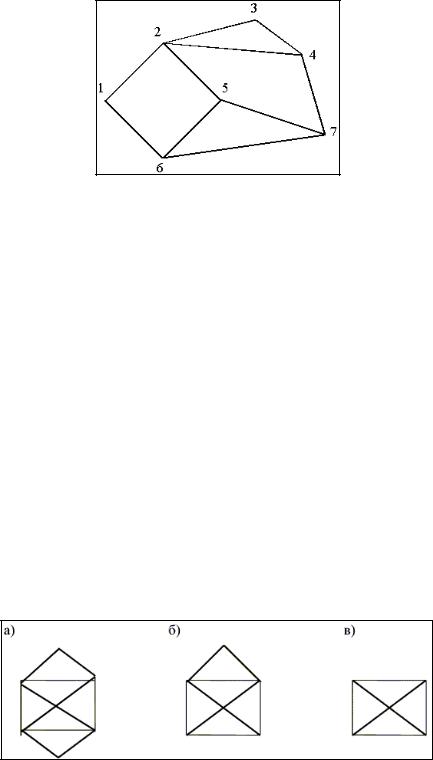
Рисунок 3
Виды графов Пустой граф — граф, в котором есть только вершины (нет рёбер и дуг).
Неориентированный граф (не орграф) — граф, содержащий только рёбра. Ориентированный граф (орграф) — граф, содержащий только дуги. Смешанный граф — граф, содержащий рёбра и дуги.
Ориентированный и неориентированный графы являются частными случаями смешанного.
Гамильтонов граф — граф, в котором есть гамильтонов цикл. (Далее подробнее.)
Полугамильтонов граф — граф, в котором есть гамильтонов маршрут (Далее подробнее.)
Эйлеровграф — граф, в котором существует цикл без повторения рёбер (такойцикл называют эйлеровым), обходящий все вершины графа. (Далее подробнее.)
Полуэйлеров граф — граф, в котором существует маршрут (эйлеров путь), обходящий все рёбра графа ровно один раз. (Далее подробнее.)
Существуют загадки типа «можно ли нарисовать данную фигуру, не отрывая ручку от бумаги», что и соответствует эйлерову или полуэйлерову графу.
Рисунок 4. а) — эйлеров граф, , б) — полуэйлеров граф, в) — граф, не являющийся ни эйлеровым, ни полуэйлеровым.
Связный граф — граф, в котором для любых двух вершин есть путь из в .
Сильно связный (ориентированно связный) граф — ориентированный граф, в
котором из одной любой вершины в любую другую имеется ориентированный путь.
Ациклический граф — граф без циклов.
Нормированный граф — ориентированный граф без циклов. Простой граф — граф без петель и кратных рёбер (дуг). Мультиграф — граф с кратными рёбрами и без петель. Псевдограф — мультиграф с хотя бы одной петлёй.
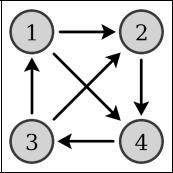
Полный граф — граф, в котором любые две вершины соединены одним ребром.
Турнир — ориентированный граф, в котором каждая пара вершин соединена одной дугой.
Рисунок 5. Турнир
Направленный граф — ориентированный граф, в котором две вершины соединяются не более чем одной дугой.
Дерево — связный граф без циклов. |
|
|
||||||
Лес — множество деревьев. |
1 |
и 2 так, |
что всякое ребро соединяет вершину из |
|||||
с вершиной из . |
|
|||||||
Двудольный |
граф |
— граф, в |
котором |
все вершины можно разбить на два |
||||
1Полный |
|
2 |
|
|
|
|
|
|
непересекающихся подмножества |
|
|
|
|
||||
|
|
двудольный граф — двудольный граф, в котором каждая вершина одного |
||||||
|
|
|
|
|
|
|
|
|
подмножества соединена ребром с каждой вершиной другого подмножества. |
|
|||||||
|
-дольный граф — граф, в котором все вершины можно разбить на |
|
||||||
непересекающихся подмножеств |
|
|
так, что не будет рёбер, соединяющих |
|||||
вершины одного и того же подмножества1, 2, …., |
|
|
||||||
Планарный граф — граф, который можно изобразить диаграммой на плоскости без пересечений рёбер.
Взвешенный граф — граф, в котором каждому ребру поставлено в соответствие некоторое число, называемое весом ребра.
-регулярный граф — граф, в котором степени всех вершин равны .
ВНИМАНИЕ! К сожалению, некоторые из этих терминов не вполне устоялись, так как нет чётких стандартов. В большинстве случаев терминология определяется во вводной части большинства книг по теории графов.
Например, некоторые авторы разрешают мультиграфам иметь петли, а некоторые не разрешают; определения пути и маршрута разнятся…
Основная информация
Лемма 1. Если степени всех вершин в графе больше или равны двум, то граф обязательно содержит контур.
Доказательство. Действительно, выйдя из некоторой вершины и войдя в другую, всегда можно выйти из неё по другому ребру, так как степень каждой вершины больше или равна двум. Выйти из вершины по новому ребру невозможно только в том случае, если эта вершина уже встречалась, а это означает, что можно выделить контур из вершин этого графа.
Теорема (Эйлер). Для того, чтобы данный связный неориентированный граф (возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были чётными. Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечётными, а степени остальных вершин — чётными.
Доказательство этой теоремы начнём с так называемой леммы о рукопожатиях.
Название этой леммы связано с тем, что эта лемма отвечает на следующий вопрос: «У вас собрались гости. Некоторые из них здороваются друг с другом посредством рукопожатий. Какими свойствами обладает число таких людей?» Ответ даётся следующей достаточно простой леммой.
Лемма о рукопожатиях (для неориентированного графа). Сумма степеней всех вершин графа — чётное число, равноеdegудвоенному= 2 | числу( )| рёбер:
( )
Доказательство. Возьмём пустой граф (есть вершины, но нет рёбер). Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любыедвевершины,суммастепенейвсехвершинувеличиваетсяна2 (уоднойвершины добавилась 1, у второй добавилась 1, в итоге 2, остальные по нулям). Продолжая добавления рёбер, на любом шаге получим, что сумма всех степеней вершин чётна и равна удвоенному числу рёбер (добавление ребра увеличивает сумму степеней всех вершин на 2, удаление ребра — уменьшает на 2). Лемма доказана.
Лемма о рукопожатиях (для ориентированного графа). Сумма входящих и
исходящих степеней всех вершин ориентированного графа — чётное число, равное
удвоенному числу дуг: ( ) deg− + ( ) deg+ = 2 | ( )|
Доказательство аналогично доказательству леммы о рукопожатиях в неориентированном графе. Возьмём пустой граф и будем добавлять в него дуги. При этом каждое добавление дуги увеличивает на единицу сумму входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу дуг.
С точки зрения задачи о рукопожатиях это означает, что число гостей, которые поздоровались за руку нечётное число раз, должно быть чётным.
Перейдём к доказательству теоремы Эйлера.
А) Необходимость. Пусть граф является эйлеровым. Тогда в нем имеется эйлеров цикл. Двигаясь по циклу, будем подсчитывать степени вершин. Так как все рёбра в цикле различны, прохождение каждой вершины добавляет 2 в степень этой вершины (то есть каждый «заход» в вершину и «выход» из неё даёт 2 степени вершины). Так как в циклвходятвсерёбра,то,когдаобходбудетзакончен,будутопределеныстепенивсех вершин, которые будут чётными. Таким образом, сумма степеней= 1 всех вершин чётна.
Б) Достаточность. Индукция по числу вершин . При связный граф имеет одну вершину, степень которой чётна, а в таком графе есть эйлеров цикл. В случае, когда в связном графе всего 2 вершины и обе они имеют чётную степень (в этом случае
имеем мультиграф, один из которых изображён на следующем рисунке), ясно, что в этом случае имеется эйлеров цикл (при любой чётной степени этих двух вершин).
Рисунок 6. Мультиграф
в которых строго меньше , и докажем его для графа, имеющего вершин.
Предположим, что наше утверждение верно для всех связных графов, число вершин
По лемме1 в этом графе естьконтур (степеньвсех вершинбольше или равна 2). Если он содержит все рёбра графа, то эйлеров цикл найден (!). Если же этот контур содержит не все рёбра, то удалим все его рёбра из графа. Получим новый граф. Новый граф распадается на компоненты связности, каждая из которых должна иметь общую
вершину с удалённым контуром (иначе первоначальный граф не был бы связным), причём степени всех вершин каждой компоненты чётны и число вершин в ней строго меньше , то есть по индуктивному предположению каждая компонента имеет эйлеров цикл. Теперь мы можем построить эйлеров цикл в данном графе следующим образом. Обходим последовательно рёбра удалённого контура. Далее, если мы пришли в вершину, общую для контура и какой-то компоненты связности, то обходим по эйлерову циклу эту компоненту (то есть присоединяем к контуру этот цикл) и идём по
этому контуру дальше. Тем самым все рёбра будут пройдены, и каждое ровно один раз. |
||
точку и |
|
|
Всё это схематично изображено на следующем рисунке: сначала начинаем обходить |
||
доказано. |
|
, проходим «верхний» граф, затем возвращаемся в |
контур |
; пройдя ребро |
|
далее идём по ребру , обходим «правый» граф и так далее. Утверждение Б
Рисунок 7
В) Необходимость. Пусть граф полуэйлеров. Это значит, что он имеет эйлеров путь, начинающийся в одной вершине и заканчивающийся в другой. Очевидно, что обе эти
вершины должны иметь нечётную степень, а степени остальных чётны.
Г) Достаточность. Пусть граф имеет ровно две вершины нечётной степени и .
Возможны 2 случая( ,: эти) вершины не связаны ребром или связаны. В первом случае, добавляя ребро , получаем граф, все вершины которого чётной степени,
следовательно, он имеет(эйлеров, ) цикл (по предыдущим доказанным утверждениям) и, удаляяизнегоэторебро ,получаемэйлеровпуть.Вовторомслучаеудалимребро. Получим новый граф. Если он имеет 2 компоненты связности, то пройдём одну из них по эйлерову циклу, начиная и заканчивая в вершине, которая в первоначальном графе имела нечётную степень. Затем добавим удалённое ребро (мост), пройдём его — попадём в другую вершину, которая ранее имела нечётную степень, и пройдём вторую компоненту связности по эйлерову циклу. Во всех разобранных случаях получим эйлеров путь, который начался в одной из вершин с нечётной степенью и закончился в другой.
Теорема доказана. |
|
|
|
|
|
Примечание. Если граф (или мультиграф без петель) содержит |
вершин нечётной |
||||
степени, то его можно разбить на |
|
полуэйлеровых графов (то2 есть нарисовать |
|
||
росчерками пера). Доказательство |
аналогично доказательству теоремы Эйлера. |
||||
|
|
|
|
||
Имеется простой алгоритм (так называемый алгоритм Флери) для нахождения эйлерова цикла (конечно, если этот цикл существует), который состоит в следующем: начинаем с любой вершины и «стираем» пройденные ребра (удаляем также изолированные вершины, которые при этом образуются. При этом по мосту (перешейку) проходим только в случае, когда нет других возможностей.
Рисунок 8. Рёбра пронумерованы в порядке их прохождения. Эйлеров цикл: .
Очевидно, что для того, чтобы построить эйлеров путь достаточно использовать алгоритм Флери, который надо начать с вершины, имеющей нечётную степень.
Рассмотрим некоторые приложения теоремы Эйлера, которые в основном связаны с так называемой задачей китайского почтальона.
Пусть имеется некоторый связный граф, рёбрам которого приписаны некоторые числа, называемые весами рёбер. Требуется найти такой цикл, при котором каждое ребро проходится по крайней мере один раз и суммарный вес всех рёбер, вошедших в цикл, минимален. Заметим, что если граф является эйлеровым, то любой эйлеров цикл решает поставленную задачу (для эйлерова графа веса роли не играют).
Эта задача имеет много приложений, например, поливка улиц одной машиной (здесь ребра графа — дороги, а перекрёстки — вершины; веса — это длины дорог), а также сбор мусора, доставка почты или даже наилучший маршрут для осмотра музея или уборка помещений и коридоров в больших учреждениях.
Заметим,чтоимеетсяалгоритмрешениязадачикитайскогопочтальона,ноонтребует достаточно длительного описания.
Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном связном графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут — простым маршрутом), то граф
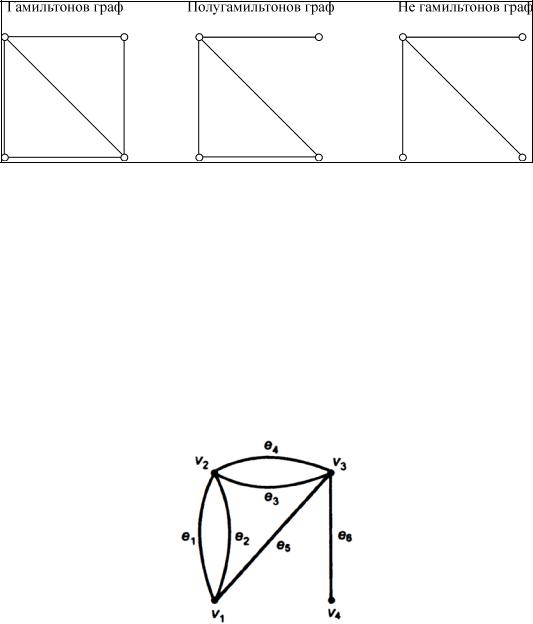
называется гамильтоновым (полугамильтоновым), и соответствующий цикл (маршрут) называют гамильтоновым циклом (маршрутом).
Далее изображены гамильтонов, полугамильтонов и не гамильтонов графы.
Рисунок 9
Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, «хорошего» решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном — это теоремы типа «если в графе достаточное число рёбер, то он гамильтонов». Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, поскольку в графах такого типа вершин может быть очень много,
а рёбер сравнительно мало. |
|
|
|
|
|
Приведём без доказательства самую известную теорему. |
|
||||
Теорема (Дирак, 1952). Если в связном графе с |
≥ 3 |
вершинами степени всех |
|||
вершин больше или равны |
, то граф гамильтонов. |
|
|||
2 |
|
Матрицы |
|
|
|
|
|
|
|
|
|
Рисунок 10. Неориентированный мультиграф
Трудно переоценить роль матриц в теории графов. Перечислим наиболее известные.
Матрица смежности. Это квадратная матрица порядка |
|
( |
|
— число вершин), в |
||||||||
стоит |
|
|
|
|
|
|
петель, а если петли есть в |
|||||
которой нули стоят по главной диагонали (если в графе нет |
|
|
рёбрами, то |
|
. |
|||||||
матрицы |
|
|
|
|
равен 1, |
если эти вершины связаны |
|
|
||||
вершине |
|
(и число этих петель равно ), то на главной диагонали в строчке с номером |
||||||||||
|
число |
|
). Если вершина |
связана с вершиной одним ребром, то элемент |
||||||||
Аналогичным образом |
|
|
|
|
|
|
= |
|
||||
|
смежности |
|
|
|
|
|
|
|
|
|||
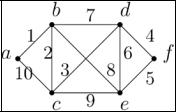
строятся матрицы смежности для орграфов и для мультиграфов. Для предыдущего рисунка матрица смежности такая:
|
|
|
|
|
|
1 |
: |
|
1 |
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
0 |
2 |
1 |
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
0 |
2 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
3 |
: |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
4 |
|
|
1 |
2 |
0 |
|
|
1 |
|
|
|
|
Теорема. Если матрица |
|
|
|
: 0 |
0 |
1 |
|
|
0 |
|
|
|||||||
|
|
|
|
смежности графа с |
|
|
вершинами есть , то элемент |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
матрицы |
|
равен числу маршрутов длины |
|
из вершины с номером |
в вершину с |
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
номером |
(под длиной маршрута понимается число |
рёбер в этом маршруте). |
|
|||||||||||||||
Доказательство |
= 1 |
|
2 |
|
… 3 |
|
1 1 2 … −1 |
|
|
|
||||||||
. По правилу перемножения матриц: |
|
|
|
|||||||||||||||
Для обычного графа каждый=1 |
|
|
=1 |
|
=1 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
элемент матрицы смежности равен или 0, или 1. Значит, |
|||||||||||||
в написанной сумме каждое слагаемое равно или 0, или 1, причём оно равно 1 тогда и только тогда, когда все множители равны 1. Но в этом случае индексы у множителей
указывают некоторый путь из -й вершины в |
-ю, а тогда сумма всех этих единиц равна |
||||||||||||||||||||||
числу маршрутов из |
-й вершины |
в |
|
-ю, |
и |
теорема доказана. |
Для мультиграфов |
||||||||||||||||
доказательство аналогично. |
|
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
равны числу |
маршрутов |
|
длины |
= |
|
|
|
|
|
|
|
|
|
3 |
|||||||||
Замечание. В частности, матрица |
|
|
|
2 составлена из целых чисел , которые |
|||||||||||||||||||
трёх рёбер) из |
|
( ) |
|
|
|
соединяющих вершины |
|
и |
. Аналогично |
из |
|||||||||||||
составлена из чисел |
|
3 |
|
, равных числу маршрутов длины 3 (то |
есть маршрутов |
||||||||||||||||||
— число рёбер графа, при этом её элементы |
|
|
× |
|
|
|
|
|
|||||||||||||||
|
|
вершины |
в вершину |
и так далее. |
|
|
|
|
|
|
|
|
|
||||||||||
Матрица инцидентности |
. Это матрица |
размера |
|
|
, где |
|
— число вершин, а |
|
|
||||||||||||||
инцидентна |
ребру с |
номером |
(если |
|
|
|
равны 1, если вершина с номером |
||||||||||||||||
|
(для ориентированного |
|
|
|
ребро неориентированное), или является |
||||||||||||||||||
начальной |
ребра). |
Заметим, |
что матрица инцидентности |
||||||||||||||||||||
сравнительно редко используется, так как в современных условиях (где число рёбер часто очень велико) она имеет слишком большое число столбцов.
|
|
|
|
|
|
|
1 |
: |
|
|
2 |
|
3 |
|
4 |
|
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Для предыдущего рисунка матрица инцидентности такая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
: |
1 |
1 |
|
0 |
|
0 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
1 |
|
1 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
3 |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Структурная матрица. |
|
4 |
: |
0 |
|
0 |
|
1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
0 0 0 0 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
Именно эта матрица имеет особое значение в теории сетей |
||||||||||||||||||||||||||||||||
связи. Структурная матрица — это символьная матрица порядка |
|
(размера |
|
|
), где |
||||||||||||||||||||||||||||||||||
ребром |
, то элемент |
|
|
|
, |
|
при |
|
= 1 |
|
|
|
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
— число вершин графа, причём её элементы — символьные |
обозначения рёбер. На |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
× |
|
|
|||||||||||||||||||||||||||||
чертой наверху |
: |
|
. = |
|
|
|
|
> |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
главной диагонали стоят 1, то есть |
|
|
|
. |
Если при |
|
|
|
|
|
вершины |
|
и |
|
соединены |
||||||||||||||||||||||||
|
|
|
|
. = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
нет, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
составляться |
и |
для |
орграфа, и для |
||||||||||||||||||||
|
|
= 0 |
|
|
|
|
|
|
|
|
|
|
— отрицание , которое обычно отмечается |
||||||||||||||||||||||||||
|
|
|
|
Если же ребра из вершины с номером |
|
в вершину с номером |
|||||||||||||||||||||||||||||||||
|
|
Структурная |
|
|
матрица |
может |
|
|
|
соединяют |
|
|
вершины, то |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
|
и |
|
|
> |
|
|
|
|
|
|
две |
|
|
|
|
|
||||||||
мультиграфа без петель (здесь если два ребра |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
соответствующий элемент при |
|
|
|
|
равен |
|
|
|
, а при |
|
|
|
|
|
этот элемент равен |
|
|
||||||||||||||||||||||
|
Для предыдущего рисунка структурная матрица такая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
3 |
|
4 |
|
1 |
: |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
5 |
4 |
||||||
|
2 |
: |
1 1 2 |
|
|
3 |
0 |
||||
|
3 |
: |
|
|
5 |
|
|
|
06 |
||
|
|
3 |
1 |
4 |
|||||||
Отметим, что в |
4 |
: |
|
|
|
|
|
|
1 |
|
|
|
|
|
0 |
|
0 |
|
6 |
|
1 |
||
|
|
|
|
|
|
|
|
||||
|
учебных |
целях, |
когда |
действия с |
матрицами осуществляются |
||||||
студентами «вручную» (число вершин в графе невелико), можно обозначать ребра |
||||||||||||||||||||
|
|
|
и с чертой сверху при |
. |
( , ) |
|
|
|
|
|
|
|
||||||||
латинскимибуквамибезиндексов |
|
|
итакдалее, ноприиспользованиикомпьютера |
|||||||||||||||||
<Теорема |
. |
Для |
того чтобы> |
найти |
все простые пути из вершины в вершину |
|||||||||||||||
гораздо удобнее обозначать ребра , , , если это ребро соединяет вершины |
|
|
и |
|
при |
|||||||||||||||
достаточно раскрыть минор |
|
|
структурной матрицы методами булевой |
|
алгебры |
|||||||||||||||
(то есть вычеркнуть из структурной( , ) |
матрицы строчку с номером |
и столбец с номером |
||||||||||||||||||
). При этом раскрытие минора производится обычными действиями |
с определителями, |
|||||||||||||||||||
но |
сложение заменяется дизъюнкцией, умножение — конъюнкцией, знаки умножения |
|||||||||||||||||||
на числа не используются. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
2 |
|
5 |
0 |
|
|
|
|
= 0 0 6 1 2 |
3 5 4 |
|
|
|
|
|
|
|
||
|
|
1 |
3 4 |
0 |
|
|
|
|
|
|
|
|
|
|
||||||
|
Для предыдущего рисунка нахождение всех простых путей из (1) в (4): |
|
|
|
|
|
||||||||||||||
|
3 |
4 |
|
1 |
6 |
|
по3ему столбцу |
|
1 |
|
3 6 2 4 6 |
|
|
5 |
6 |
|||||
|
Подробно |
= 6 |
( 1 |
2)( 3 |
4) 1 5 = 1 3 6 1 |
4 6 2 |
|
|||||||||||||
|
|
|
|
|
доказывать эту теорему не будем, но отметим, что определитель равен |
|||||||||||||||
сумме (в данном случае дизъюнкции) элементов, взятых по одному из каждой строчки и каждого столбца с определенным знаком. В нашем случае знаки не присутствуют, а
значит, любой член раскрытия определителя всей структурной матрицы |
|||||||||||||
соответствует циклу в графе. Если же брать минор |
|
|
, то |
его раскрытие |
|||||||||
раз). Это и означает, что мы получаем маршрут |
от вершины с номером |
к вершине с |
|||||||||||
|
|
|
|
|
|
|
|
элемент |
, нобезсамого |
||||
соответствуеттемчленамопределителя,вкоторыхимелся ( , ) |
|
|
только один |
||||||||||
номером . |
|
|
|
|
|
|
|
|
|
|
|
||
этого элемента (таким образом, |
индексы и встречаются вместо(двух, ) |
||||||||||||
чтобы не проходить по одному |
1 = 1, = = 0 |
|
|
|
|
|
|
||||||
Понятно, что раскрытие минора методами булевой алгебры предусматривает, что |
|||||||||||||
верны следующие соотношения: |
|
|
|
|
|
, (это свойство нужно, для того |
|||||||
использовать правило поглощения, то получим все |
|
= |
|
|
|
|
|||||||
|
|
|
ребру дважды в противоположных направлениях), а |
||||||||||
также используется правило простого поглощения: |
|
|
|
|
. Видно, что если не |
||||||||
|
|
|
|
|
маршруты (без повторения рёбер), |
||||||||
Замечание 2. После получения ответа чёрточки над |
|
( , ) |
|
( , ) |
|
|
|||||||
связывающие вершины и . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание 1. Если граф |
не |
ориентирован, то миноры |
|
|
и |
|
|
совпадают. |
|||||
обозначениями рёбер (то есть отрицания) можно убрать (на самом деле «черта» над ребром означает, что ребро проходится от вершины с большим номером к вершине с меньшим номером). Затем рекомендуется записать каждый путь по порядку прохождения рёбер (в этом случае удобны обозначения рёбер с индексами вершин).
Сечение (разрез) между вершинами и — неизбыточный набор рёбер, при удалении которых из графа теряется связь между данными вершинами (не существует
пути из вершины в вершину ). Слово «неизбыточный» означает, что если любое ребро изсечения снова возвратить в граф, то связь восстановится.Заметим, чтосечений
между данными вершинами может быть много, и они могут содержать разное количество рёбер.
Естественно, что если известны все пути из вершины в вершину , причём эти пути заданы в виде ДНФ, то есть дизъюнктивной нормальной формы (а именно такой вид получается после раскрытия соответствующего минора структурной матрицы), то все сечения между этими вершинами можно получить отрицанием этих путей (по правилу де Моргана конъюнкцию заменить на дизъюнкцию и наоборот), затем полученное выражение снова привести к ДНФ, используя раскрытие скобок по обычным правилам; при этом правило поглощения обеспечит неизбыточность набора рёбер в каждом
сечении. Ясно, что знаки отрицания (чёрточки над символами рёбер) можно опустить.
Для1 3предыдущего6 1 4 6 примера2 3 6 нахождение2 4 6 5 6всех сечений между (1) и (4):
→ ( 1 3 6)( 1 4 6)( 2 3 6)( 2 4 6)( 5 6) = = 1 2 5 3 4 5 6
1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
Сеть — связный граф, в котором заданы «пропускные= 0 способности» рёбер, то есть
. Эти числа неотрицательные, причём тогда и только тогда, когда нет
числа ребра, соединяющего вершины и .
Такимобразом,можносчитать,чтопропускныеспособностирёберзаданыдлялюбой пары вершин. В дискретной математике пропускные способности рёбер, как и все возникающие константы, считаются целыми (или рациональными) числами.
Заметим, что сети имеют огромные приложения, в частности, «сети планирования» (имеется в виду планирование производства некоторых новых, достаточно сложных изделий), где «пропускные способности» рёбер — это время, за которое нужно из нескольких узлов изделия (вершин графа) получить другой (более сложный) узел. Сетевое планирование здесь не исследуется, так как гораздо больший интерес представляет сеть связи, где пропускные способности рёбер — это обычно «количество одновременных разговоров», которые могут происходить между телефонными узлами
(вершинами графа). |
|
|
|
|
|
|
|
из вершины с номером в |
|
|||||||
количество условного «груза», перевозимого |
(то есть |
|||||||||||||||
Поток в сети между |
(источником) |
и |
|
(стоком) |
— набор чисел |
|
||||||||||
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
вершину с |
||
номером ), удовлетворяющих четырём условиям: |
|
|
|
|||||||||||||
• |
Числа |
|
|
, причем если |
|
=, то |
|
|
(нет( , )встречных перевозок). Это |
|||||||
• |
Числа |
|
≥ 0 |
|
(провозимый по ребру груз не должен превосходить пропускной |
|||||||||||
|
|
|
|
|
|
|
> 0 |
|
из= 0 |
|
— насыщенно. |
|
|
|||
|
способности этого ребра). Если |
|
|
, то ребро |
|
|
||||||||||
|
условие |
превращает |
поток |
в |
орграф: |
мы считаем, что в паре вершин, |
||||||||||
|
определяющей ребро, первой является та, |
которой груз отправляется, а второй |
||||||||||||||
— та, куда он отправлен.
•Если вершина — промежуточная (не совпадает с источником и стоком), то
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
То есть количество груза, вывозимого |
из вершины |
|
, равно количеству груза, |
||||||||||
ввозимого в эту вершину. |
|
|
|
|
|
|
|
||||||
• Количество груза, вывозимого из источника , |
должно быть равно количеству |
||||||||||||
груза, ввозимого в сток |
|
: |
= |
= |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Число |
|
— величина данного потока |
(или просто поток между и ). |
сечения |
|||||||||
Пусть |
|
|
|
|
|
|
|
и |
. Тогдавеличиной |
||||
|
имеетсянекотороесечениемеждувершинами |
входящих |
|
|
|||||||||
называется сумма пропускных способностей рёбер, |
в это сечение. |
||||||||||||
Сечение называется минимальным (максимальным), если его величина минимальна (максимальна) по сравнению с величинами всех остальных сечений
между рассматриваемыми вершинами в данной сети. |
|
|
|
|
|
|
Теорема Форда — Фалкерсона (1955). Максимальный поток между вершинами |
и |
|||||
равен величине минимального сечения между этими вершинами. |
|
|||||
Доказательство этой теоремы является конструктивным (то есть показывает, |
как |
|||||
найти нужный максимальный поток). |
|
|
|
|
|
|
1. Докажем сначала, что любой потокмежду вершинами |
|
и |
меньше или равен |
|||
величине любого сечения. Пусть дан некоторый поток и |
некоторое сечение. Величина |
|||||
|
|
|
|
|
|
|
данного потока складывается из величин «грузов», перевозимых по всем возможным путям из вершины в . Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести «груза»
больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна сумме всех пропускных способностей рёбер данного сечения. Утверждение доказано.
Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального
сечения. |
|
нулевой, когда |
все |
|
). |
|
|
(какой-то поток всегда существует, например, |
|
|
|||||
2. Докажем теперь обратное неравенство. |
Пусть имеется некоторый поток |
|
|||||
помечать вершины графа, причём считаем, что все помеченные |
|
= 0 |
|
Будем |
|||
только те |
|
|
вершины образуют |
||||
|
|
|
|||||
множество . Пометки вершин производятся от источника. Далее можно помечать непомеченные вершины, для которых найдётся ненасыщенное ребро из помеченной вершины или даже насыщенное ребро, если оно направлено из непомеченной в помеченную (то есть обратно направлено). Каждая пометка вершины (если+ эта вершина− может быть помечена) состоит из двух чисел: первое число — это « » или « » номер вершины (из ), с которой смежна новая помечаемая вершина, и второе — (обязательно должно быть положительным) — это фактически та добавка к
потоку, которая может быть «довезена» в эту вершину из источника по сравнению с |
|||
Более точно, |
|
|
образуется следующим образом: |
исходным потоком |
|
, допускаемая пропускной способностью ребра. |
|
множество помеченных вершин

• Источник принадлежит и его пометка всегда имеет вид (0, ∞); второе число, условно говоря, равно бесконечности — что для дискретной математики означает, что это больше любого реального числа, которое нам встретится.
|
|
|
|
|
|
|
|
|
|
|
|
|
< |
|
|
|
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
• |
то вершина также |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
*. Заметим, |
что |
|
здесь |
|
число |
|
|
|
— это |
число |
+ , |
|
|
|
= |
|||||||||||||||||||||||||||
|
Если вершина |
|
принадлежит |
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
(дуга |
|
|
|
|
|
— прямая и ненасыщенная), |
|||||||||||||||||||||||||
|
min{ , |
− } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
принадлежит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
равна |
|
|
|
|
, где |
|
|
||||||||||||||||||||||
|
( , ) является |
|
|
|
|
|
|
|
|
и пометка вершины |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уже помеченной |
||||||||||||||
|
вершины |
|
, а знак « » перед номером |
|
означает, что дуга, связывающая вершины |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
прямой и ненасыщенной (идёт от |
|
к |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
• |
номером |
|
|
также |
должна |
|
|
|
|
|
|
|
> 0 |
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
что уже |
|
помеченная вершина |
|
|
|
смежна с |
|
|
|
|
|
|
|
|
− , |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
Если вершина |
|
принадлежит |
|
|
|
|
и |
|
|
|
|
|
|
|
|
(дуга |
|
|
|
|
|
— обратная), то вершина с |
|||||||||||||||||||||||||||
|
min{ , |
|
+ |
|
} |
|
|
принадлежать |
|
|
и её пометка |
|
|
|
|
, где « |
|
» означает, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
* — вместо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
непомеченной обратной дугой, |
|
|
|||||||||||||||||||||||
всех |
|
будет |
= min{ , − |
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
− |
|
|
отрицательным). = |
||||||||||||||||||||||
** — вместо |
|
|
|
|
|
** (груз, направляемый |
|
в вершину |
|
, считаем |
||||||||||||||||||||||||||||||||||||||||
= min{ |
, + } |
можно написать |
|
= + |
, так как минимум от |
|||||||||||||||||||||||||||||||||||||||||||||
всех |
|
будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
рассматриваться далее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
рассматриваться далее. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Таким образом, построение множества |
|
|
|
является индуктивным, то естьновая вершина |
||||||||||||||||||||||||||||||||||||||||||||||
добавляется в , если она смежна с |
|
некоторой вершиной, уже входящей в |
|
|
, |
и связана |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
с ней либо прямой |
|
дугой, либо обратной дугой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Послетого, какпостроениемножества |
|
закончено(кнемунельзядобавитьновых |
||||||||||||||||||||||||||||||||||||||||||||||||
вершин), возможны 2 случая. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1. Сток (то есть вершина с номером |
|
) не входит в множество вершин |
|
. Тогда |
||||||||||||||||||||||||||||||||||||||||||||||
обозначиммножествовершин,не |
входящихв , через |
|
|
. Нашграфпоусловиюявляется |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ребра. По правилам построения |
|
|
|
|
|||||||||||||||||||||||||||||||||
связным, поэтому из |
в |
идут некоторые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
также, что сумма пропускных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ребра являются прямыми |
насыщенными дугами. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Ребра, идущие из множества |
в |
|
|
|
|
, образуют сечение между вершинами |
|
|
и |
|
. Видно |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
способностей рёбер этого сечения (а все эти ребра |
|||||||||||||||||||||||||||||||||||||||
являются прямыми, насыщенными) равна потоку из |
|
|
в |
|
|
. Значит, данный поток |
||||||||||||||||||||||||||||||||||||||||||||
является максимальным (так как он равен величине некоторого |
сечения), |
|
а данное |
|||||||||||||||||||||||||||||||||||||||||||||||
сечение является минимальным.
|
Рисунок 11 |
|
второе число её пометки с> 0 . Тогда, очевидно, что между вершинами |
и |
|
2. Сток (то есть вершина номером ) входит в множество вершин |
, и пусть |
|

и найдём минимум |
|
из символов, являющихся вторыми числами { , 1, 2, … , , } |
|||||||||||
существует путь (состоящий из направленных рёбер — прямых и обратных дуг), |
|||||||||||||
соединяющий эти вершины. Обозначим вершины этого пути через |
|
||||||||||||
Ясно, что вдоль |
|
|
= min{∞, 1, 2 |
, … , , } |
|
|
меток вершин вдоль |
||||||
этого пути: |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
рассматриваемого пути поток можно увеличить на |
(с учетом знака |
||||||||||
первогочисламетки,тоестьприбавляяегокужеимеющемусяпотоку |
наребрев случае |
||||||||||||
знака « » и вычитая в случае знака « |
|
»; при этом для некоторых рёбер может |
|||||||||||
обратная |
|
|
|
≤ |
+ |
|
|
|
|
|
|||
получиться отрицательное число, но оно обязательно будет |
по абсолютной величине |
||||||||||||
меньше+ |
, так как по построению |
|
− |
|
|
для всех |
|
и , а это означает, что |
|||||
дуга должна поменять направление, то есть она становится прямой дугой и её |
|||||||||||||
нагрузка будет равна модулю числа − ≤ |
). |
|
|
|
|
||||||||
Схематичный пример маршрута представлен на следующем рисунке.
Рисунок 12
Заметим, что дуга, выходящая из источника, и дуга, входящая в сток, должны быть
обязательно прямыми. |
|
|
|
) и вычитая это из |
|
для обратных дуг, получим |
||||||
число будет |
|
к |
|
|
|
|
|
|
||||
Прибавляя |
|
|
для прямых дуг этой цепи (по построению видно, что полученное |
|||||||||
новый поток из вершины в |
|
|
|
|
|
|
|
|
||||
меньше или равно |
|
|
|
|
|
|
||||||
|
|
|
|
|
вершину (легко проверить простым рассуждением, что |
|||||||
дляновыхчиселвыполняются |
все4условия |
определенияпотока). Крометого,величина |
||||||||||
нового потока по сравнению со старым увеличилась на |
> 0 |
. Для нового потока снова |
||||||||||
проведём ту же процедуру и так далее. |
|
|
||||||||||
Так как каждый раз величина потока увеличивается, по крайней мере, на 1 (пропускные способности рёбер являются целыми (рациональными) числами), а величина максимального потока ограничена (величиной минимального сечения), то эта процедура не может продолжаться бесконечно и, значит, на каком-то шаге получим поток, для которого вершина не входит в , то есть поток является максимальным и величина его равна величине минимального сечения. Теорема доказана.
Рассуждение теоремы Форда — Фалкерсона фактически является алгоритмом нахождения максимального потока между двумя вершинами (или доказательством того, что этот поток является максимальным).
Примечание. Если в данной сети имеется несколько источников и несколько стоков, то описанный выше алгоритм можно применить следующим образом. Вводим новый источник и новый сток, причём новый источник соединяем рёбрами со всеми источниками, а новый сток — со всеми стоками, при этом пропускные способности новых рёбер считаем сколь угодно большими числами, так что эти дуги в любом возможном потоке были бы ненасыщенными (напомним, что ребра, идущие из источника и ребра, идущие в сток, всегда являются прямыми дугами). После этого для нового графа решаем задачу о максимальном потоке (из одного нового источника в один новый сток). Решив её, стираем все введённые ребра и вершины.
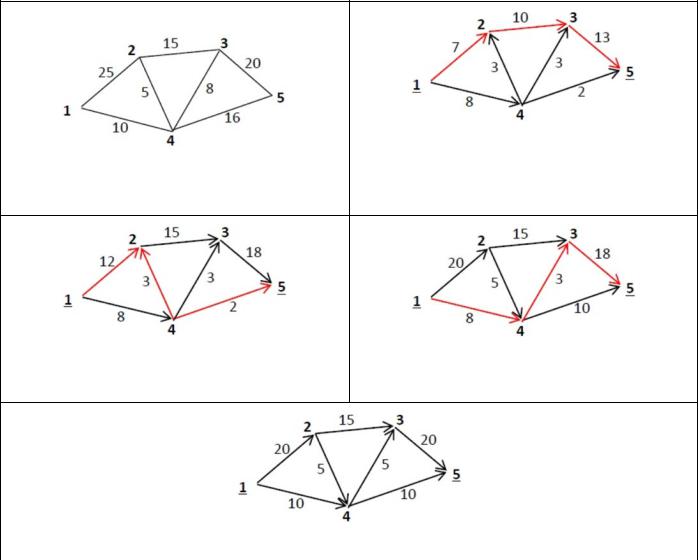
Пример.
Таблица 1
Сеть |
= 7 + 8 = 13 + 2 = 15 |
|
Исходный поток |
|
= min(25 − 7,15 − 10,20 − 13) = 5 |
= 12 + 8 = 18 |
+ 2 = 20 |
= 20 + 8 = 18 + 10 = 28 |
= min(25 − 12,5 + |
3,16 − 2) = 8 |
= min(10 − 8,8 − 3,20 − 18) = 2 |
|
Дуги |
12.→ 4,2 → 4,2 → 3 |
— насыщенные и образуют сечение, значит |
|
= 30 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
Функция. Бинарное отношение. Тотальность, сюръективность, |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
инъективность, биективность. Примеры |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
называются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
— совокупность |
объектов |
|
любой |
|
природы. Эти |
объекты |
||||||||||||||||||||||||||||||||||||
|
Множество |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
элементами множества. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
(или |
|
|
|
|
|
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
означает, |
|
элемент |
|
||||||||||||||
|
Символ |
|
|
— отношение принадлежности. Запись |
|
|
|
|
что |
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. Если элемент |
|
|
не принадлежит множеству , |
то пишут |
|||||||||||||||||||||||||||||||
принадлежит множеству |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
Принцип |
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
. Но |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||
же элементов. Пример: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{2,4,6} = {4,2,6} = |
{2,4,4,6} |
|
{1,2} ≠ {1,2} |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
объёмности. |
|
|
|
|
|
означает, что множества |
|
и |
|
состоят из одних и тех |
|||||||||||||||||||||||||||||||
|
Символ |
|
|
|
отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
означает, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
≠ |
|
|
|
|
|
|
|
|||||||||
множества |
|
есть элемент множества |
|
. То есть |
|
— подмножество множества . |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Символ |
|
|
|
|
— |
|
|
|
|
|
|
|
|
строгого включения (то |
есть |
|
|
). Запись |
|
|
||||||||||||||||||||||||||
|
Заметим, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
есть элемент множества |
|
и |
|
|
|
|
по |
||||||||||||||||||||||
|
|
|
|
что каждый элемент множества |
|
|
|
|
больше |
||||||||||||||||||||||||||||||||||||||
количеству элементов. То есть |
|
— |
собственное подмножество множества . |
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
• |
|
|
|
, то |
|
. |
|
|
|
|
|
|
Если |
, |
, то |
. |
|
|
|
|
|
||||
• |
|
|
. |
|
|
= |
|
|
|
|
|
|
Нельзя , |
|
|
|
|
|
|||||||
• |
Если |
|
|
|
|
|
|
|
|
|
1 {1} |
{1} |
|
, но неверно, что |
|
, а |
1 {1} |
— верно. |
|
||||||
{1Пустое} |
множество1 —{1} |
|
|
|
|
, |
||||||
|
|
|
смешивать понятия принадлежности и включения. Хотя |
|
||||||||
|
|
|
|
|
|
множество, не содержащее элементов. Пустое множество |
||||||
есть подмножество |
любого множества. |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
У |
каждого множества |
есть два |
подмножества, |
которые называют |
||||||||
несобственными — само множество и пустое множество. Все остальные
подмножества — собственные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множеством-степенью (или булеаном) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и обозначается |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
называется |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Множество всех подмножеств |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
= |
|
{1,2,3}, ( ) |
|
= |
, |
{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. |
|
|
|
{1}, {2}, {3}, {1,2}, {1,3}, {2,3} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, {1,2,3} |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
. Собственные |
||||||||||||||||||||||||||
элементов. |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, несобственные: |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
подмножества |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Если множество |
|
|
|
|
состоит из |
|
|
|
элементов, |
|
|
то множество |
|
состоит из |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
элементами множества |
|
или |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
… |
|
= |
|
|
|
|
|
|
. |
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Объединение множеств ( |
|
|
|
|
|
|
) |
— множество, |
все элементы которого являются |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. |
= |
{1,3,5}, = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
{ |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
} |
|
1 |
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
{4,5,6}, = |
{1,3,4,5,6} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
элементами множеств |
|
и |
|
: |
∩ |
|
= |
|
|
|
|
|
|
|
|
|
|
. |
|
∩… ∩ = |
|
|
|
|
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
∩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Пересечение множеств |
|
|
|
|
|
|
) |
— множество, |
все элементы которого являются |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Очевидно, что |
∩ |
|
и{ |
|
| |
|
|
|
|
|
. |
|
|
|
|
|
} |
. |
1 |
|
|
|
|
|
|
|
|
=1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
Пример. |
|
|
|
|
|
|
∩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
Множества= |
{1,3,5}, = |
{4,5,6}, ∩ = |
{5} |
|
|
|
|
∩ = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Разность ( |
|
|
|
|
) — множество, |
|
|
все |
|
|
|
|
|
|
|
|
|
|
|
}. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
Пример. |
и не |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
{ | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
— непересекающиеся, если |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
= {1,3,5}, = {4,5,6}, |
|
|
|
|
|
элементы |
которого |
|
являются |
элементами |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
множества |
= {1,3}, |
|
|
= |
{4,6} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
принадлежат множеству |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
либо в |
|
, либо в |
|
|
|
но не в обоих. |
|
|
|
|
|
{ | |
|
|
} |
= |
( ) |
( ) |
. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Симметрическая разность ( |
|
|
|
|
|
|
) |
— множество, |
|
каждый элемент которого есть |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример |
|
= |
{1,3,5}, = |
{4,5,6}, |
|
= |
{1,3,4,6} |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Универсальное множество — множество всех рассматриваемых в ходе данного |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Пример. |
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||||||
рассуждения множеств. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
= ∩ |
|
|
|
|
|
|
|
, которыенепринадлежатмножеству |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Дополнение( |
|
|
) — множествовсехэлементов |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
. То есть |
|
= |
{1,3,5}, = |
{4,5,6}, |
|
= |
{1,2,3,4,5,6}, |
|
= |
{2,4,6}, |
= {1,2,3} |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. Причём: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
̅ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
× = |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
Прямое (декартово) произведение ( |
|
|
|
|
|
|
|
— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
{( , )| |
|
, |
|
} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множество всех упорядоченных пар, |
||||||||||||||||||||||||||||||||||||
где первый элемент |
|
принадлежит |
множеству |
|
|
|
|
, |
а |
второй |
множеству |
|
|
: |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||

упорядоченных наборов из |
|
элементов |
|
× … × , где |
1 |
1, … , |
. |
То есть |
||||||||||||||||
|
Прямое произведение |
|
|
|
|
|
( 1 |
, … , Каждый) |
|
|
|
|||||||||||||
|
|
множеств ( |
} |
|
) — множество всевозможных |
|||||||||||||||||||
1 |
× … × = |
{( 1, … , )| 1 |
|
1, … , |
|
|
такой |
набор элементов |
||||||||||||||||
множества и обозначается 2 |
= × . Аналогично -ая степень : = × … × . |
|
||||||||||||||||||||||
называется кортежем. Произведение множества самого на себя называется квадратом |
||||||||||||||||||||||||
|
Пример. |
|
|
|
{ , , }, |
× = {(3, ), (3, ), (3, ), (8, |
|
. |
|
|||||||||||||||
|
|
Пример. = {3,8}, = |
), (8, ), (8, |
)} . |
|
|||||||||||||||||||
( |
Операция = |
|
{0,1}, × × = {(0,0,0), (0,0,1), |
(0,1,0), (0,1,1), |
(1,0,0), (1,0,1), (1,1,0), (1,1,1)} |
|
||||||||||||||||||
|
× |
) и не |
|
|
|
|
|
× |
( ? ) = ( × ) |
? ( × ) |
|
|
|
|
|
|||||||||
|
× ≠ × |
|
|
|
|
|
|
|
|
× ( × ) ≠ ( × ) × |
|
), |
но не коммутативна |
|||||||||||
|
|
|
дистрибутивна ( |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
ассоциативна ( |
|
|
|
|
|
|
|
|
). |
|
|
|
|
||||||
|
Диаграммы Эйлера — Венна. |
На диаграммах Эйлера — Венна множество |
|
|||||||||||||||||||||
изображается |
|
прямоугольником, |
а |
множества |
|
|
|
|
— областями |
внутри |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
прямоугольника. На следующем рисунке |
проиллюстрированы введённые определения |
|||||||||||||||||||||||
|
|
, , , … |
|
|
|
|
|
|
|
|||||||||||||||
операций над множествами.
Рисунок 13
Алгебрамножеств— этопримербулевойалгебры,поэтомувсеуказанныедалее(см. следующую таблицу) свойства операций следуют из свойств дизъюнкции, конъюнкции и отрицания.
Таблица 2
Свойства операций над множествами
Идемпотентность
Коммутативность
Ассоциативность
Дистрибутивность
Свойства
Свойства
Свойства дополнения
Законы поглощения
Законы де Моргана
Бинарное отношение
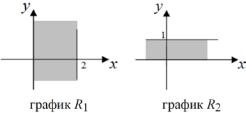
расположенных в |
|
|
|
|
|
|
( , ) |
|
|
|
|
|
|
и |
|
|
|
|
|
равны(, , ) |
|
|
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
когда |
|
|
|
|
|
|
|
. В частности, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
, |
||||||||||||||||||||||||||||||||
Упорядоченная пара |
|
|
|
|
|
|
— совокупность, |
|
состоящая из двух элементов |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
= , |
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
( , ) |
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
равны только тогда, |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
определенном порядке. Две пары |
|
|
|
|
и |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
элементов, расположенных в |
|
|
|
|
|
|
|
( , , … , ) |
|
|
если |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
— совокупность, состоящая из |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Упорядоченная |
совокупность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
множества |
|
|
|
|
|
|
|
|
|
|
|
|
|
определенном порядке. |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
называется бинарным |
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
— любое |
||||||||||||||||||||||||||||||||||||||||||||||||
Бинарное (двуместное) отношение |
|
|
из множества |
|
|
|
|
в множество |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
× |
|
|
|
|
|
|
|
|
|
произведения |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
подмножество |
|
|
|
прямого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
( , ) |
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
|
|
|
|
|
|
отношением |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на множестве . |
Если пара |
|||||||||||||||||||||||||||||||||||||||
отношения . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
принадлежит |
|
: |
|
|
|
|
|
|
|
|
|
, |
то говорят, что элемент |
|
|
|
находится в |
отношении |
|
|
|
с |
|||||||||||||||||||||||||||||||||||||||||||||
элементом |
, и записывают |
|
|
|
|
|
. Элементы |
|
|
|
|
и |
|
|
— координаты (или компоненты) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример. |
Множество |
|
|
есть |
|
множество |
|
вещественных |
|
|
чисел |
(множество точек |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вещественной |
|
|
прямой), |
. Если на |
|
|
< |
|
|
|
|
|
|
|
|
|
точек |
|
|
|
координатной |
|
|
|
|
|
|
|
= |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
— множество |
|
|
|
|
плоскости. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
{( , )| , |
: |
|
< } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяется |
|
|
|
|
множеством |
|
|
пар |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
Отношение |
|
|
строгого |
неравенства |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
есть |
|
|
|
|
< |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости выбрана декартова система координат, |
||||||||||||||||||||||||||||||||||||||||||||
то отношение |
|
|
есть множество точек, у которых абсцисса ( |
|
) меньше ординаты ( |
), то |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
тогда и только тогда, когда |
|
|
|
и |
|
|
имеют |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
множество точек, лежащих выше биссектрисы 1-го и 3-го координатных углов. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример. Введём отношение сравнимости |
|
|
|
: |
|
|
|
сравнимо с |
|
|
по модулю |
|
|
(mod. |
|
|
|
|
) |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
≡ |
|
( ). ) |
|
|
|
|
|
|
одинаковые остатки от деления на |
|
|
|
(что |
|||||||||||||||||||||||||||||||||||||||||||||||
= 3 |
|
|
|
≡ |
( . 3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
{1,2,3,4} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
случая |
||||||||||||||||||||||||||||
записывается как |
|
|
|
|
|
(1,2) |
|
|
|
|
|
). Рассмотрим отношение сравнимости для |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
(то есть |
|
(1,1) |
|
|
|
|
(1,3) |
|
(1,4) |
|
|
|
|
|
|
|
|
|
(1,1) |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
(1,4) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
× = |
|
|
(2,1) |
|
|
(2,2) |
|
|
(2,3) |
|
(2,4) |
, = |
|
|
|
|
|
(2,2) |
|
|
(3,3) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
(3,1) |
|
|
(3,2) |
|
|
(3,3) |
|
(3,4) |
(4,1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Область |
|
|
|
(4,1) |
|
|
(4,2) |
|
|
(4,3) |
|
(4,4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4,4) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Область значений |
|
|
|
|
|
|
|
= { | , |
|
: } |
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
определения бинарного отношения |
|
|
— множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: } |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= { | , |
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
бинарного отношения |
|
|
|
|
— множество |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Для |
|
= {(1,2), (2,4), (3,3), |
(2,1)}, |
= {1,2,3}, |
|
= |
{1,2,3,4} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
бинарных отношений обычным образом определены операции объединения, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
пересечения и др. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|||||||||||||
График бинарного отношения — множество точек плоскости, координаты |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на следующем рисунке.1 |
= |
{( , )|0 ≤ |
≤ |
2} |
|
|
|
|
2 |
= {( , )|0 |
≤ |
≤ 1} |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
которых образуют упорядоченные пары некоторого бинарного отношения. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример. |
Графики |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
представлены |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 14
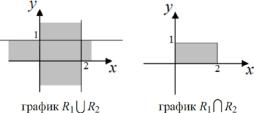
Так как бинарные1 2 отношения1 ∩ 2 — это множества, их можно объединять и пересекать. Графики и представлены на следующем рисунке.
Композиция отношений |
|
|
|
|
|
|
|
|
): |
( |
|
|
) |
|
= |
|||||||||
|
|
|
|
|
(= {( , )|( , и) |
} |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
× |
|
× |
|
|
* |
|
|
Рисунок 15 |
|||||||||
Обратное отношение для |
: |
|
|
−1 |
|
|
|
|
. Причём |
|
−1 −1 |
|
. |
|||||||||||
|
1 2 |
= |
{( , )| , , : 1 |
2 } |
|
|
|
|
|
|||||||||||||||
То есть всякая упорядоченная пара из отношения |
|
|
образовалась благодаря |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
меняются |
||||
существованию хотя бы одного элемента |
|
такого, что1 он2образует упорядоченную |
||||||||||||||||||||||
пару с элементами |
|
и |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||
местами): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
* — некоторые математики композицию обозначают иначе ( |
|
|
|
|
|
|
||||||||||||||||||
К общему |
2 1 |
= {( , )| |
, , : 1 |
2 } |
|
|
|
|
|
|||||||||||||||
|
соглашениюнасчёт обозначения композицииматематики не пришли, |
|||||||||||||||||||||||
поэтому на деле важно заранее обозначить композицию так, как будете её |
||||||||||||||||||||
Пример. |
1 = {(1, |
), (2, |
), (3, |
)}, 2 = {( , ), ( , ), |
( , )} |
|
|
|
|
|
||||||||||
использовать в дальнейшем. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Свойства 1 2 = {(1, ), (2, ), (3, )} |
|
|
|
|
|
|
|
||||||||||||
ниодин( ) |
|
|
|
бинарных отношений на множестве |
|
|||||||||||||||
Рефлексивность. Если каждый элемент множества находится в |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
антирефлексивным |
|
|
|
отношении с самим |
|||||||
собой: |
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) ¬( ) |
||||||
|
|
— то бинарное отношение называется |
рефлексивным. Если же |
|||||||||||||||||
элементмножестваненаходитсявотношенииссамимсобой: |
|
|
||||||||||||||||||
— то бинарное отношение называется |
|
|
|
|
|
. Иначе нерефлексивным. |
||||||||||||||
Пример. |
Отношение |
сравнимости рефлексивно при |
|
любом |
|
|
|
и на любом |
||||||||||||
множестве целых чисел. Отношение строгого неравенства |
|
|
( ) |
антирефлексивно. |
||||||||||||||||
|
|
|
|
|
||||||||||||||||
|
|
( , ) |
|
( |
)( ) ( ) |
|
|
|
отношении входит |
|||||||||||
Симметричность. Если вместе с каждой парой |
|
|
< > в |
|||||||||||||||||
симметричная пара |
|
|
|
: |
|
|
|
|
|
|
( —, )то бинарное отношение |
|||||||||
|
|
|
|
|
( , ) |
|
( )( ) ( |
¬ ) |
|
|
|
|||||||||
называется симметричным. Если же ни одна пара |
( , ) |
не входит в отношение вместе |
||||||||||||||||||
с симметричной парой |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
— то бинарное |
|||||
отношение называется асимметричным(полная противоположность симметричному). |
||
|
( )( ) ( ) ( = ) |
|
Если ни одна пара, состоящая из разных элементов, не входит в отношение вместе с |
||
симметричной ей: |
|
— то бинарное |
отношение называется антисимметричным. Иначе несимметричным.
Бинарное отношение асимметрично тогда и только тогда, когда оно
антисимметрично и при этом антирефлексивно. |
< |
|
> |
|
|
|
и |
||
Пример. Отношение сравнимости симметрично при любом натуральном модуле |
|
|||
на любом множестве целых чисел. Отношение строгого неравенства |
|
( |
) |
|
асимметрично на множестве вещественных чисел. Отношение нестрогого неравенства |
|||||||||||||||||||||||||||||||||||||
≤ |
( |
≥ входят |
в |
отношение |
|
, |
то в |
|
входит |
пара |
|
, , : |
|
|
|
|
|
|
|
( , ) |
|
||||||||||||||||
|
) на множестве вещественных чисел антисимметрично. |
|
|
( )( |
)( |
||||||||||||||||||||||||||||||||
( , ) |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
( , ) |
|
|||||||||||||||||||
|
Транзитивность. Если для любых трёх элементов |
|
|
|
|
|
|
|
|
|
, таких, что |
|
|
|
и |
||||||||||||||||||||||
) ( ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример. Отношение |
сравнимости |
транзитивно при |
|
любом |
|
|
|
|
и |
на |
|
любом |
||||||||||||||||||||||||
множестве целых чисел. Отношение строгого неравенства |
|
( |
|
) |
транзитивно на любом |
||||||||||||||||||||||||||||||||
< |
> |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
подмножестве |
вещественных |
|
чисел. |
Отношение |
|
|
|
|
− 3 |
на |
|
множестве |
|||||||||||||||||||||||||
|
Способы задания бинарных отношений: |
9 |
− 6 |
< 5, 6 |
< 5, 9 |
− 3 5 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
! |
|
||||||||||||||||
вещественных чисел не является транзитивным: |
|
|
|
|
|
|
| − | < 5 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2. Задание |
= {( 1, 2), ( 1 |
, 2), ( 1 |
, 2)} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1. Явное перечисление пар, определяющих бинарное отношение. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
Пример. |
|
|
|
|
|
|
|
|
|
. |
( . |
3)} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3. Задание |
= {( , )| , : ≡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
процедуры проверки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Пример. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
матрицей смежности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Диагональ матрицы смежности рефлексивного отношения состоит из единиц, |
|||||||||||||||||||||||||||||||||||
|
|
антирефлексивного — из нулей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Можно |
|
= |
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диагонали ( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Матрица смежности симметричного отношения симметрична относительно |
|||||||||||||||||||||||||||||||||||
|
|
Пример. |
|
|
|
. Пусть |
|
|
|
: если |
|
, то |
|
|
|
|
|
, иначе |
|
|
|
|
|
. ≤ |
|
|
|||||||||||
|
|
|
доказать, что для того, чтобы отношение было транзитивным, необходимо |
||||||||||||||||||||||||||||||||||
|
|
В данном = {1,2,3,4} |
|
|
|
= |
× |
|
|
|
|
|
|
|
|
|
= 1 |
|
|
|
|
= 0 |
|
. |
|
||||||||||||
|
|
и достаточно, чтобы его матрица смежности удовлетворяла неравенству |
|
2 |
|
||||||||||||||||||||||||||||||||
|
|
модулю 3 на множестве . |
|
|
|
1 |
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по |
|||||||||
|
|
|
|
|
случае приведена матрица |
смежности отношения сравнимости |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0 |
0 |
|
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0 |
|
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Как можно понять, отношение рефлексивно, симметрично и транзитивно.
Элементы множества изображаются точками плоскости и образуют множество
вершин графа. Отношения изображаются рёбрами графа: если пара |
|
|
|
входит в |
|||||||||
отношение, то из вершины проводится ориентированное ребро в |
вершину . |
||||||||||||
|
( , ) |
|
|||||||||||
Граф рефлексивного |
отношения имеет петли в каждой вершине. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Граф симметричного отношения вместе с ребром, соединяющим |
|
с |
, содержит |
||||||||||
ребро, соединяющее |
|
с . |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
отношения обладает следующим свойством: если из вершины |
|||||||||||
Граф транзитивного |
|
|
|
|
|
|
|
|
|
|
|
||
|
, двигаясь вдоль рёбер, можно попасть в вершину |
|
, то в графе должно быть |
||||||||||
ребро, непосредственно соединяющее |
|
с . |
|
|
|
|
|
|
|
||||
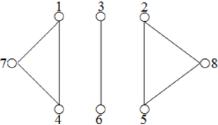
{1,2,3,4,5,6,7,8} |
|
|
{1,4,7} {3,6} |
|
{2,5,8} |
= |
|
Пример. Граф |
для отношения сравнимости по модулю 3 на множестве |
||||||
состоит из трёх компонент связности: |
, |
и |
. |
||||
|
|
|
|
|
|
|
|
Рисунок 16
Петли изображены в виде небольших окружностей.
Ориентированные рёбра заменены неориентированными рёбрами, так как отношение симметрично.
5. Задание списком смежностей.
|
Для каждого элемента множества перечисляются те элементы, которые находятся |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
с ним в данном отношении. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 → 4, 1 → 7, 2 → 5, 2 → 8, 3 → 6, 4 → 1, 4 → 7 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
Пример. Список смежности для отношения сравнимости по модулю 3 (см. пред.): |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5 → 2, 5 → 8, 6 → 3, 7 → 1, 7 → 4, 8 → 2, 8 → 5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( , 1) |
|
|
Функция |
|
|
|
1 |
. |
× |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
определен |
первый элемент |
|
( , 2) |
|
|
= 2 |
|
|
|
|
|
|
|
, |
|
обладающее |
|||||||||||||||||||||||||||||||||||||||
Функция |
|
(отображение) |
— бинарное |
|
|
отношение |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
следующим свойством: если |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
, то |
|
|
|
|
|
|
|
Это означает, что если |
|||||||||||||||||||||||||||||||
множестве |
|
со |
|
|
|
|
|
|
|
|
|
|
упорядоченной |
пары, |
|
то |
второй |
элемент |
определяется |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
: → |
|
|
|
|
= ( ) |
функции |
|
называют |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
единственным |
|
образом. |
|
Это |
|
свойство |
|
однозначностью. |
|||||||||||||||||||||||||||||||||||||||||||||||
во множество |
|
(или устанавливает |
|
|
|
|
|
|
, что означает, что функция |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
Обозначают функцию |
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
задана на |
||||||||||||||||||||||||||||||||||||||||
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
||
( ) |
|
|
|
|
|
|
значениями во множестве и осуществляет отображение множества |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
В силу |
|||||
условия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
соответствие между множествами |
|
|
|
|
). Если |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
называют аргументом функции, |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
то элемент |
|
из множества |
|
|
|
|
или прообразом |
||||||||||||||||||||||||||||||||||||||||||||||
элемента |
|
, а элемент |
|
|
|
— значением функции, |
или образом элемента . |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
однозначности у всякого прообраза имеется единственный образ. |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ( 1 |
, … , ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Аргументы функции — элементы произвольной природы, в частности, они могут |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Область определения |
|
|
функции : —→ |
|
|
= ( 1 |
, … , ) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
быть упорядоченными последовательностями |
|
|
|
|
|
|
|
|
. В этом случае функцию |
||||||||||||||||||||||||||||||||||||||||||||||
называют функцией |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
= |
{ |
| |
||||||||||||||||||
|
|
|
переменных |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
: = ( )} |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
множество её прообразов: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
. Если область определения совпадает |
с |
|
|
|
( |
|
|
|
|
|
), |
то |
|
функция |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= { ), | : = |
||||||||||||||||||
называется тотальной, в противном случае — частично определенной. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
( )} |
|
сюръективной |
|
|
|
|
|
|
— множество её образов: |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Область значений |
|
|
|
функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
. |
Если область значений совпадает с множеством |
|
|
|
( |
|
|
|
|
|
|
то функция |
||||||||||||||||||||||||||||||||||||||||
называется |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
: → |
|
|
|
|
(или, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
||||||||||
( 1)( 2)( ) = ( 1) |
|
= |
( 2) |
|
( 1 = 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1, ) |
|
|
|||||||||||||||||||||||||||||||||
Инъективное |
|
отображение. |
|
Пусть |
|
|
|
|
|
. |
Функция |
|
|
инъективна, |
если |
||||||||||||||||||||||||||||||||||||||||
( 2, ) |
|
|
|
|
|
|
|
|
1 |
= 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
из |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
иначе, |
|
|
|
|
|
|
|
||||||||
|
|
|
следует, что |
|
|
|
|
|
). То есть если у каждого образа ( |
|
) есть не болееодного |
||||||||||||||||||||||||||||||||||||||||||||
прообраза ( |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
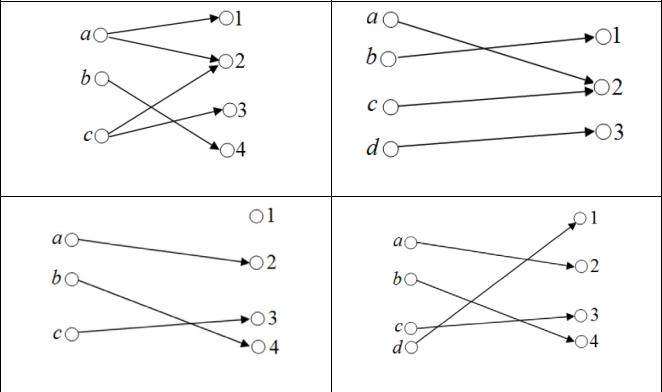
( )( ) |
|
|
|
. То есть если у |
|
|
: |
→ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= ( ) |
|
|
|
|
|
|
. |
Функция |
|
сюръективна, |
||||||||||||||
Сюръективное отображение. Пусть |
|
|
|
|
|
если |
||||||||||||||||||
одновременно |
инъективна и |
|
каждого образа ( |
|
) есть хотя бы один прообраз ( ). |
|||||||||||||||||||
|
|
: → |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||
Говорят, что такая функция отображает множество |
|
на множество |
|
|
|
|
|
|||||||||||||||||
Биективное |
отображение. |
Пусть |
|
|
|
. |
Функция |
|
|
|
|
|
|
если |
она |
|||||||||
Примеры. ( |
|
) |
|
|
|
|
|
|
|
|
|
|
биективна, |
|||||||||||
|
сюръективна. |
|
То |
есть |
|
|
|
|
|
|
|
|
взаимно |
|||||||||||
|
|
|
: → |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и . |
|
|
|
||
однозначное (один к одному) соответствие между двумя множествами |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1 |
( ) = |
|
− |
— сюръективна, но не инъективна ( |
|
|
|
|
|
|
|
|
). |
|
||||||||||
2 |
( ) = |
3 |
— биективна. |
|
|
|
|
|
|
|
= (−1 или 1) = 0 |
|
|
|||||||||||
|
|
|
— инъективна, но не сюръективна (так как всегда выше оси ). |
|
|
|
||||||||||||||||||
3( ) = 2 + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Бинарное отношение, но не функция |
Сюръекция, но не инъекция |
|
Инъекция, но не сюръекция |
Тотальная биекция |
|
|
||
Отображение, при |
|
|
|
|
17 |
|
|
|
|
|
|
Рисунок |
|
|
Пример. Пусть |
|
— множество пальто в |
гардеробе, — множество крючков. |
||
котором каждому пальто сопоставляется крючок, на котором оно висит, является инъективным, если на каждом крючке висит не более одного пальто (некоторые крючкимогут быть пустыми). Отображение является сюръективным, если на каждом крючке висит хотя бы одно пальто (на некоторых крючках может быть несколько пальто). Отображение является биективным, если на каждом крючке висит
ровно одно пальто. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
элементов, |
|
|
|
|
|
конечного множества |
|
в |
|
|
|||||
Если существует биективное |
отображение |
|
конечное |
||||||||||||
множество |
|
|
, то в множествах |
|
и поровну элементов. Если в |
множестве |
|
больше |
|||||||
|
|
|
|
|
|
|
|
|
|||||||
Так как функция — бинарное |
|
|
|
|
|
|
|
|
|
||||||
|
чемвмножестве , тонесуществуетинъективногоотображения |
|
в . Если |
||||||||||||
существует сюръективное |
отображение |
|
в , то в не меньше элементов, чем в . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
быть |
|
|
|
|
|
отношение, то можно построить обратное бинарное |
|||||||||
отношение |
|
−, котороенеобязательнобудетфункцией.Условиеоднозначностиможет |
|||||||||||||
нарушено.
