- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
Бинарная
алгебраическая операция (или закон
композиции) на непустом множестве
 — отображение множества всех
упорядоченных пар
— отображение множества всех
упорядоченных пар
 в множество
в множество
 объектов любой природы. При этом если
упорядоченной паре
объектов любой природы. При этом если
упорядоченной паре
 ,
где
,
где
 ,
ставится в соответствие элемент
,
ставится в соответствие элемент
 ,
то пишут
,
то пишут
 и
и
 называют бинарной операцией на множестве
называют бинарной операцией на множестве
 ,
а совокупность двух объектов
,
а совокупность двух объектов
 называют алгебраической системой
с основным множеством
называют алгебраической системой
с основным множеством
 и бинарной операцией
и бинарной операцией
 .
Причём говорят, что операция
.
Причём говорят, что операция
 определяет на
определяет на
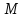 алгебраическую структуру. Тот факт,
что
алгебраическую структуру. Тот факт,
что
 обязательно принадлежит множеству
обязательно принадлежит множеству
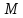 ,
называется замкнутостью структуры
по отношению к этой операции. Далее,
если не оговорено противное, мы будем
считать все рассматриваемые бинарные
операции замкнутыми.
,
называется замкнутостью структуры
по отношению к этой операции. Далее,
если не оговорено противное, мы будем
считать все рассматриваемые бинарные
операции замкнутыми.
Все алгебраические структуры с одним набором операций можно классифицировать следующим образом:
-
Простые алгебраические структуры (бинарных операций нет):
-
Множество.
-
Множество с отмеченной точкой.
-
Некоторые другие…
-
-
Группообразные структуры (одна бинарная операция).
-
Магма.
-
Полугруппа.
-
Моноид.
-
Группа.
-
Полурешётка.
-
Некоторые другие…
-
-
Кольцеобразные структуры (две бинарные операции: сложение и умножение).
-
Полукольцо.
-
Почтикольцо.
-
Кольцо.
-
Область целостности.
-
Поле.
-
Некоторые другие…
-
-
Решётчатые структуры (две или более бинарные операции).
-
Полная решётка.
-
Булева алгебра.
-
Некоторые другие…
-
-
Арифметика (две бинарные операции: сложение и умножение, бесконечные множества).
-
Арифметика Робинсона.
-
Арифметика Пеано.
-
Мы рассмотрим 6 следующих структур: 3 с одной бинарной операцией — полугруппы, моноиды и группы; 3 с двумя бинарными операциями — кольца, области целостности и поля.
Подструктура
данной алгебраической структуры —
подмножество множества
—
подмножество множества
 ,
само являющееся структурой с теми же
структурными операциями.
,
само являющееся структурой с теми же
структурными операциями.
Пример. Подполугруппа — подмножество полугруппы, само являющееся полугруппой, подмоноид — подмножество моноида, само являющееся моноидом, подгруппа — подмножество группы, само являющееся группой.
Каждая структура содержит:
-
Несобственные подструктуры: сама структура и нейтральный элемент
 (см. далее).
(см. далее). -
Собственные подструктуры: все остальные подструктуры (то есть те, которые не являются несобственными).
Пример.
Множество
 .
Его несобственные подмножества:
.
Его несобственные подмножества:
 (
( — означает пустое множество); собственные:
— означает пустое множество); собственные:
 .
По такой аналогии можно понимать и
подструктуры алгебраических структур.
.
По такой аналогии можно понимать и
подструктуры алгебраических структур.
Символы:
-
 — квантор всеобщности.
— квантор всеобщности.
 — для любого (всякого, каждого) значения
— для любого (всякого, каждого) значения
 из
из
 :
:
 истинно.
истинно. -
 — квантор существования.
— квантор существования.
 — существует (найдётся) значение
— существует (найдётся) значение
 из
из
 такое, что
такое, что
 истинно.
истинно.
 — существует и единственный.
— существует и единственный. -
 — отрицание.
— отрицание.
 — для любого (всякого, каждого) значения
— для любого (всякого, каждого) значения
 из
из
 :
:
 не истинно (ложно).
не истинно (ложно).
 — существует (найдётся) значение
— существует (найдётся) значение
 из
из
 такое, что
такое, что
 не истинно (ложно).
не истинно (ложно). -
 — символ сложения. Результат называется
суммой.
— символ сложения. Результат называется
суммой. -
 — символ вычитания. Результат называется
разностью.
— символ вычитания. Результат называется
разностью. -
 — символ умножения. Результат называется
произведением.
— символ умножения. Результат называется
произведением. -
 — символ деления. Результат называется
частным (возможно с остатком).
— символ деления. Результат называется
частным (возможно с остатком). -
 — символы произвольных различных
бинарных операций.
— символы произвольных различных
бинарных операций.
Числа:
-
 — натуральные числа.
— натуральные числа. -
 — натуральные числа с нулём.
— натуральные числа с нулём. -
 — чётные натуральные числа. Также с
нулём:
— чётные натуральные числа. Также с
нулём:

-
 — целые числа. Коротко:
— целые числа. Коротко:
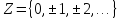 .
. -
 — чётные целые числа.
— чётные целые числа. -
 — целые числа без нуля.
— целые числа без нуля. -
 — положительные целые числа.
— положительные целые числа. -
 — отрицательные целые числа.
— отрицательные целые числа. -
 — целые числа по модулю
— целые числа по модулю
 .
. -
 — рациональные числа (наивное
определение).
— рациональные числа (наивное
определение). -
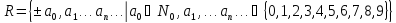 — вещественные (действительные) числа
(неполное определение).
— вещественные (действительные) числа
(неполное определение).
 — положительные и отрицательные
вещественные числа с нулями.
— положительные и отрицательные
вещественные числа с нулями. -
 — комплексные числа (неполное
определение).
— комплексные числа (неполное
определение).
Пример.

 — чётно.
— чётно.
 — ложно (не любое натуральное чётно).
— ложно (не любое натуральное чётно).
Пример.

 — чётно.
— чётно.
 — истинно (любое чётное целое чётно).
— истинно (любое чётное целое чётно).
Пример.

 — чётно.
— чётно.
 — истинно (найдётся чётное натуральное).
— истинно (найдётся чётное натуральное).
Пример.

 — чётно.
— чётно.
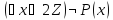 — ложно (не найдётся нечётное среди
чётных).
— ложно (не найдётся нечётное среди
чётных).
Пример.
Вычитание, определённое на множестве
 ,
— незамкнутая операция, так как
,
— незамкнутая операция, так как
 ,
а сложение — замкнутая:
,
а сложение — замкнутая:
 .
.
Замкнутость
множества
 относительно операции:
относительно операции:

Ассоциативность
операции
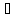 (сочетательный закон):
(сочетательный закон):

Коммутативность
операции
 (переместительный закон):
(переместительный закон):

Дистрибутивность
операции
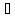 относительно
относительно
 (распределительный закон):
(распределительный закон):
(слева)

(справа)

Если
операция
 является коммутативной, то свойства
дистрибутивности слева и справа
равносильны.
является коммутативной, то свойства
дистрибутивности слева и справа
равносильны.
Обратим
внимание на то, что коммутативность и
ассоциативность независимы. Например,
в множестве
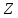 операция:
операция:
 — коммутативна, но не ассоциативна, так
как:
— коммутативна, но не ассоциативна, так
как:

Магма
Магма
— множество
 с одной бинарной операцией
с одной бинарной операцией
 .
Помимо требования замкнутости множества
относительно заданной на нём операции,
других требований к операции и множеству
не предъявляется.
.
Помимо требования замкнутости множества
относительно заданной на нём операции,
других требований к операции и множеству
не предъявляется.
Магма не часто изучается как таковая; вместо этого существует несколько различных типов магмы, в зависимости от того, каким аксиомам операция должна удовлетворять.
В следующей таблице представлена классификация алгебраических структур с одной бинарной операцией по свойствам (просто для получения общей картины).
 означает, что свойство (аксиома)
присутствует (обязательно соблюдается).
означает, что свойство (аксиома)
присутствует (обязательно соблюдается).
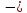 означает, что свойство (аксиома)
отсутствует (может соблюдаться, а может
и не соблюдаться).
означает, что свойство (аксиома)
отсутствует (может соблюдаться, а может
и не соблюдаться).
Таблица 3
|
Название |
Замкнутость |
Ассоциативность |
Нейтральный
элемент
|
Обратимость
|
Коммутативность |
|
Полугруппоид (теория категорий) |
|
|
|
|
|
|
Малая категория (теория категорий) |
|
|
|
|
|
|
Группоид (теория категорий) |
|
|
|
|
|
|
Магма |
|
|
|
|
|
|
Квазигруппа |
|
|
|
|
|
|
Полугруппа |
|
|
|
|
|
|
Моноид |
|
|
|
|
|
|
Группа |
|
|
|
|
|
|
Абелева группа |
|
|
|
|
|
Как видим, в магме есть только замкнутость, значит те структуры, которые обладают замкнутостью, магма обобщает:
Магма
 Полугруппа
Полугруппа
 Моноид
Моноид
 Группа
Группа
 Абелева группа.
Абелева группа.
То есть всякая абелева группа — это магма, всякая группа — это тоже магма и т. д. (Всякая группа — это моноид, всякий моноид — это полугруппа…)
Нейтральный элемент и обратимость будут описаны позже.