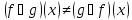- •По дискретной математике
- •0. Введение. Граф
- •Виды графов
- •Основная информация
- •Матрицы
- •1. Сеть. Потоки в сети. Теорема Форда — Фалкерсона
- •2. Функция. Бинарное отношение. Тотальность, сюръективность, инъективность, биективность. Примеры Множество
- •Бинарное отношение
- •Свойства бинарных отношений на множестве
- •Явное перечисление пар, определяющих бинарное отношение.
- •Задание процедуры проверки.
- •Задание матрицей смежности.
- •Задание графом.
- •Задание списком смежностей.
- •Функция
- •3. Бинарное отношение. Свойства. Матрица смежности и граф отношения. Отношение эквивалентности. Примеры
- •Отношение эквивалентности
- •4. Множество точек любой прямой имеет мощность континуума.
- •4. Алгебраическая структура. Полугруппа, моноид, группа. Примеры
- •Полугруппа
- •5. Группа. Абелева группа. Аддитивная группа. Мультипликативная группа. Конечная группа. Таблица Кэли. Циклическая группа. Декартово произведение групп Группа
- •Циклическая группа
- •Декартово произведение групп
- •6. Группа подстановок. Симметрическая группа . Умножение подстановок. Нейтральный элемент. Обратная подстановка. Число элементов группы Группа подстановок
- •7. Цикл. Теорема о представлении подстановки в виде произведения независимых циклов. Транспозиция. Чётные и нечётные подстановки. Знакопеременная группа Цикл
- •Гомоморфизм. Изоморфизм. Теорема Кэли
- •8. Кольцо. Свойства. Коммутативное кольцо. Делители 0. Область целостности. Примеры. Подкольцо. Единица кольца. Поле. Примеры Кольцо
- •9. Идеал. Главный идеал. Теорема об идеалах поля (только и ). Следствие об идеалах в кольце Идеал
- •10. Сравнения. Классы вычетов по модулю (по идеалу ). Свойства. Малая теорема Ферма. Функция Эйлера. Теорема Эйлера (теория чисел) Сравнения
- •Свойства сравнений
- •11. Характеристика кольца. Теорема о характеристике кольца без делителей 0. Примеры. Кольцо классов вычетов. Примеры Характеристика кольца
- •12. Простой идеал. Необходимое и достаточное условие того, что идеал кольца — простой Простой идеал
- •13. Поле классов вычетов. Минимальное поле. Примеры Поле классов вычетов
- •14. Евклидово кольцо. Свойства (8 свойств). Примеры Евклидово кольцо
- •Свойства евклидовых колец
- •В евклидовом кольце все идеалы главные.
- •Любое евклидово кольцо содержит 1.
- •Если в евклидовом кольце ( делит ), но не делит , то .
- •15. Кольцо многочленов . Условия того, что кольцо — евклидово кольцо Кольцо многочленов
- •16. Приводимые и неприводимые многочлены в кольце . Примеры. Теорема о разложении в на произведение неприводимых множителей. Теорема Безу
- •17. Расширение поля (надполе). Теорема о том, что кольцо классов вычетов по модулю неприводимого многочлена есть поле. Степень расширения. Число элементов этого поля Расширение поля
- •18. Поле Галуа. Примеры полей Галуа как расширения полей. Таблицы сложения и умножения Поле Галуа
- •Литература
-
Явное перечисление пар, определяющих бинарное отношение.
Пример.
 .
.
-
Задание процедуры проверки.
Пример.
 .
.
-
Задание матрицей смежности.
Диагональ матрицы смежности рефлексивного отношения состоит из единиц, антирефлексивного — из нулей.
Матрица смежности симметричного
отношения симметрична относительно
диагонали ( ).
).
Можно доказать, что для того, чтобы
отношение было транзитивным, необходимо
и достаточно, чтобы его матрица смежности
удовлетворяла неравенству
 .
.
Пример.
 .
Пусть
.
Пусть
 :
если
:
если
 ,
то
,
то
 ,
иначе
,
иначе
 .
.
В данном случае приведена матрица
смежности отношения сравнимости по
модулю 3 на множестве
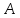 .
.

Как можно понять, отношение рефлексивно, симметрично и транзитивно.
-
Задание графом.
Элементы множества изображаются точками
плоскости и образуют множество вершин
графа. Отношения изображаются рёбрами
графа: если пара
 входит в отношение, то из вершины
входит в отношение, то из вершины
 проводится ориентированное ребро в
вершину
проводится ориентированное ребро в
вершину
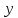 .
.
Граф рефлексивного отношения имеет петли в каждой вершине.
Граф симметричного отношения вместе с
ребром, соединяющим
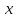 с
с
 ,
содержит ребро, соединяющее
,
содержит ребро, соединяющее
 с
с
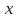 .
.
Граф транзитивного отношения обладает
следующим свойством: если из вершины
 ,
двигаясь вдоль рёбер, можно попасть в
вершину
,
двигаясь вдоль рёбер, можно попасть в
вершину
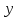 ,
то в графе должно быть ребро, непосредственно
соединяющее
,
то в графе должно быть ребро, непосредственно
соединяющее
 с
с
 .
.
Пример. Граф для отношения
сравнимости по модулю 3 на множестве
 состоит из трёх компонент связности:
состоит из трёх компонент связности:
 ,
,
 и
и
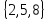 .
.

Рисунок 16
Петли изображены в виде небольших окружностей.
Ориентированные рёбра заменены неориентированными рёбрами, так как отношение симметрично.
-
Задание списком смежностей.
Для каждого элемента множества перечисляются те элементы, которые находятся с ним в данном отношении.
Пример. Список смежности для отношения сравнимости по модулю 3 (см. пред.):


Функция
Функция
(отображение) — бинарное отношение
 ,
обладающее следующим свойством: если
,
обладающее следующим свойством: если
 и
и
 ,
то
,
то
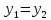 .
Это означает, что если определен первый
элемент упорядоченной пары, то второй
элемент определяется единственным
образом. Это свойство функции называют
однозначностью. Обозначают функцию
.
Это означает, что если определен первый
элемент упорядоченной пары, то второй
элемент определяется единственным
образом. Это свойство функции называют
однозначностью. Обозначают функцию
 или
или
 ,
что означает, что функция
,
что означает, что функция
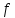 задана на множестве
задана на множестве
 со значениями во множестве
со значениями во множестве
 и осуществляет отображение множества
и осуществляет отображение множества
 во множество
во множество
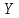 (или устанавливает соответствие между
множествами
(или устанавливает соответствие между
множествами
 и
и
 ).
Если
).
Если
 ,
то элемент
,
то элемент
 из множества
из множества
 называют аргументом функции, или
прообразом элемента
называют аргументом функции, или
прообразом элемента
 ,
а элемент
,
а элемент
 — значением функции, или образом элемента
— значением функции, или образом элемента
 .
В силу условия однозначности у всякого
прообраза имеется единственный образ.
.
В силу условия однозначности у всякого
прообраза имеется единственный образ.
Аргументы
функции — элементы произвольной
природы, в частности, они могут быть
упорядоченными последовательностями
 .
В этом случае функцию
.
В этом случае функцию
 называют функцией
называют функцией
 переменных
переменных
 или
или
 .
.
Область
определения
 функции
функции
 — множество её прообразов:
— множество её прообразов:
 .
Если область определения совпадает с
.
Если область определения совпадает с
 (
( ),
то функция называется тотальной, в
противном случае — частично определенной.
),
то функция называется тотальной, в
противном случае — частично определенной.
Область
значений
 функции
функции
 — множество её образов:
— множество её образов:
 .
Если область значений совпадает с
множеством
.
Если область значений совпадает с
множеством
 (
( ),
то функция называется сюръективной.
),
то функция называется сюръективной.
Инъективное
отображение. Пусть
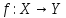 .
Функция
.
Функция
 инъективна, если
инъективна, если
 (или, иначе, из
(или, иначе, из
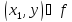 и
и
 следует, что
следует, что
 ).
То есть если у каждого образа (
).
То есть если у каждого образа ( )
есть не более одного прообраза (
)
есть не более одного прообраза ( ).
).
Сюръективное
отображение. Пусть
 .
Функция
.
Функция
 сюръективна, если
сюръективна, если
 .
То есть если у каждого образа (
.
То есть если у каждого образа ( )
есть хотя бы один прообраз (
)
есть хотя бы один прообраз (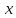 ).
Говорят, что такая функция отображает
множество
).
Говорят, что такая функция отображает
множество
 на множество
на множество
 .
.
Биективное
отображение. Пусть
 .
Функция
.
Функция
 биективна, если она одновременно
инъективна и сюръективна. То есть
биективна, если она одновременно
инъективна и сюръективна. То есть
 осуществляет взаимно однозначное
(один к одному) соответствие между
двумя множествами
осуществляет взаимно однозначное
(один к одному) соответствие между
двумя множествами
 и
и
 .
.
Примеры.
(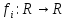 )
)
 — инъективна, но не сюръективна (так
как всегда выше оси
— инъективна, но не сюръективна (так
как всегда выше оси
 ).
).
 — сюръективна, но не инъективна (
— сюръективна, но не инъективна ( ).
).
 — биективна.
— биективна.
|
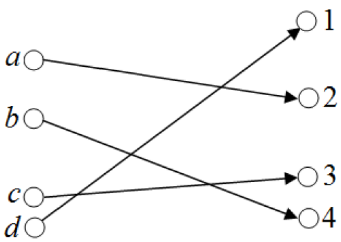
Бинарное отношение, но не функция |
Сюръекция, но не инъекция |
|
Инъекция, но не сюръекция |
Тотальная биекция |
Рисунок 17
Пример.
Пусть
 — множество пальто в гардеробе,
— множество пальто в гардеробе,
 — множество крючков. Отображение, при
котором каждому пальто сопоставляется
крючок, на котором оно висит, является
инъективным, если на каждом крючке
висит не более одного пальто (некоторые
крючки могут быть пустыми). Отображение
является сюръективным, если на
каждом крючке висит хотя бы одно пальто
(на некоторых крючках может быть несколько
пальто). Отображение является биективным,
если на каждом крючке висит ровно одно
пальто.
— множество крючков. Отображение, при
котором каждому пальто сопоставляется
крючок, на котором оно висит, является
инъективным, если на каждом крючке
висит не более одного пальто (некоторые
крючки могут быть пустыми). Отображение
является сюръективным, если на
каждом крючке висит хотя бы одно пальто
(на некоторых крючках может быть несколько
пальто). Отображение является биективным,
если на каждом крючке висит ровно одно
пальто.
Если
существует биективное отображение
конечного множества
 в конечное множество
в конечное множество
 ,
то в множествах
,
то в множествах
 и
и
 поровну элементов. Если в множестве
поровну элементов. Если в множестве
 больше элементов, чем в множестве
больше элементов, чем в множестве
 ,
то не существует инъективного отображения
,
то не существует инъективного отображения
 в
в
 .
Если существует сюръективное отображение
.
Если существует сюръективное отображение
 в
в
 ,
то в
,
то в
 не меньше элементов, чем в
не меньше элементов, чем в
 .
.
Так
как функция — бинарное отношение, то
можно построить обратное бинарное
отношение
 ,
которое не обязательно будет функцией.
Условие однозначности может быть
нарушено.
,
которое не обязательно будет функцией.
Условие однозначности может быть
нарушено.
Пример.
На множестве вещественных чисел
 задано отношение
задано отношение
 — функция. Но обратное отношение
— функция. Но обратное отношение
 уже функцией не является, так как ему,
например, принадлежат пары
уже функцией не является, так как ему,
например, принадлежат пары
 и
и
 .
.
Чтобы
условие однозначности выполнялось для
 ,
функция должна быть биективной. (Если
функция будет инъективной, то может не
найтись какой-нибудь
,
функция должна быть биективной. (Если
функция будет инъективной, то может не
найтись какой-нибудь
 для
для
 ,
а если будет сюръективной, то могут
найтись два или более
,
а если будет сюръективной, то могут
найтись два или более
 для
для
 .)
.)
Так как всякая функция — бинарное отношение, то композиция функций строится как композиция бинарных отношений.
Пусть
 и
и
 .
Их композиция определяется обычным
образом:
.
Их композиция определяется обычным
образом:


Рисунок 18
Вместо
« »
некоторые пишут «
»
некоторые пишут « ».
На деле же математики, как ни странно,
не могут, да и не пытаются, прийти к
общему соглашению относительно этого
обозначения. Поэтому важно заранее
обозначить композицию так, как будете
её использовать в дальнейшем.
».
На деле же математики, как ни странно,
не могут, да и не пытаются, прийти к
общему соглашению относительно этого
обозначения. Поэтому важно заранее
обозначить композицию так, как будете
её использовать в дальнейшем.
Композиция
взаимно однозначных функций — взаимно
однозначная функция, при этом
 .
.
Пример.
Пусть
 ,
тогда
,
тогда


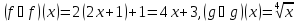
Из примера видно, что композиция — некоммутативная операция: