Бинарное отношение

Упорядоченная пара — совокупность, состоящая из двух элементов и , расположенных в определенном порядке. Две пары и равны только тогда, когда . В частности, и равны, если .

Упорядоченная совокупность — совокупность, состоящая из элементов, расположенных в определенном порядке.

Бинарное (двуместное) отношение из множества в множество — любое подмножество прямого произведения . Если , то подмножество множества называется бинарным отношением на множестве . Если пара принадлежит : , то говорят, что элемент находится в отношении с элементом , и записывают 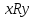. Элементы и — координаты (или компоненты) отношения .

Пример. Множество есть множество вещественных чисел (множество точек вещественной прямой), 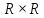— множество точек координатной плоскости. Отношение строгого неравенства определяется множеством пар . Если на плоскости выбрана декартова система координат, то отношение есть множество точек, у которых абсцисса () меньше ординаты (), то есть множество точек, лежащих выше биссектрисы 1-го и 3-го координатных углов.

Пример. Введём отношение сравнимости : сравнимо с по модулю (mod. ) тогда и только тогда, когда и имеют одинаковые остатки от деления на 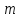(что записывается как ). Рассмотрим отношение сравнимости для случая (то есть ) на множестве :

Область определения бинарного отношения — множество :

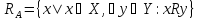
Область значений бинарного отношения — множество :

Пример. .

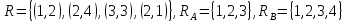Для бинарных отношений обычным образом определены операции объединения, пересечения и др.

График бинарного отношения — множество точек плоскости, координаты которых образуют упорядоченные пары некоторого бинарного отношения.

Пример. Графики и представлены на следующем рисунке.

Рисунок 14

Так как бинарные отношения — это множества, их можно объединять и пересекать.

Графики и представлены на следующем рисунке.

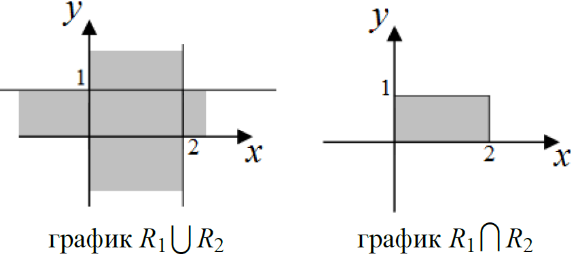
Рисунок 15

Обратное отношение для : . Причём .

Композиция отношени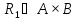й ( и ):

*

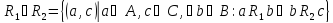То есть всякая упорядоченная пара из отношения образовалась благодаря существованию хотя бы одного элемента такого, что он образует упорядоченную пару с элементами и .

* — некоторые математики композицию обозначают иначе ( и меняются местами):

К общему соглашению насчёт обозначения композиции математики не пришли, поэтому на деле важно заранее обозначить композицию так, как будете её использовать в дальнейшем.

Пример.

Свойства бинарных отношений на множестве

Рефлексивность. Если каждый элемент множества находится в отношении с самим собой: — то бинарное отношение называется рефлексивным. Если же ни один элемент множества не находится в отношении с самим собой: — то бинарное отношение называется антирефлексивным. Иначе нерефлексивным.

Пример. Отношение сравнимости рефлексивно при любом 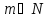и на любом множестве целых чисел. Отношение строгого неравенства () антирефлексивно.

Симметричность. Если вместе с каждой парой в отношении входит симметричная пара : — то бинарное отношение называется симметричным. Если же ни одна пара не входит в отношение вместе с симметричной парой 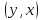: — то бинарное отношение называется асимметричным (полная противоположность симметричному). Если ни одна пара, состоящая из разных элементов, не входит в отношение вместе с симметричной ей: — то бинарное отношение называется антисимметричным. Иначе несимметричным.

Бинарное отношение асимметрично тогда и только тогда, когда оно антисимметрично и при этом антирефлексивно.

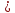Пример. Отношение сравнимости симметрично при любом натуральном модуле и на любом множестве целых чисел. Отношение строгого неравенства () асимметрично на множестве вещественных чисел. Отношение нестрогого неравенства () на множестве вещественных чисел антисимметрично.

Транзитивность. Если для любых трёх элементов , таких, что и входят в отношение , то в входит пара : .

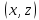Пример. Отношение сравнимости транзитивно при любом и на любом множестве целых чисел. Отношение строгого неравенства () транзитивно на любом подмножестве вещественных чисел. Отношение на множестве вещественных чисел не является транзитивным: !

Способы задания бинарных отношений: